Finite Automata In TOC
Finite Automata (FA) is an abstract machine in TOC that accepts all the regular languages. It operates with:
- A finite set of states
- A finite input alphabet (Σ)
Transition rules are used to determine movement from one state to another based on input symbols. If, after consuming the entire input, the machine ends in an accepting (final) state, the string is accepted by the FA.
Key Characteristics of FA
- Operates on a finite input alphabet (Σ)
- Has a finite set of states (Q)
- Contains one start state
- In terms of DFA and NFA, it may include one or more final/accepting states and accepts a string if it ends in an accepting state
- Uses a transition function (δ) to move from one state to another
- Processes input one symbol at a time
Symbols Table in Finite Automata
Symbols Table in Finite Automata with descriptions and a simple example is given below
| Symbol | Description | Example |
|---|---|---|
| Q | Set of all possible states in the automaton | Q = {q0, q1, q2} |
| Σ (Sigma) | Set of valid input symbols (alphabet) | Σ = {0, 1} |
| δ | Transition function: tells next state from input | δ(q0, 1) = q1 → from q0, input 1 leads to q1 |
| q₀ | Start state where the machine begins | q₀ = q0 |
| F | Set of accepting/final states (used in DFA and NFA) | F = {q2} |
| ε | Empty input symbol (used in ε-NFA, no input consumed) | δ(q1, ε) = {q2} → jump from q1 to q2 without input |
| λ (lambda) | Output function (used in Moore/Mealy machines) | In Moore: λ(q1) = 1 → state q1 gives output 1 |
Working Of Finite Automata
Every Finite automata takes a language as input, processes it through some automata machines, and gives an output in the form of a set of states. The following descriptive diagram

- For each string w ∈ L, the automaton must end in an accepting (final) state
- If all strings of a language are accepted by a finite automata machine, then it is said to be a regular language.
Flowchart of Finite Automata in TOC
To determine whether a language L is regular or not, first draw a finite automaton (FA). If the language is accepted by the FA, it is regular; otherwise, it is not regular. A simple flowchart of FA is given below

Types Of Finite Automata in TOC
There are 5 major types of finite automata, which are categorized under finite automata with output and finite automata without output
- Deterministic Finite Automata (DFA)
- Nondeterministic Finite Automata (NFA)
- Epsilon-NFA (ε-NFA)
- Moore Machine
- Mealy Machine
Following figure shows it

All five types are similar except transition function and output behavior. The following table illustrates it
Main Differences in the Transition Function (δ) and Output
| Machine Type | Transition Function (δ) | Output Type |
|---|---|---|
| DFA | δ: Q × Σ → Q | Accept/Reject |
| NFA | δ: Q × Σ → 2^Q | Accept/Reject |
| ε-NFA | δ: Q × (Σ ∪ {ε}) → 2^Q | Accept/Reject |
| Moore Machine | δ: Q × Σ → Q λ: Q → Output |
Outputs on states where Output depends only on current state |
| Mealy Machine | δ: Q × Σ → Q λ: Q × Σ → Output |
Outputs on transitions where the Output depends on the state and input |
Let’s explain each type of Finite Automata in detail
1. Deterministic Finite Automata (DFA)
One input symbol leads to only one next state.
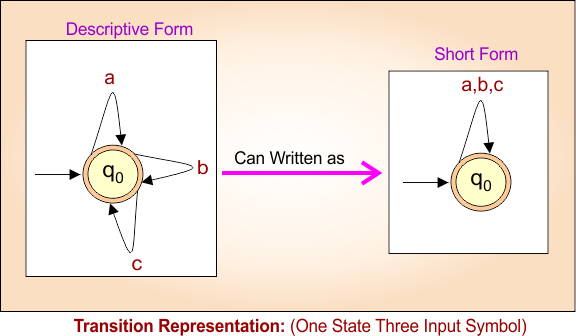
- 1 state, 2 symbols → Total possible transitions: 1×2 = 2
- 2 states, 2 symbols → Total possible transitions: 2×2 = 4
- 2 states, 3 symbols → Total possible transitions: 2×3 = 6
Some more examples in the following diagram

Important: A null (ε) move is not allowed. It means the state cannot change without an input symbol.
2. Non deterministic Finite Automata (NFA)
In NFA, a particular input symbol, the machine can move to any number of next states (including zero, one, or more).
NFA Example

NFA Transition Function is.
δ: Q X Σ → 2 ^ Q.
Explained: δ: Q X Σ → 2 ^ Q.
|
3. Epsilon NFA (ε-NFA)
Epsilon NFA is a special type of NFA where transitions can occur without consuming input. It means ε-transitions allow moving from one state to another “freely”
Epsilon-NFA Diagram is given below

-
NFA: Every transition must occur using an input symbol from Σ
-
ε-NFA: Every transition can occur using an input symbol from Σ or using epsilon (ε).
Epsilon-NFA Transition Function is
δ: Q × (Σ ∪ {ε}) → 2^Q
4. Moore Machine
In Moore Machine, the output depends only on the current state. Every state has a fixed output.
Moore Machine Diagram
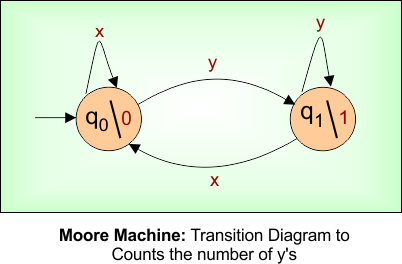
Transition Function (δ: Q × Σ → Q)
- Takes the current state and input symbol as input.
- Tells the next state to move to.
- Controls how the machine transitions between states.
- Example: δ(q0, a) = q1 → from q0, input ‘a’ goes to q1.
Output Function (λ: Q → Δ)
- Takes only the current state as input.
- Returns the output symbol for that state.
- Output depends only on the state, not the input.
- Example: λ(q1) = 1 → state q1 always outputs 1.
5 Mealy Machine
In a Mealy Machine, the output depends on both the current state and the input symbol.
Mealy Machine Diagram
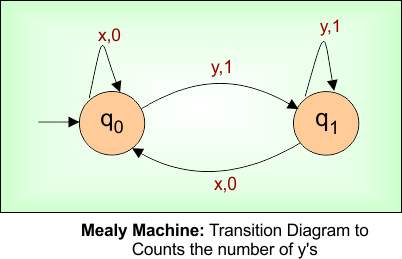
Transition Function (δ: Q × Σ → Q)
- Takes the current state and input symbol.
- Tells the next state to go to.
- Controls movement between states.
- Example: δ(q0, a) = q1 → from q0, input ‘a’ leads to q1.
Output Function (λ: Q × Σ → Δ)
- Takes the current state and input symbol.
- Returns the output for that combination.
- Output depends on state and input, not just state.
- Example: λ(q0, a) = 1 → in q0, input ‘a’ gives output 1.
Conversion between Finite Automata Types
| From / To | DFA | NFA | ε-NFA | Moore Machine | Mealy Machine |
|---|---|---|---|---|---|
| DFA | Already DFA | DFA ⊆ NFA | DFA ⊆ ε-NFA | Not directly | Not directly |
| NFA | Convert using subset method | Already NFA | Add ε-transitions if needed | Not directly | Not directly |
| ε-NFA | Remove ε, then convert to DFA | Remove ε to get NFA | Already ε-NFA | Not directly | Not directly |
| Moore | Not directly | Not directly | Not directly | Already Moore Machine | Can be converted to Mealy |
| Mealy | Not directly | Not directly | Not directly | Can be converted to Moore | Already Mealy Machine |
Summary of Conversions
- NFA to DFA Conversion: Use the subset construction method (also called powerset construction).
- ε-NFA to NFA Conversion: Eliminate ε-transitions first. It becomes NFA, Now easily converted to DFA.
- Moore to Mealy Conversion: Can be converted into each other with state expansion if needed.
- Mealy to Moore Conversion: Can be converted into each other with state expansion if needed.
- DFA/NFA/ε-NFA ↛ Moore/Mealy Conversion: Cannot be directly converted, because Moore and Mealy machines produce output, while DFA/NFA accept/reject inputs.
Applications of Finite Automata
Finite Automata are the simplest model among all computational models and serves as the foundation for compilers, lexical analyzers, and text pattern matching tools.
- Lexical Analysis in Compilers
- Text editors (e.g., syntax highlighting)
- Search engines (pattern matching)
- Digital circuit design
- Network protocol validation
- Game development (AI decision systems)
Advantages of Finite Automata
- Easy to design and implement
- Efficient string processing
- Helps in compiler construction
- Theoretical backbone for Regular Expressions
Limitations of Finite Automata
- Cannot count unlimited characters (e.g., balanced parentheses)
- Only suitable for regular languages
- Cannot model context-free or context-sensitive languages
Finite Automata Questions
Q1. Is DFA more powerful than NFA?
No. DFA and NFA are equivalent in terms of language recognition capability.
Q2. Can finite automata accept palindromes?
No, palindromes require memory beyond finite states — they are not regular.
Q3. What is a dead state in DFA?
A state from which no accepting state can be reached; often used to trap invalid strings.













