Rightmost Derivation in Automata

Getting a string by expanding the rightmost non terminal at each step is known as rightmost derivation in Automata.

• The representation of rightmost derivation in the form of tree is called as a rightmost derivation tree.
• In the rightmost derivation tree, we read the given input string (W) from left to right also.

Example of Rightmost Derivation

Consider the following production rules of a Grammar (G)

S → xB / yA

S → xS / yAA / x

B → yS / xBB / y

Consider a string W = xxxyyxyyyx

Let us derive the given string (W= xxxyyxyyyx) by using given production rules of grammar. And will also draw the derivation tree of each step as given below

Rightmost Derivation and Tree

Let us see derivation through production rules and their tree as given below

Step 01: S   → xB                     (Using S → xB)

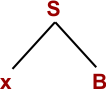
Step 02: W=  xxBB                    (Using B → xBB)

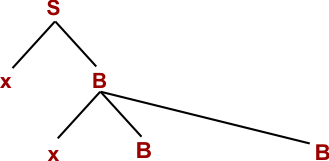
Step 03: W=  xxBxBB                 (Using B → xBB)

Step 04: W=  xxBxByS               (Using B → yS)

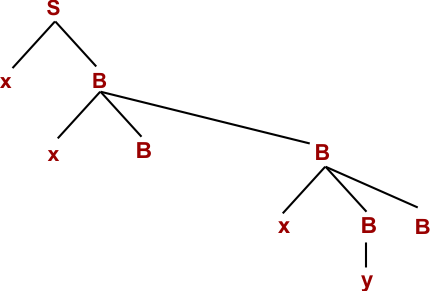
Step 05: W=  xxBxByyA             (Using S → yA)

Step 06: W= xxBxByyx              (Using A → x)

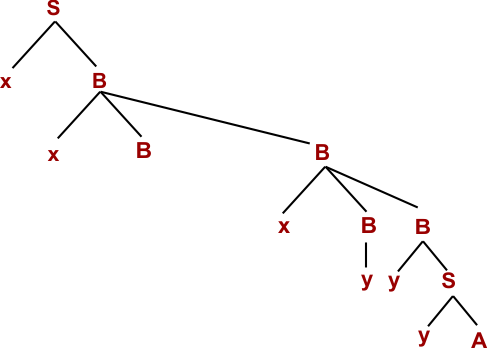
Step 07: W= xxBxyyyx              (Using B → y)

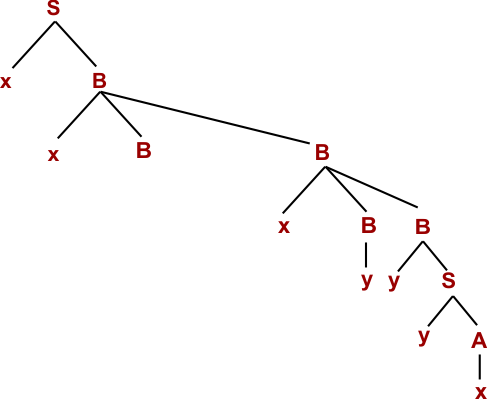
Step 08: W=  xxxBBxyyyx          (Using B → xBB)

Step 09: W=  xxxByxyyyx          (Using B → y)

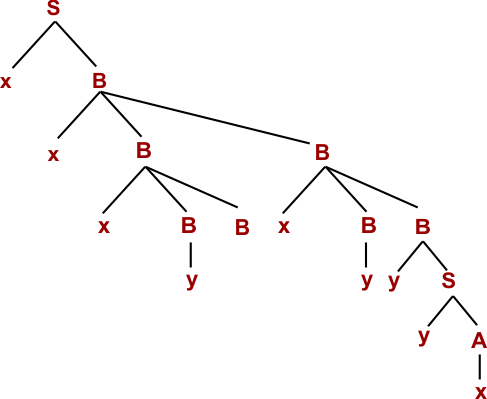
Step 10: W= xxxyyxyyyx           (Using B → y)

Hence proved the given String (W=xxxyyxyyyx) is derived through Rightmost derivation. So, given string belongs to Given Grammar (G).