Difference Between DFA and NFA

There is not much difference between DFA and NFA because they both accept regular languages. The basic difference between the DFA and NFA is that their transition function are different. 

• In DFA, the transition function (δ) takes two arguments (state, symbol) as input and returns a single state as output.
• In NFA, the transition function (δ) takes two arguments (state, symbol) as input and can return multiple states.

The following are state diagrams for both DFA and NFA to explain the very basic difference.

Here is the NFA to DFA conversion with their transition Tables

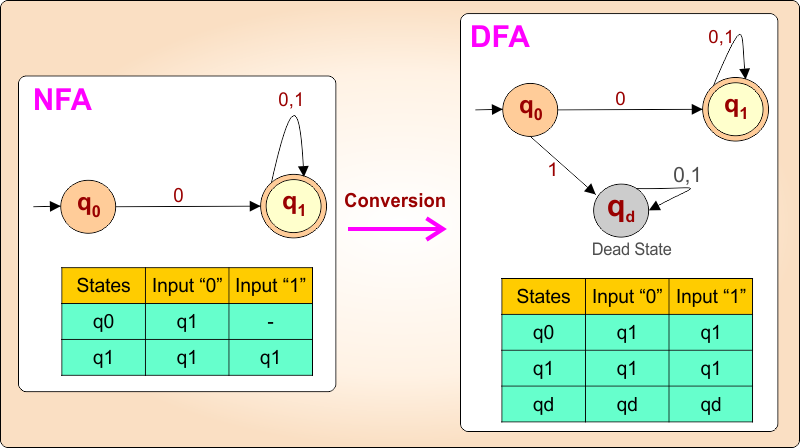
Key Difference Between DFA and NFA

Let’s explain all the Key differences in detail for DFA and NFA

1. Transition Function

Both NFA and DFA can be defined using 5 tuples (Q,Σ,δ,q0​,F). The only difference in the 5 tuples is the transition function (“δ“). Let’s explain

• DFA Transition Function (δ) : Q x Σ⇒ Q
• NFA Transition Function (δ) : Q x (Σ U ε) ⇒ 2^Q

Let’s explain three major points of difference between DFA and NFA

DFA vs NFA Transition Function: Point 01

• DFA: One input symbol can go to exactly one next state

• NFA: One input symbol can go to a single, multiple, or no states.

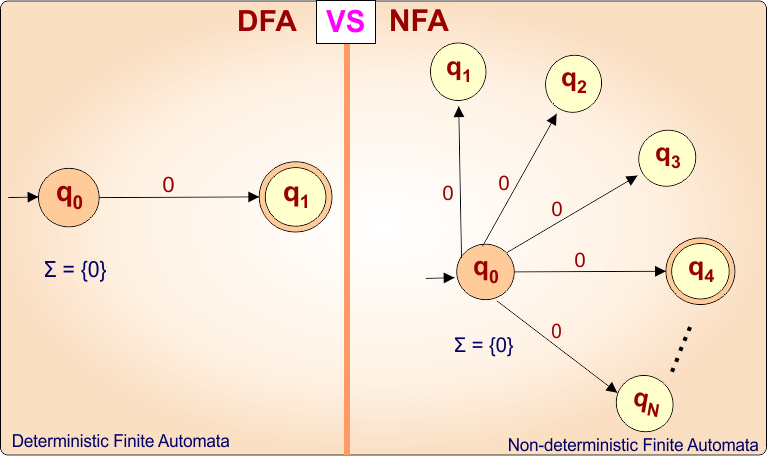
In the above state diagram for input symbols Σ = {a,b,c,d,….N}

• DFA transition function is given below.
  • δ(q0, 0) = {q1}
• NFA transition function is given below.
  •  δ(q0, 0) = {q1, q2, q3, q4,…..qN}

DFA vs NFA Transition Function: Point 02

• DFA: All input symbols (Σ) must be handled from every state.

• NFA: Not all input symbols need to be handled at every state

In the above state diagram for input symbols Σ = {a,b,c,d,….N}

• DFA transition function is given below.
  •  δ(q0, a) = {q1}
  •  δ(q0, b) = {q2}
  •  δ(q0, c) = {q3}
  • ……………………
  •  δ(q0, N) = {qN}
• NFA transition function is given below.
  •  δ(q0, a) = {q1}

DFA vs NFA Transition Function: Point 03

• DFA: No ε (epsilon) transitions

• NFA: Allows ε (epsilon) transitions (move without consuming input)

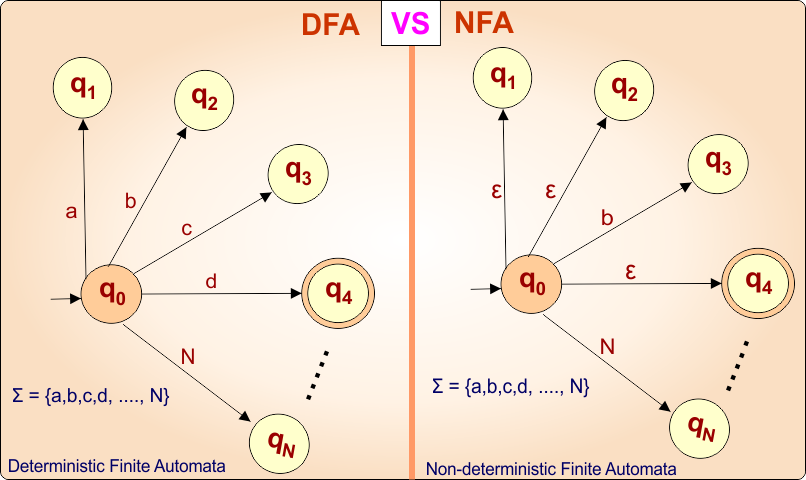
In the above state diagram for input symbols Σ = {a,b,c,d,….N}

• DFA transition function is given below.
  •  δ(q0, a) = {q1}
  •  δ(q0, b) = {q2}
  •  δ(q0, c) = {q3}
  • ……………………
  •  δ(q0, N) = {qN}
• NFA transition function is given below.
  •  δ(q0, ε) = {q1}
  •  δ(q0, ε) = {q2}
  •  δ(q0, b) = {q3}
  • ……………………
  •  δ(q0, N) = {qN}

2. Trap State / Dead State

A dead state is also called a trap state. Once the transition enters a dead state, there is no way for it to go out anywhere for further progress.  Dead/trap states are commonly used in DFAs to handle and trap invalid inputs, effectively rejecting them.

• DFAs: Dead states is more common concept in DFAs
• NFA: It is less common in NFA, it can also be identified in NFAs

Example: Draw a machine for NFA and DFA for the regular expression R = a(a+b)*

Explanation: q2 is dead state in DFA diagram because once the transition enters into the q2, it will halt there because there is no chacnce to reach at final state.

Why Dead state is more Common in DFA? Answer: A dead state is more common in a DFA because a DFA must define one transition for every input from every state, even if the input is not accepted.  In NFA, missing transitions are allowed, so dead states are often unnecessary.

3. Digital Computer Usage

NFAs can have multiple next states for a single input symbol. This introduces non-determinism, which is not desirable for digital computers.

• DFA is used in compilers, digital circuits, and real-time systems due to its deterministic and efficient behavior.
• NFA is mainly used in theory, regex pattern design, and is easier to construct but not directly implementable.

4. Every DFA is NFA But Not Vice Versa

Every DFA is an NFA that’s why we can convert every DFA to its equivalent NFA but not vice versa.

Following are two equivalent DFA and NFA which accept all strings starting with “ab”.

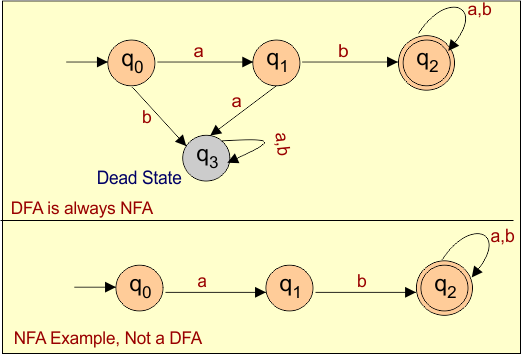
DFA diagram meets all the rules of NFA diagram, but NFA diagram does not satisfy all the rules for DFA construction.

• As in the above NFA diagram at state q0, only the transition for input “a” is made. There is no transitions is made for input “b”, so this NFA is not a DFA.

5. NFA and DFA Construction 

• DFA must define a transition for every input symbol from every state

  • This sometimes requires adding dead/trap states just to handle invalid inputs.
  • This increases the number of states and can lead to higher space usage.
  • DFA is not easy to construct because it needs one fixed path for each input from every state.

• NFAs are more flexible:

  • Transitions can be missing for some inputs.
  • Dead states are not necessary unless explicitly modeled.
  • Multiple or ε-transitions make NFAs easy to construct in many cases.

Example: Here is an example of an equivalent DFA and NFA in functionality

In the two equivalent examples of NFA and DFA, the DFA shows greater space consumption compared to the NFA.

6. NFA to DFA Conversion 

 Every NFA can be converted to its equivalent DFA. Every DFA is an NFA, but not vice versa.  But there is an equivalent DFA for every NFA.The Subset Construction Algorithm (also called Powerset Construction) is the standard method used to convert an NFA into an equivalent DFA.

i). In the NFA to DFA conversion, we create new DFA states by grouping NFA states into subsets.

• Each subset of NFA states becomes a single state in the DFA. For example If an NFA has states {q0, q1, q2}, then the DFA might have states like: {q0}, {q1}, {q0, q1}, {q0, q2}, {q1, q2}, {q0, q1, q2}, etc.

ii). While converting NFA to DFA, if the NFA maximum states are “n” states, then the resulting DFA can maximum of states are 2^n.

iii). After conversion, the resulting DFA may have redundant or unreachable states. DFA minimization algorithms can be applied to reduce the number of states in the DFA.

vi). The DFA constructed from an NFA recognizes the same language as the original NFA.

7. DFA to NFA Conversion

Every DFA is already an NFA, so no need to convert it into an NFA. If we think to minimize DFA then it is achieved by removing the possible redundant states/transitions. After minimizing DFA, result is still a valid DFA.

• Converting a DFA to an NFA does not result in an increase in the number of states
• The NFA obtained from the DFA recognizes the same language as the original DFA.

8. Time and Space complexity

While converting NFA to DFA,

• The number of states in DFA can grow exponentially up to 2^n.
• In the worst case, the time and space complexity is O(2^n). 

While converting DFA  to NFA,

• Time and space complexity is linear,
• It may remain the same or a bit reduced because the number of states are almost same.

Similarities in NFA and DFA

• Four tuples out of five are similar for both DFA and NFA except transition.
• Both DFA and NFA accept the regular languages
• NFA and DFA contains finite number of states
• NFA and DFA both can hold more than one final states
• Power of DFA and NFA is same because both types of automata are equivalent in terms of the languages they can recognize. This equivalence theorem is known as the “subset construction”. It states that every NFA has an equivalent DFA that recognizes the same language, and vice versa.
• All DFA’s are NFA’s but not vice versa.

Summary Table for DFA and NFA Difference

The top 10 differences in DFA and NFA are listed below,

Term	DFA	NFA
Stand For	DFA stands for Deterministic Finite Automata.	NFA stands for Nondeterministic Finite Automata.
For Every Input	For each sigma value (0, 1…n) there must be a provided path from each state.	For each sigma value (0, 1…n), there is no need to specify the path from each state
Digital Computers	DFA provides a path for each input, so all digital computers are deterministic.	NFA does not provide a path for each input, so NFA is not used in digital computers.
Possible Transitions	There is only one possible transition from one state on the one input symbol. It means multiple choices corresponding to an input are not available.	There is more than one possible transition from one state on the same input symbol. It means multiple choices are available corresponding to a single input.
Epsilon	DFA cannot use an Empty String. (Epsilon) transition.	NFA can use an Empty String (Epsilon) transition.
Dificulty	DFA is more difficult to construct and understand.	NFA is easier to construct and understand.
Visibility	All DFA are NFA.	All NFA are not DFA.
Space	DFA requires more space. Because it has normally more states.	NFA requires less space than DFA. Because it usually has fewer states
Dead State	Dead State are more common  in DFA	Dead State are less common in NFA
Complexity	DFA to NFA conversion, time and space complexity remain almost the same or bit reduced	NFA to DFA conversion, time and space complexity increased to exponentional.