Mealy Machine
Automata Mealy Machine is similar to the Automata Moore Machine except for the following,
- In the Automata Mealy Machine, the output symbol is represented along with the input symbol for each state. Both input and output symbols are separated by /.
- In Mealy Machine, the length of the input is always equal to the output. Because In the Mealy Machine, the first output comes by consuming the first input symbol.
- Before reaching the next state, output is received immediately as the input is consumed.
Example of Mealy Machine
An example of the Mealy Machine is given below.
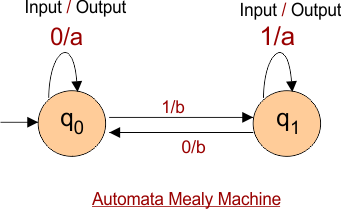
Tuples of Mealy Machine
Mealy Machine can be described by 6 tuples (Q, q0, ∑, O, δ, λ’). Let me explain the above Mealy Machine where
- q0 and q1 are states (Q).
- q0 is the initial state.
- Input alphabets (∑) are “0” and “1”.
- Output alphabets (O) are “a” and “b”.
- Transition function (Q × ∑ →Q) and output function (Q × ∑ →O) are explained in the following table
Transition Table in Mealy Machine
In Automata Mealy Machine, When the input is given, the Mealy Machine first gives an output and then goes to the next state.
In the above given Mealy Machine, the transition table is given below
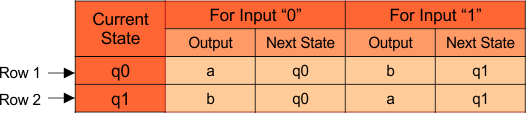
In Row 1
- When the given input is “0” at the initial state (q0), then the output will be “a,” and the Next state is also “a”.
- Similarly, When the given input is “1” at the initial state (q0), then the output will be “b” and the Next state will be “q1”.
In Row 2
- When the given input is “0” at the initial state (q1), then the output will be “b”, and the Next state is also “b.”
- Similarly, When the given input is “1” at the initial state (q1), then the output will be “a” and the Next state will also be “q1”.
Note: The output length will always equal the input’s length.
In the upcoming lecture, we will see the example of Automata Mealy Machines.













