Turing Machine For a^Nb^Nc^N
Design a Turing Machine that recognizes the language L = a^Nb^Nc^N where N>0. Given language (L = aNbNcN) will generate an equal number of a’s, b’s, and c’s. So, consider an input tap that holds L=aabbcc as given below,
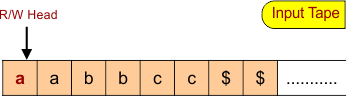
R/W Head Movement For Language a^Nb^Nc^N (aNbNcN)
Following is the R/W head movement for language a^bb^nc^n.
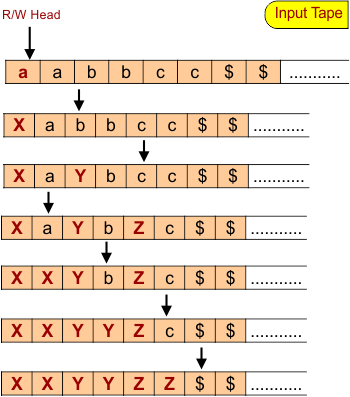
Algorithm For Language a^Nb^Nc^N (aNbNcN)
Following is the algorithm for the language a^bb^nc^n in the Turing Machine.
- Step 01: Change “a” to X, after reading “a”.
- Step 02: Move Right to the First “b”. If you find “b”, change “b” to “Y”; otherwise, reject the language.
- Step 03: Move Right to the First “c.” If “c” is found, then Change “c” to “Z”; otherwise, reject the language.
- Step 04: Move Left to Leftmost “a”
- Step 05: Repeat Steps 01 to 04 until no more “a,” b,” and “c” remain in the input tape.
Let’s construct a Turing Machine for the Language L= aabbcc.
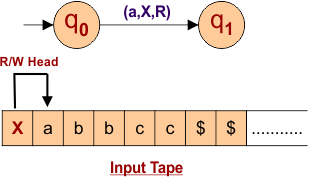
According to Step 01, Change “a” to “X”
- State change from q0 to q1
- Read/Write Head moves toward right.
The following diagram shows the input tape and Turing machine behavior.
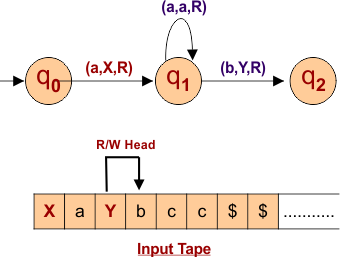
According to Step 02, change the first right b to Y.
- State change from q1 to q2
- Read/Write Head moves toward the right side
The following diagram shows the input tape and Turing machine behavior.
According to Step 03, change the first right “c” to “Z”
- State change from q2 to q3
- Read/Write Head moves toward Left.
The following diagram shows the input tape and Turing machine behavior.
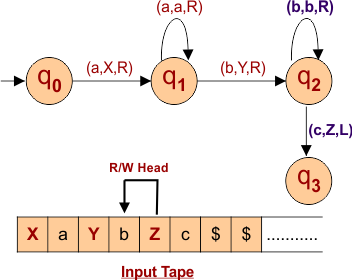
| Now repeat steps 01 to 04 to replace all “a”, “b”, and “c” with “X”, “Y”, and “Z” respectively. |
According to Step 04, Move Left to Leftmost “a”
The following diagram shows the input tape and Turing machine behavior.
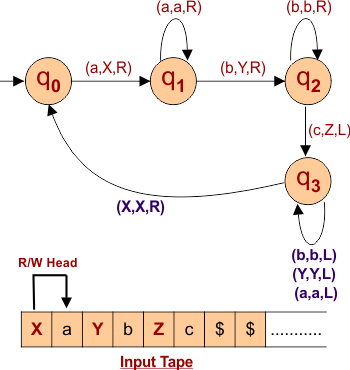
Step 05: Repetition from Step 01 to Step 04 starts
According to Step 01, replace the leftmost “a” with “X”.
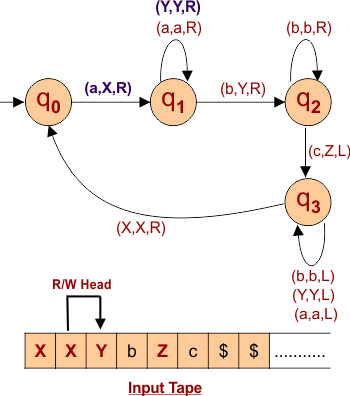
Again, According to Step 02, replace the first right “b” with “Y”.
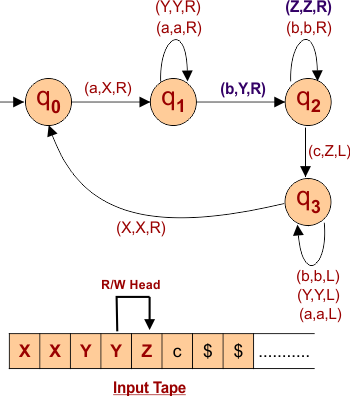
According to Step 03, change the first right “c” to “Z”. The following diagram shows the input tape and Turing machine behavior.
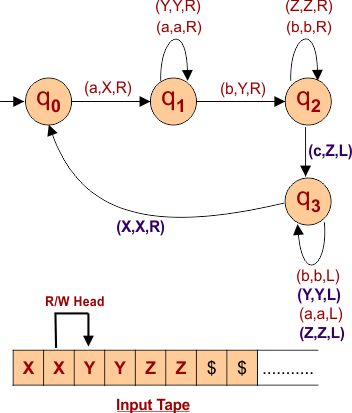
| At this point, all “a”, “b”, and “c” are replaced with “X”, “Y”, and “Z” respectively. |
The Read/Write Head points X at q0 and moves toward the right. So, to reach the special symbol “$,” consume all “X”, “Y”, and “Z”. As below.

Completion of step 05 for L = a^Nb^Nc^N
Finally, using the special symbol “$”, the R/W head moves toward the last symbol of the given language as given below, and the language is accepted.
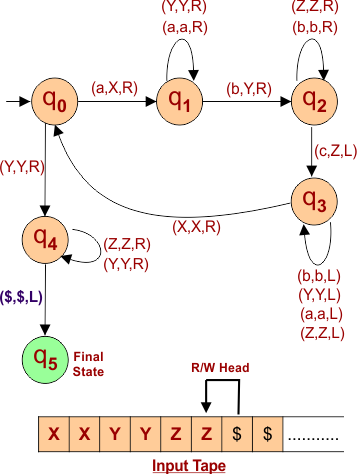
Note: After reaching the final state, the R/W head will stop moving, and we can represent it with the “N” symbol. The final transition may look like the following:
δ($,$,N)













