NFA Examples

This lecture will cover various scenarios of different categories to explain all examples of NFA. Below is a list of different categories of NFA examples.

• Followed by
• Drawing NFA from a given language
• Must contain
• and many more

We covered NFA in the last lecture. Let’s examine some examples of non-deterministic finite automata (NFA).

Category 1: Accept all strings

The first category will explain an NFA that accepts all strings over the alphabet symbols, which includes every possible combination of these symbols, including the empty string ε.

NFA Example: 1.1

Design an NFA over the alphabet Σ = {a, b} that accepts any string formed using the symbols “a” or “b”.

Solution

The language generated by this example will include the following strings

L = {ε, a, b, ab, ba, aba, aab, baa, ………….}

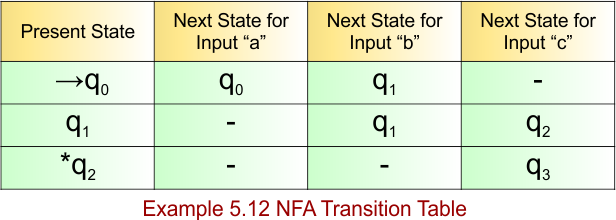
The following NFA automaton machine accepts all strings formed using the symbols a or b.

The explanation of the above NFA is given below

• States = {q0}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = q0

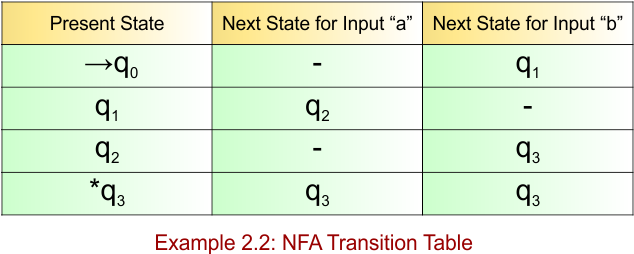
Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

NFA Example: 1.2

Design an NFA over the alphabet Σ = {a, b,c,d} that accepts any string formed using the symbols “a”, “b”, “c”,  or “d”.

Solution

The language generated by this example will include the following strings

L = {ε, a, b, c, d, ab, ba, ac, ca, ad, da, abc, abcd, ………….}

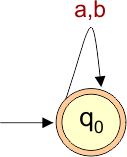
The following NFA automaton machine accepts all strings formed using the symbols “a”, “b”, “c”,  or “d”.

The explanation of the above NFA is given below

• States = {q0}
• Input Alphabet = {a, b,c,d}
• Initial State = q0
• Final State = q0

Transition Function (δ) for all input alphabets (“a,b,c,d”) is defined in the following NFA Transition Table 

 

Category 2: Start with

The second category will explain an NFA that accepts all strings that start with some fixed alphabet symbols

NFA Example: 2.1

Design an NFA over the alphabet Σ = {a, b} that accepts only the strings that start with “b”

Solution

The language generated by this example will include all strings that start with “bab”

L = {b, ba, bb, bab, baa……..}

The following NFA machine accepts all strings that start with “b”

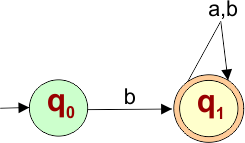
The explanation of the above NFA is given below

• States = {q0, q1}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = q1

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

  

NFA Example: 2.2

Design an NFA over the alphabet Σ = {a, b} that accepts only the strings that start with “bab”

Solution

The language generated by this example will include all strings that start with “bab”

L = {bab, baba, babb, babab, babba……..}

The following NFA automaton machine accepts all strings that start with “bab”

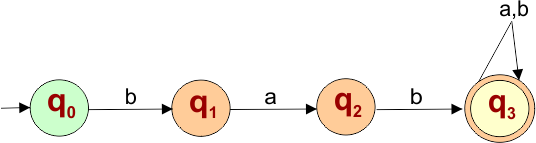
The explanation of the above NFA is given below

• States = {q0, q1, q2, q3}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = q3

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

 

NFA Example: 2.3

Design an NFA over the alphabet Σ = {a, b} that accepts only the strings that start with “aa” or “bb”

Solution

The language generated by this example will include all strings that start with “aa” or “bb”

L = { aa, bb, aaa, bbb, aaab, aaba,……..}

The following NFA automaton machine accepts all strings that start with “bab”

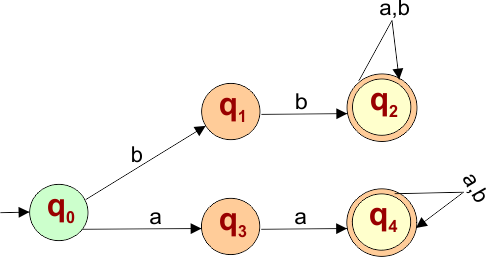
The explanation of the above NFA is given below

• States = {q0, q1, q2, q3, q4}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = q2, q4

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

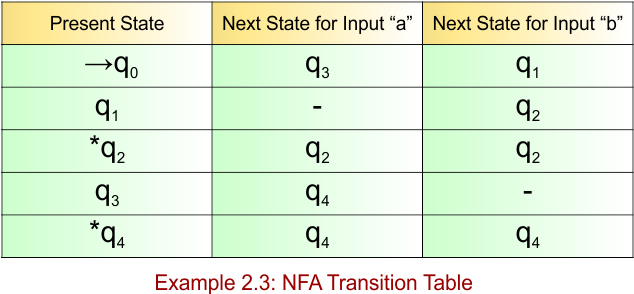
NFA Example: 2.4

Design an NFA over the alphabet Σ = {a, b} that accepts only the strings that start with “bbb” or “baab”

Solution

The language generated by this example will include all strings that start with “bbb” or “baab”

L = {bbb, baab, bbba, baaba, bbbab, bbbba, baabab, baabba, ……..}

The following NFA automaton machine accepts all strings that start with “bbb” or “baab”

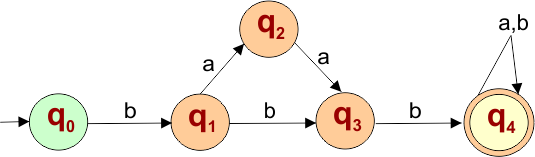
The explanation of the above NFA is given below

• States = {q0, q1, q2, q3, q4}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = q4

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

 

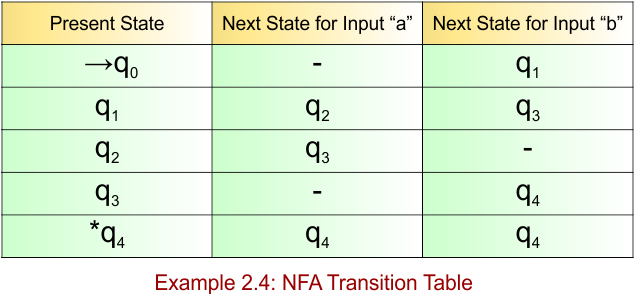
Category 3: End with

The third category will explain an NFA that accepts all strings that end with some fixed alphabet symbols

NFA Example: 3.1

Please design an NFA with input alphabet ∑ = {a, b} that accepts all the strings that end with “bab”.

Solution

The language generated by this example will include all strings that end with “bab”.

L = { bab, abab, bbab, abbab, babab……..}

The following NFA automaton machine accepts all strings that end with “bab”

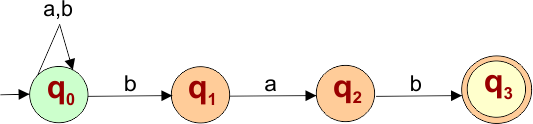
The explanation of the above NFA is given below

• States = {q0, q1, q2, q3}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = q3

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

    

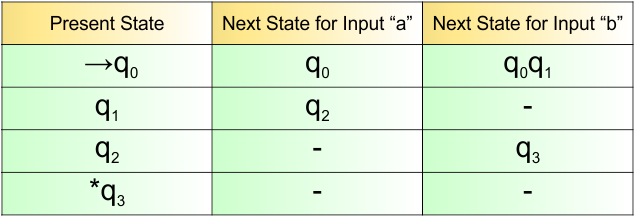
NFA Example: 3.2

Design an NFA with ∑ = {0, 1} for all binary strings where the second last bit is “1”.

Solution

The language generated by this example will include all strings in which the second-last bit is “1”.

L = { 10, 010, 000010, 11, 101011……..}

The following NFA machine accepts all strings where the second-to-last bit is “1”.

The explanation of the above NFA is given below

• States = {q0, q1, q2}
• Input Alphabet = {0, 1}
• Initial State = q0
• Final State = q2

Transition Function (δ) for all input alphabets (“0,1”) is defined in the following NFA Transition Table 

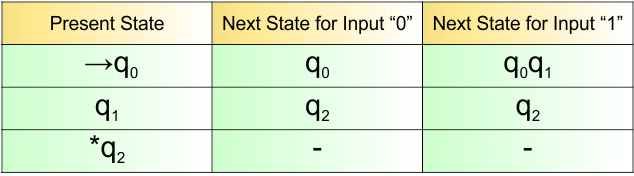
NFA Example: 3.3

Draw an NFA with ∑ = {0, 1} such that the third symbol from the right is “1”.

Solution

The language generated by this example will include all strings where the third symbol from the right is “1”.

L = {100, 111, 101, 110, 0100, 1100, 00100, 100101……..}

Required NFA is given below

The explanation of the above NFA is given below

• States = {q0, q1, q2, q3}
• Input Alphabet = {0, 1}
• Initial State = q0
• Final State = q3

Transition Function (δ) for all input alphabets (“0,1”) is defined in the following NFA Transition Table 

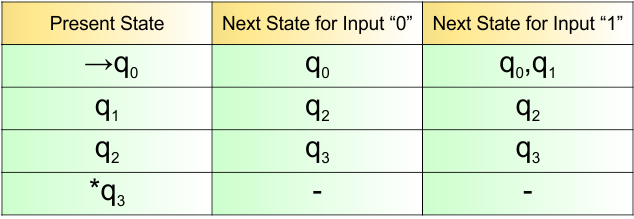
NFA Example: 3.4

Please design an NFA with input alphabet ∑ = {0, 1} that accepts all the strings that end with “01”.

Solution

The language generated by this example will include all strings that end with “01”.

L = {01, 0101, 0000101, 101, 101001……..}

The following NFA machine accepts all strings that end with “01”.

 

The explanation of the above NFA is given below

• States = {q0, q1, q2}
• Input Alphabet = {0, 1}
• Initial State = q0
• Final State = q2

Transition Function (δ) for all input alphabets (“0,1”) is defined in the following NFA Transition Table 

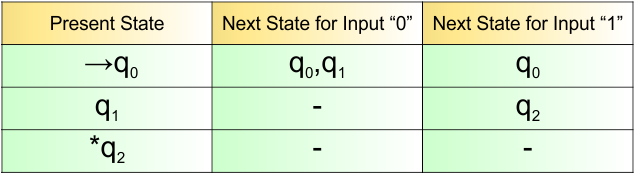
NFA Example: 3.5

Please design an NFA with input alphabet ∑ = {a, b} that accepts all the strings that end with “aa” or “bb”.

Solution

The language generated by this example will include all strings that end with “aa” or “bb”

L = { aa, bb, aaa, abb, aaaa, aabb, …………… }

The following NFA machine accepts all strings formed by zero or more repetitions of “aa” or “aab”, ending with “b”

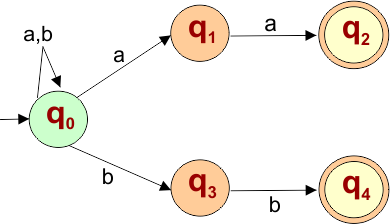
The explanation of the above NFA is given below

• States = {q0, q1, q2, q3, q4}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = {q2, q4}

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

 

NFA Example: 3.6

Please design an NFA with input alphabet ∑ = {a, b} that accepts all the strings that end with “bbb” or “bab”.

Solution

The language generated by this example will include all strings that end with “aa” or “bb”.

L = { bbb, bab, abbb, abab, bbbb, bbab, abbbb …………… }

The following NFA machine accepts all strings formed by zero or more repetitions of “aa” or “aab”, ending with “b”.

 

The explanation of the above NFA is given below

• States = {q0, q1, q2, q3, q4, q5}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = {q3, q5}

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

Category 4: Start and End with 

This category will explain an NFA that accepts all strings that start and end with some fixed alphabet symbols.

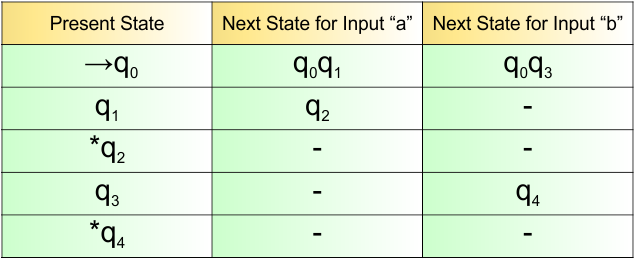
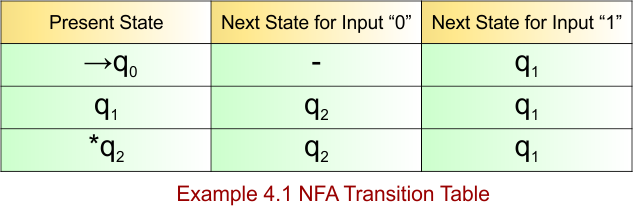
NFA Example: 4.1

Construct an NFA with ∑ = {0, 1} that accepts all strings that begin with 1 and end with 0.

Solution

The language generated by this example will include all strings that start with 1 and end with 0.

L = {10, 110, 100, 1100, 1110, 1000 ………}

Required NFA is given below

The explanation of the above NFA is given below

• States = {q0, q1, q2}
• Input Alphabet = {0,1}
• Initial State = q0
• Final State = {q2}

Transition Function (δ) for all input alphabets (“0,1”) is defined in the following NFA Transition Table 

  

NFA Example: 4.2

Please design an NFA with input alphabet ∑ = {a, b} that accepts all the strings that start with zero or more repetitions of aa and end with b.

Solution

The language generated by this example will include all strings that start with zero or more repetitions of “aa”, ending with “b”.

L = { b, aab, aaaab, aaaaaab, aaaaaaab,……….. }

The following NFA automaton machine accepts all strings that start with zero or more repetitions of “aa”, ending with “b”.

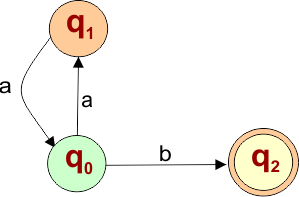
The explanation of the above NFA is given below

• States = {q0, q1, q2}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = {q2}

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

NFA Example: 4.3

Please design an NFA with input alphabet ∑ = {a, b} that accepts all the strings that start with zero or more repetitions of “aab” and end with “b”.

Solution

The language generated by this example will include all strings that start with zero or more repetitions of “aab”, ending with “b”.

L = { b, aabb, aabaabb, aabaabaabb, aabaabaaabb }

The following NFA machine accepts all strings that start with zero or more repetitions of “aab”, ending with “b”.

The explanation of the above NFA is given below

• States = {q0, q1, q2, q3}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = {q3}

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

 

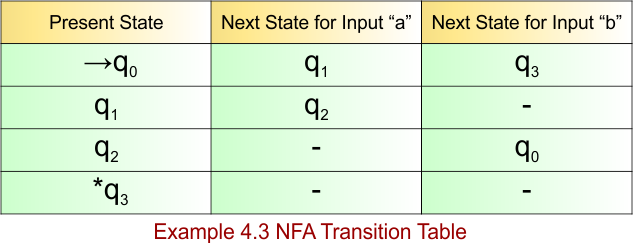
NFA Example: 4.4

Please design an NFA with input alphabet ∑ = {a, b} that accepts all the  strings that start with zero or more repetitions of “aa” or “aab”, and end with “b”.

Solution

The language generated by this example will include all strings that start with zero or more repetitions of “aa” or “aab”, and end with “b”.

L = { b, aab, aabb, aaaab, aabaabb, aabaabb, …………… }

The following NFA automaton machine accepts all strings that start with zero or more repetitions of “aa” or “aab”, and end with “b”.

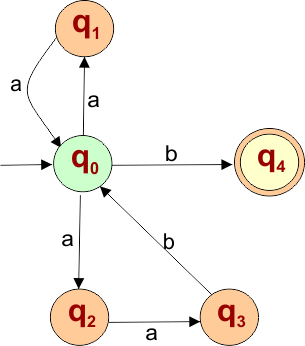
The explanation of the above NFA is given below

• States = {q0, q1, q2, q3, q4}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = {q4}

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

 

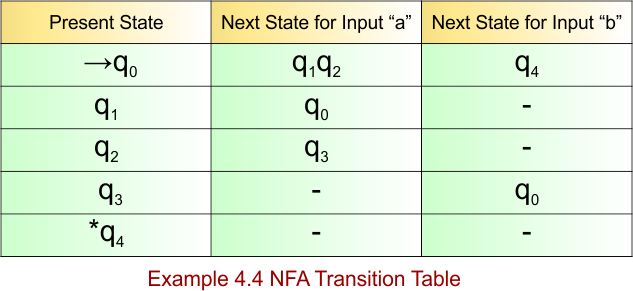
Category 05: Must Contain

This category will explain an NFA that accepts all strings that must contain a particular string as a substring.

NFA Example: 5.1

Construct an NFA with ∑ = {a, b} in which each string must contain zero or more repetitions of  “ab’ or “aab”.

Solution

The language generated by this example will include all strings that contain zero or more repetitions of  “ab’ or “aab”.

L = { ε, ab, aab, abaab, aabab, abaabaabab, …………… }

The following NFA machine accepts all strings that contain zero or more repetitions of  “ab” or “aab”.

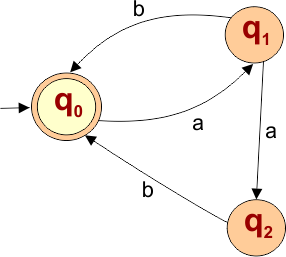
The explanation of the above NFA is given below

• States = {q0, q1, q2}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = q0

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

          

NFA Example: 5.2

Construct an NFA with ∑ = {a, b} in which each string must contain “ba” or “bb” as a substring

Solution

The language generated by this example will include all strings that contain “ba” or “bb” as a substring.

L = { bb, ba, abb, aba, bbb, bba, abbb, abba, abbbab, aaabbbbbbaaaa,  …………… }

The following NFA automaton machine accepts all strings that contain “ba” or “bb” as a substring.

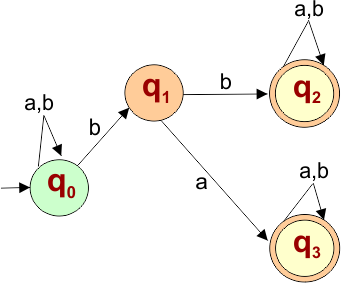
The explanation of the above NFA is given below

• States = {q0, q1, q2, q3}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = {q2, q3}

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

NFA Example: 5.3

Construct an NFA with ∑ = {a, b} in which each string must contain bbb or baab as a substring

Solution

The language generated by this example will include all strings that contain bbb or baab as a substring.

L = { bbb, baab, abbb, abaab, abbba, abaaba, bbaabb, bbbbb,  …………… }

The following NFA machine accepts all strings that contain “bbb” or “baab” as a substring. 

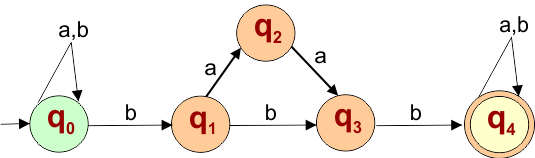
The explanation of the above NFA is given below

• States = {q0, q1, q2, q3, q4}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = {q4}

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

NFA Example: 5.4

Construct an NFA with ∑ = {a, b} in which each string must contain “bbaa” or “baba” as a substring

Solution

The language generated by this example will include all strings that contain “bbaa” or “baba” as a substring.

L = { bbaa , baba , abbaa , ababa , bbbaa, bbaba, abbaab , ababab,  …………… }

The above NFA automaton machine accepts all strings that contain “bbb” or “baab” as a substring. 

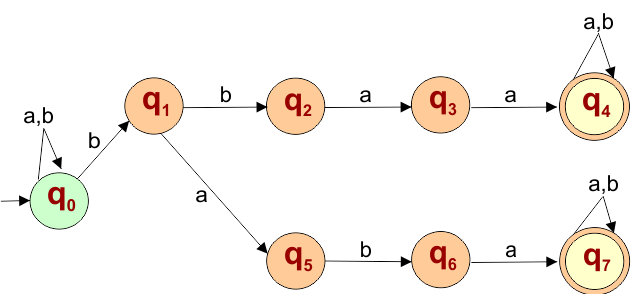
The explanation of the above NFA is given below

• States = {q0, q1, q2, q3, q4, q5, q6, q7}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = {q4, q7}

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table 

 

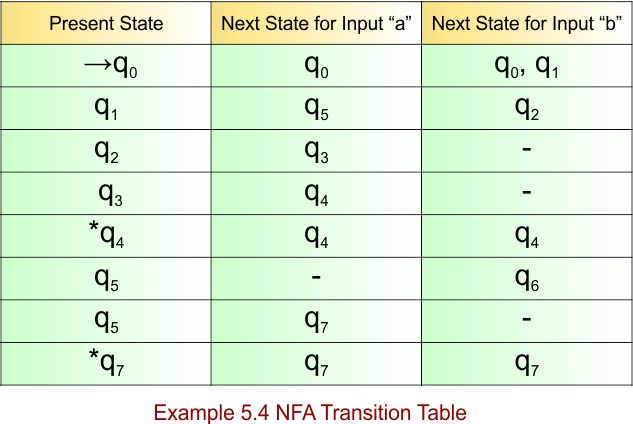
NFA Example: 5.5

Construct an NFA with ∑ = {0, 1} in which each string must contain “double ‘1’ is followed by single ‘0’.

Solution

The language generated by this example will include all strings that must contain “double ‘1’ is followed by single ‘0’.

L = {110, 0110, 1110, 10100110……..}

NFA for the above language is

The explanation of the above NFA is given below

• States = {q0, q1, q2, q3}
• Input Alphabet = {0, 1}
• Initial State = q0
• Final State = {q3}

Transition Function (δ) for all input alphabets (“0,1”) is defined in the following NFA Transition Table 

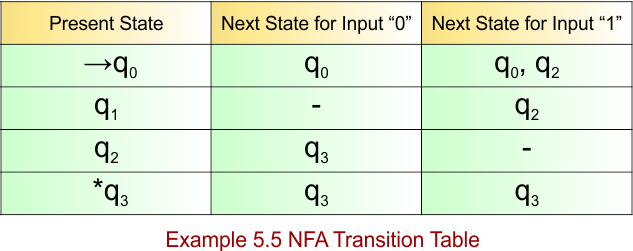
 NFA Example: 5.6

Design an NFA with ∑ = {0, 1} such that every string must contain the substring “1101”.

Solution

The language generated by this example will include all strings that must contain the substring “1101”.

L = {1101, 110101, 1101000101, 01101, 1011011……..}

NFA for the above language is

The explanation of the above NFA is given below

• States = {q0, q1, q2, q3, q4}
• Input Alphabet = {0, 1}
• Initial State = q4
• Final State = {q4}

Transition Function (δ) for all input alphabets (“0,1”) is defined in the following NFA Transition Table 

 

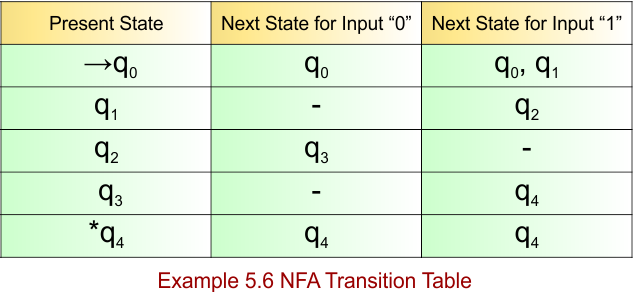
NFA Example: 5.7

Construct an NFA with ∑ = {0, 1} in which each string must contain “11” followed by “00”.

Solution

The language generated by this example will include each string that must contain “11” followed by “00”.

L = {1100, 01100, 11100, 011001, 00110001 ……..}

NFA for the above language is

The explanation of the above NFA is given below

• States = {q0, q1, q2, q3, q4}
• Input Alphabet = {0, 1}
• Initial State = q0
• Final State = q4

Transition Function (δ) for all input alphabets (“0,1”) is defined in the following NFA Transition Table 

 

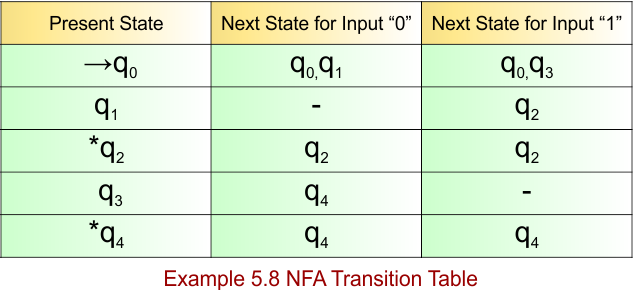
NFA Example: 5.8

Construct an NFA with ∑ = {0, 1}, where each string must contain either “01” or “10”.

Solution

The language generated by this example will include each string that must contain either “01” or “10”.

L = {01, 10, 001, 110, 1110, 0001………..}

NFA for the above language is

The explanation of the above NFA is given below

• States = {q0, q1, q2, q3, q4}
• Input Alphabet = {0, 1}
• Initial State = q0
• Final State ={q2,q4}

Transition Function (δ) for all input alphabets (“0,1”) is defined in the following NFA Transition Table 

 

•  

NFA Example: 5.9

Construct an NFA with ∑ = {0, 1} which contains the  language L = {0^m1ⁿ | m ≥0 and n≥1 }.

Solution

The language-generated strings will be like

• When m=0  and n=1, the string will be 1 because 0⁰1¹=1.
• When m=1 and n=2, then the string will be 1 because 0¹1²=011.
• When m=2 and n=3, then the string will be 1 because 0²1³=00111.
• By choosing a random value, i.e., When m=3, n=2, the string will be 1 because 0³1²=00011.And so on.

So, the string must have at least one1, but can have zero or more 0s before that.

The explanation of the above NFA is given below

• States = {q0, q1}
• Input Alphabet = {0, 1}
• Initial State = q0
• Final State = q1

Transition Function (δ) for all input alphabets (“0,1”) is defined in the following NFA Transition Table 

NFA Example: 5.10

Construct an NFA with ∑ = {0, 1} which contains the language L = {(01)ⁿ | n≥1 }.

Solution

The language-generated strings will be like as

• When n=1, the string will be 01 because (01)¹=01.
• When n=2, the string will be 0101 because (01)²=0101.
• By choosing a random value, i.e., n=5, then  (01)⁵=0101010101. And so on.

 

The explanation of the above NFA is given below

• States = {q0, q1, q2}
• Input Alphabet = {0, 1}
• Initial State = q0
• Final State = q2

Transition Function (δ) for all input alphabets (“0,1”) is defined in the following NFA Transition Table 

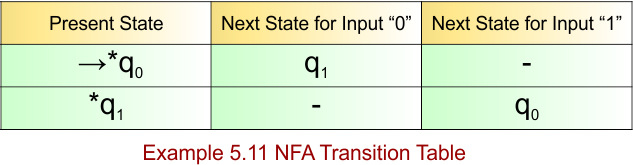
NFA Example: 5.11

Construct an NFA with ∑ = {0, 1} which contains the language L = {(01)ⁿ | n≥0 }.

Solution

The language-generated strings will be like as

• When n=0, the string will be null because (01)⁰ = null.
• If n=1, the string will be 01 because (01)¹=01.
• By choosing a random value, i.e., n=4, the result will be  (01)⁴=01010101. And so on.

The explanation of the above NFA is given below

• States = {q0, q1}
• Input Alphabet = {0, 1}
• Initial State = q0
• Final State = q1

Transition Function (δ) for all input alphabets (“0,1”) is defined in the following NFA Transition Table 

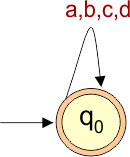
NFA Example: 5.12

Construct an NFA with ∑ = {a,b,c}  where strings contain some “a’s” followed by some “b’s” followed by some c’s.

Solution

The language-generated strings will be like as

L = {abc, aabbcc, aaabbcc, aabbbcc, aaaabbbbccc, ………… }

The explanation of the above NFA is given below

• States = {q0, q1, q2}
• Input Alphabet = {a, b}
• Initial State = q0
• Final State = q2

Transition Function (δ) for all input alphabets (“a,b”) is defined in the following NFA Transition Table