Derivation Tree in TOC

Deriving a string in the form of a tree from a CFG grammar is called a derivation tree in TOC. A Context-Free Grammar (CFG) generates strings by applying production rules. These strings can be represented in the form of a tree, which is called a derivation Tree.

Note: Derivation tree is also known as a parse Tree, or syntax tree.

A derivation tree shows how a string is formed from the start symbol of a Context-Free Grammar (CFG) by applying production rules step-by-step.

Examples of Derivations

let explain some examples of derivations in TOC

Example 01:

Suppose the following Production rules of a Grammar (G)

S → S + S | S * S  

S → x|y|z  

and Input is (x * y + Z)

Step 1: By using S → S + S

Step 2: By using S → S * S

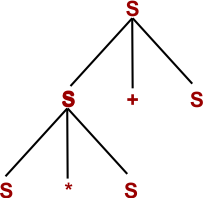
Step 3: By using S → x

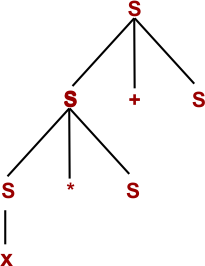
Step 4: By using S → y

 

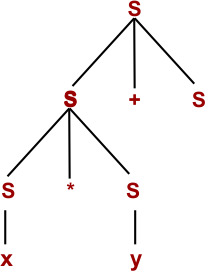
Step 5: By using S → z

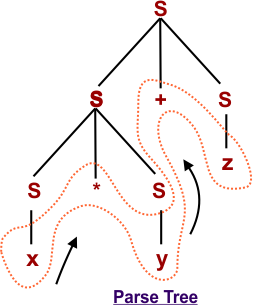
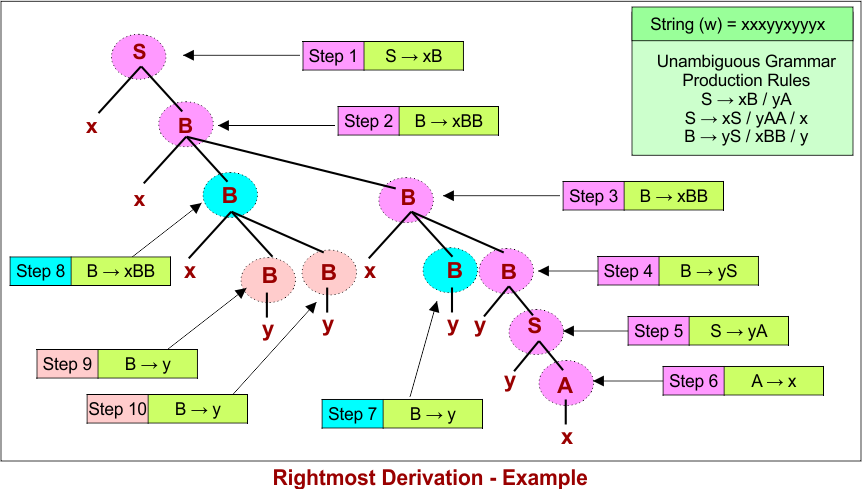
Example 02:

Grammar Production Rules are
S → xB / yA
S → xS / yAA / x
B → yS / xBB / y

Input string is “xxxyy“

How Derivation Works?

It is called a tree because:

• Start with the start symbol (a non-terminal) at the top of the tree (root).
• Apply production rules to expand non-terminals into other non-terminals or terminals, forming branches.
• Repeat expansions until all branches end in terminal symbols (no non-terminals remain).
• The leaf nodes (terminals), read from left to right, form the final generated string.

Elements in Derivation Tree

The major components of the derivation tree are given below

• Non-terminal symbols: Intermediate symbols used in derivation (e.g., S, A, B)
• Terminal symbols: Final output symbols (e.g., a, b, c)
• Production rules: Rules that guide replacement (e.g., S → aSb | ε)
• Start symbol: The symbol from where derivation begins (usually S)

Need for Derivation

A derivation tree is helpful when a string and a grammar (set of production rules) are given, and we need to check whether the string can be generated by the grammar or not. The main goals of using derivations are given below

• Shows how a string is formed step-by-step by applying grammar rules from the start symbol to terminals.
• Helps compilers understand code structure by breaking programs into meaningful parts during parsing.
• Identifies ambiguity, ambiguity means that if two different trees can be drawn for the same string, then the grammar is ambiguous.
• Checks syntax correctness by ensuring the code follows the grammar rules of the language.

Types of Derivation

There are two main types of derivation trees

1. Leftmost Derivation Tree

• In a leftmost derivation, at each step, the leftmost non-terminal in the current string is expanded first using a production rule.

• This method is useful in top-down parsing techniques, like recursive descent parsers.

Here is descriptive diagram of the leftmost derivation tree

2. Rightmost Derivation Tree

• In a rightmost derivation, at each step, the rightmost non-terminal in the current string is expanded first.

• Rightmost derivations are commonly used in bottom-up parsing algorithms, such as shift-reduce parsers.

Here is discriptive diagram of rightmost derivation tree

 Ambiguity in Derivation Trees

A grammar is called ambiguous if there exists at least one string in the language that can be generated by two or more different derivation trees (or parse trees).

Example:

Production rules: S → xB | xy , A → AB | x , B → Ayy | y

Given string (W) to derive: xy.

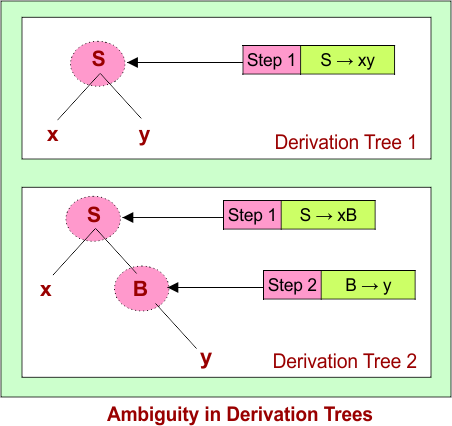
• Ambiguity means there are multiple ways to apply production rules to derive the same string, leading to different tree structures.
• Ambiguous grammars can cause confusion in parsing, as the meaning or structure of the string is not uniquely defined, which is undesirable for programming languages.

Properties Of Derivation Tree

In the derivation tree

• The root node of a parse tree represents the start symbol of the grammar.
• Each leaf node corresponds to a terminal symbol, while each interior node represent a non-terminal symbol.
• The structure of the parse tree remains unaffected by the order in which the production rules are applied during the derivations.