Epsilon NFA to DFA
In automata theory, converting an Epsilon NFA to a DFA is an essential process for achieving fast and deterministic execution. While Epsilon-NFAs and NFAs are easier to design due to their flexibility and non-determinism, most real-world systems like lexical analyzers, compilers, and tokenizers require deterministic behavior—hence, the need for DFA conversion.
- Epsilon-NFA allows epsilon (ε) transition, easy to design, but not directly usable by machines.
- DFA has only one path per input, no ε-transition, and is fast and ready for execution.
Algorithm for Epsilon NFA to DFA Conversion
A simple 3-step algorithm can be used to convert the given epsilon NFA to DFA
Step 01: Find the Epsilon closure of “q0”, which will be the First State of the DFA
Step 02: Identify the transitions for each input symbol at every state. These transitions utilize the subset construction method.
- For a particular input, apply transition (δ) to each state in the current set and take the union of all results.
- Apply ε-closure to the resulting set to get the next DFA state.
Step 2 will repeat for all new states for the DFA.
Step 03: Identify final states of the ε-NFA. In the DFA, mark any state as final if it contains at least one ε-NFA final state.
You Must Know
ε-closure: All the states that can be reached from a particular state using only ε (epsilon) transitions are called the ε-closure of that state.
For Example: If q0 →ε→ q1 →ε→ q2, then
- ε-closure(q0) = {q0, q1, q2}
- ε-closure(q1) = {q1, q2}
- ε-closure(q2) = {q2}
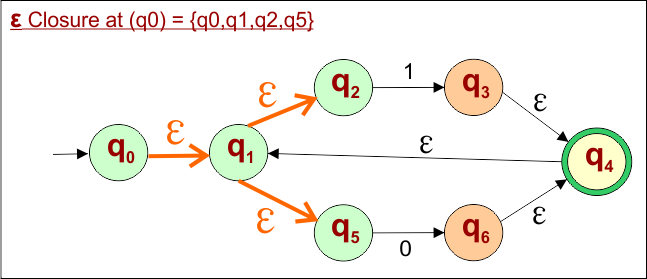
Example 01: Epsilon NFA to DFA
Here is the given NFA, which needs to be converted into a DFA
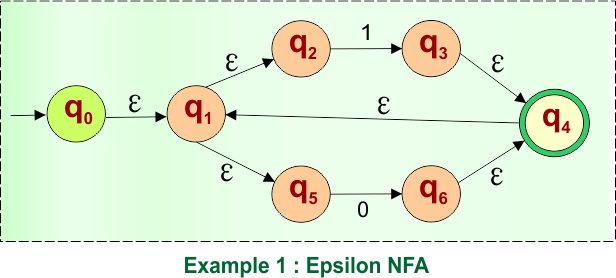
Step 01: Find the Epsilon closure of “q0”
The epsilon closure of state “q0” in the given epsilon NFA example includes states “q0,” “q1,” “q2,” and “q5,” as we can reach these states only using epsilon transitions.
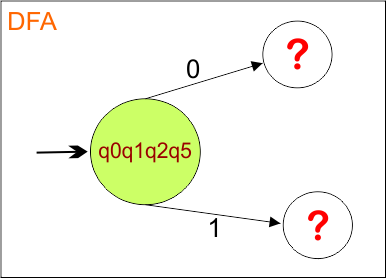
DFA First State: The result of “q0 epsilon clouser”, which is {q0,q1,q2,q5}, will be the initial state of the DFA. DFA with its initial state is given below
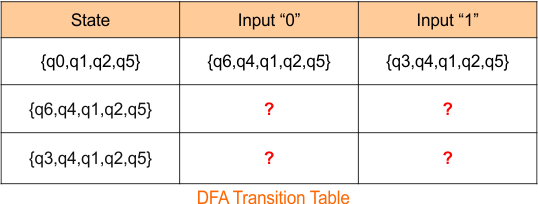
The DFA transition table with its initial state is given below
In a DFA, we must determine the transition for each input symbol at every state. Let’s start
Step 02: Identify Transitions for each input symbol at every state
According to the transition rule of Epsilon NFA to DFA conversion, let’s start finding the transitions
Step 2.1: Identify Transitions for the Initial state “{q0,q1,q2,q5}”
Transition For input “0”
- δ {(q0,q1,q2,q5), 0} = ε Closure {δ(q0,0) U δ(q1,0) U δ(q2,0) U δ(q5,0)}
- δ {(q0,q1,q2,q5), 0} = ε Closure {ϕ U ϕ U ϕ U q6}
- δ {(q0,q1,q2,q5), 0} = ε Closure { q6 }
- δ {(q0,q1,q2,q5), 0} = {q6,q4,q1,q2,q5} // Next state
Transition For input “1”
- δ {(q0,q1,q2,q5), 1} = ε Closure {δ(q0,1) U δ(q1,1) U δ(q2,1) U δ(q5,1)}
- δ {(q0,q1,q2,q5), 1} = ε Closure {ϕ U ϕ U q3 U ϕ}
- δ {(q0,q1,q2,q5), 1} = ε Closure { q3 }
- δ {(q0,q1,q2,q5), 1} = {q3,q4,q1,q2,q5} // Next state
The DFA transition table is updated as below
The DFA Diagram is updated as given below.
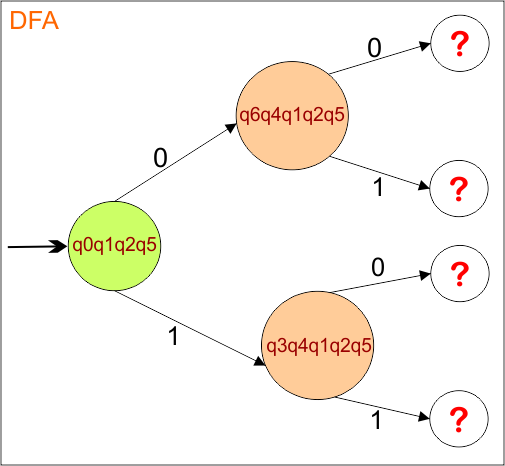
Now, we need to find a transition for state {q6,q4,q1,q2,q5} and {q3,q4,q1,q2,q5} for both input symbols “0” and “1”.
Step 2.2: Identify Transitions for the state “{q6,q4,q1,q2,q5}”
Transition For input “0”
- δ {(q6,q4,q1,q2,q5), 0} = ε Closure { δ(q6,0) U δ(q4,0) U δ(q1,0) U δ(q2,0) U δ(q5,0)}
- δ {(q6,q4,q1,q2,q5), 0} = ε Closure { ϕ U ϕ U ϕ U ϕ U q6 }
- δ {(q6,q4,q1,q2,q5), 0} = ε Closure { q6 }
- δ {(q6,q4,q1,q2,q5), 0} = {q6,q4,q1,q2,q5} // Next state
Transition For input “1”
- δ {(q6,q4,q1,q2,q5), 1} = ε Closure { δ(q6,1) U δ(q4,1) U δ(q1,1) U δ(q2,1) U δ(q5,1)}
- δ {(q6,q4,q1,q2,q5), 1} = ε Closure { ϕ U ϕ U ϕ U q3 U ϕ }
- δ {(q6,q4,q1,q2,q5), 1} = ε Closure { q3 }
- δ {(q6,q4,q1,q2,q5), 1} = {q3,q4,q1,q2,q5} // Next state
The DFA transition table is updated as below
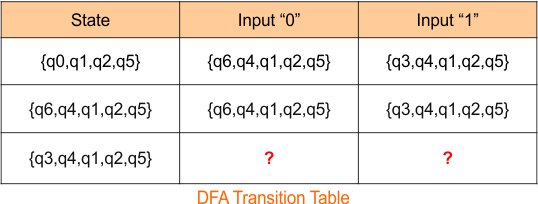
The DFA Diagram is updated as given below.
Now, we need to find a transition for state {q3,q4,q1,q2,q5} for both input symbols “0” and “1”.
Step 2.3: Identify Transitions for the state “{q3,q4,q1,q2,q5}”
Transition For input “0”
- δ {(q3,q4,q1,q2,q5), 0} = ε Closure { δ(q3,0) U δ(q4,0) U δ(q1,0) U δ(q2,0) U δ(q5,0)}
- δ {(q3,q4,q1,q2,q5), 0} = ε Closure { ϕ U ϕ U ϕ U ϕ U q6 }
- δ {(q3,q4,q1,q2,q5), 0} = ε Closure { q6 }
- δ {(q3,q4,q1,q2,q5), 0} = {q6,q4,q1,q2,q5} // Next state
Transition For input “1”
- δ {(q3,q4,q1,q2,q5), 1} = ε Closure { δ(q3,1) U δ(q4,1) U δ(q1,1) U δ(q2,1) U δ(q5,1)}
- δ {(q3,q4,q1,q2,q5), 1} = ε Closure { ϕ U ϕ U ϕ U q3 U ϕ }
- δ {(q3,q4,q1,q2,q5), 1} = ε Closure { q3 }
- δ {(q3,q4,q1,q2,q5), 1} = {q3,q4,q1,q2,q5} // Next state
The DFA transition table is updated as below
The DFA Diagram is updated as given below.
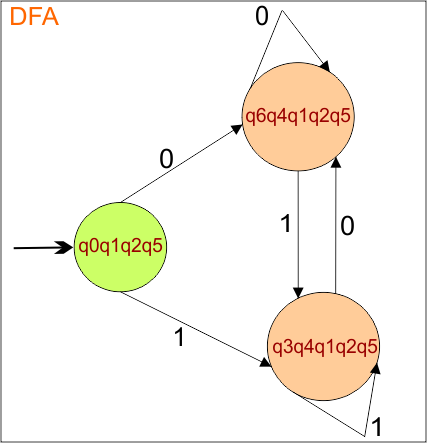
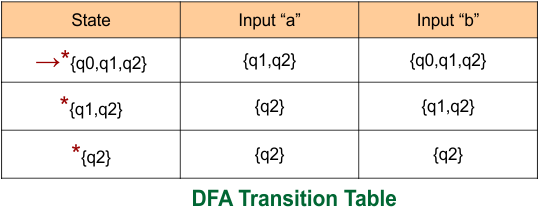
DFA condition for transitions is completed, no state remains for its transition. Now mark only the final states using a double circle symbol.
Step 03: Identify the Final States
In the given epsilon NFA, the state q4 was the final state. Therefore, all states in the DFA that include state “q4” are final. So, DFA with its Final states is given below
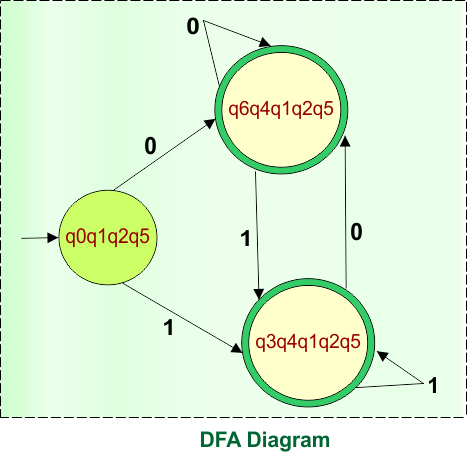
Thus, the above DFA is now complete and is equivalent to the given epsilon NFA in example 01. The transition table of this DFA is given below
Example 02: Epsilon NFA to DFA
Here is the given NFA, which needs to be converted into a DFA
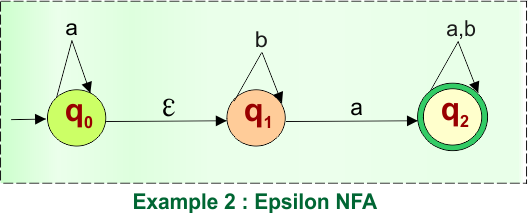
Step 01: Find the Epsilon closure of “q0”
The epsilon closure of state “q0” in the given epsilon NFA example includes states “q0” and “q1,” as we can reach these states only using epsilon transitions.
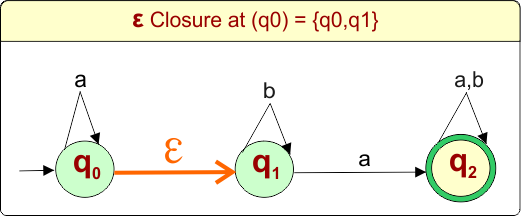
DFA First State: The result of “q0 epsilon clouser”, which is {q0,q1}, will be the initial state of the DFA. DFA with its initial state is given below
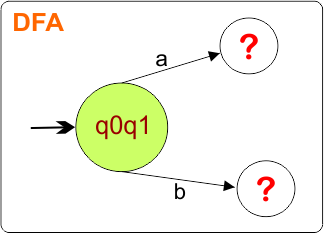
The DFA transition table with its initial state is given below
In a DFA, we must determine the transition for each input symbol at every state.
Step 02: Identify Transitions for each input symbol at every state
According to the transition rule of Epsilon NFA to DFA conversion, let’s start finding the transitions
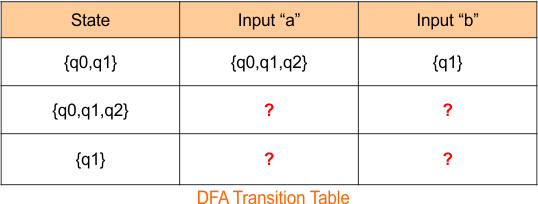
Step 2.1: Identify Transitions for the Initial state “{q0,q1}”
Transition For input “a”
- δ {(q0,q1), a} = ε Closure { δ(q0,a) U δ(q1,a)}
- δ {(q0,q1), a} = ε Closure { q0 U q2}
- δ {(q0,q1), a} = ε Closure { q0,q2 }
- δ {(q0,q1), a} = ε Closure { q0} U ε Closure { q2 }
- δ {(q0,q1), a} = { q0, q1} U { q2 }
- δ {(q0,q1), a} = { q0, q1, q2 } // Next state
Transition For input “b”
- δ {(q0,q1), b} = ε Closure { δ(q0,b) U δ(q1,b)}
- δ {(q0,q1), b} = ε Closure { ϕ U q1 }
- δ {(q0,q1), b} = ε Closure { q1 }
- δ {(q0,q1), b} = {q1} // Next state
The DFA transition table is updated as follows
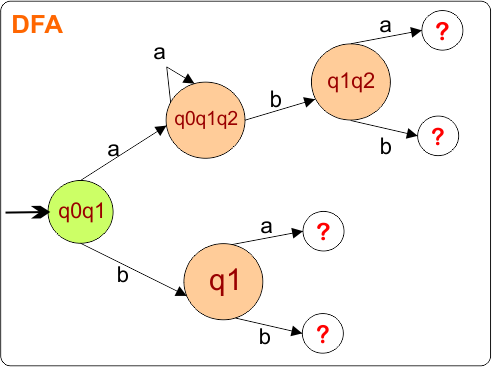
The DFA Diagram is updated as given below.
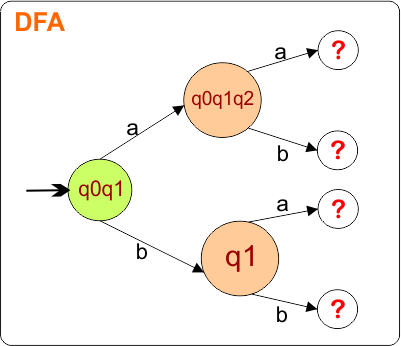
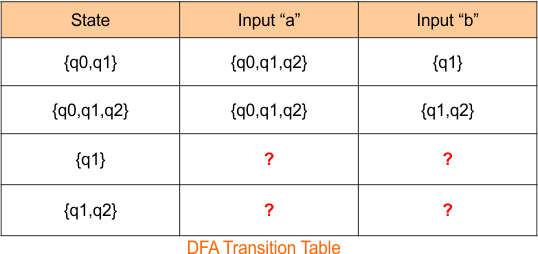
Now, we need to find a transition for state { q0, q1, q2 } and { q1 } for both input symbols “a” and “b”.
Step 2.2: Identify Transitions for the state “{ q0, q1, q2 } “
Transition For input “a ”
- δ {(q0,q1,q2), a} = ε Closure { δ(q0,a) U δ(q1,a) U δ(q2,a)}
- δ {(q0,q1,q2), a} = ε Closure { q0 U q2 U q2}
- δ {(q0,q1,q2), a} = ε Closure { q0,q2 }
- δ {(q0,q1,q2), a} = ε Closure { q0 } U ε Closure { q2 }
- δ {(q0,q1,q2), a} = { q0,q1 } U { q2}
δ {(q0,q1,q2), a} = { q0q1q2 } // Next state
Transition For input “b”
- δ {(q0,q1,q2), b} = ε Closure { δ(q0,b) U δ(q1,b) U δ(q2,b)}
- δ {(q0,q1,q2), b} = ε Closure { ϕ U q1 U q2}
- δ {(q0,q1,q2), b} = ε Closure { q1,q2}
- δ {(q0,q1,q2), b} = ε Closure { q1 } U ε Closure { q2 }
- δ {(q0,q1,q2), b} = { q0} U { q2}
- δ {(q0,q1,q2), b} = { q1,q2 } // Next state
The DFA transition table is updated as follows
The DFA Diagram is updated as given below.
No, we need to find a transition for state {q1,q2} and {q1} for both input symbols “a” and “b”.
Step 2.3: Identify Transitions for the state “q1”
Transition For input “a”
- δ {(q1), a} = ε Closure { δ(q1,a)}
- δ {(q1), a} = ε Closure {q2}
- δ {(q1), a} = {q2 } // Next state
Transition For input “b”
- δ {(q1), b} = ε Closure { δ(q1,b)}
- δ {(q1), b} = ε Closure {q1}
- δ {(q1), b} = { q1} // Next state
The DFA transition table is updated as follows
The DFA Diagram is updated as given below.
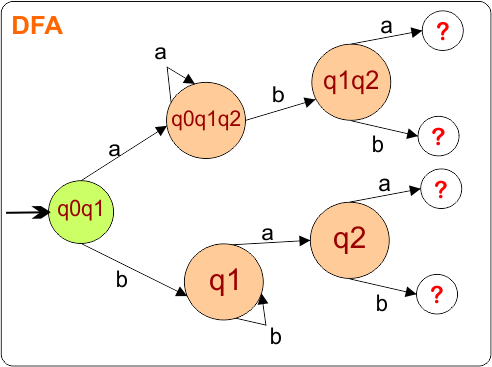
Now, we need to find a transition for state {q1,q2} and {q2} for both input symbols “a” and “b”.
Step 2.4: Identify Transitions for the state “q1q2”
Transition For input “a”
- δ {(q1,q2), a} = ε Closure {δ(q1,a) U δ(q2,a)}
- δ {(q1,q2), a} = ε Closure { q2 U q2}
- δ {(q1,q2), a} = ε Closure { q2 }
- δ {(q1,q2), a} = { q2 } // Next state
Transition For input “b”
- δ {(q1,q2), b} = ε Closure { δ(q1,b) U δ(q2,b)}
- δ {(q1,q2), b} = ε Closure { q1 U q2}
- δ {(q1,q2), b} = ε Closure { q1,q2}
- δ {(q1,q2), b} = ε Closure { q1} U ε Closure {q2}
- δ {(q1,q2), b} = { q1} U {q2}
- δ {(q1,q2), b} = { q1, q2} // Next state
The DFA transition table is updated as below
The DFA Diagram is updated as given below.
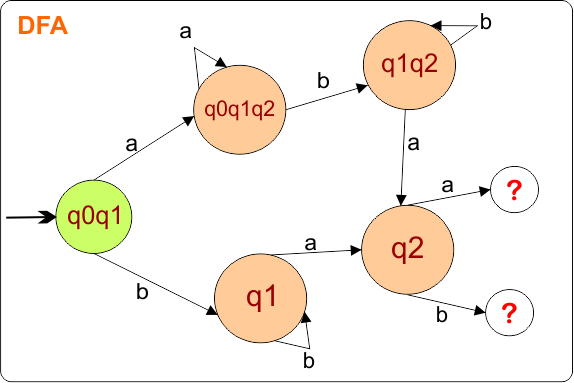
Now, we need to find a transition for state {q2} for both input symbols “a” and “b”.
Step 2.1: Identify Transitions for the state “q2”
Transition For input “a”
- δ {(q2), a} = ε Closure {δ(q2,a)}
- δ {(q2), a} = ε Closure {q2}
- δ {(q2), a} = {q2 } // Next state
Transition For input “b”
- δ {(q2), b} = ε Closure { δ(q2,b)}
- δ {(q2), b} = ε Closure {q2}
- δ {(q2), b} = { q2} // Next state
The DFA transition table is updated as follows
The DFA Diagram is updated as given below.
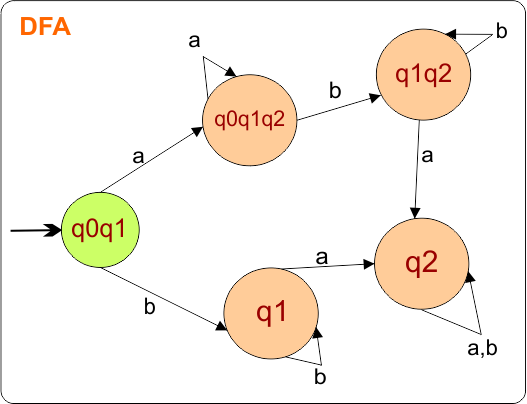
DFA condition for transitions is completed, no state remains for its transition. Now mark only the final states using a double circle identification.
Step 03: Identify the Final States
In the given epsilon NFA, the state q2 was the final state. Therefore, all states in the DFA that include state “q2” are final. So, DFA with its Final states is given below
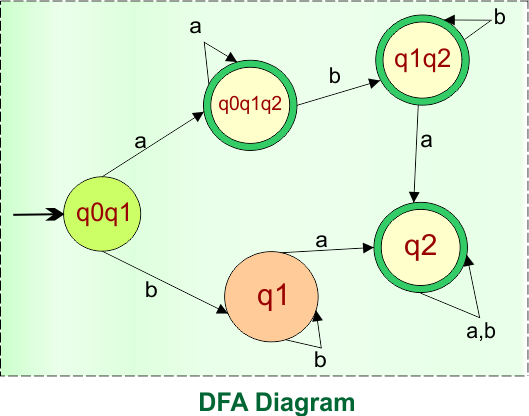
Thus, the above DFA is now complete and is equivalent to the given epsilon NFA in example 02. The transition table of this DFA is given below
Example 03: Epsilon NFA to DFA
Here is the given NFA, which needs to be converted into a DFA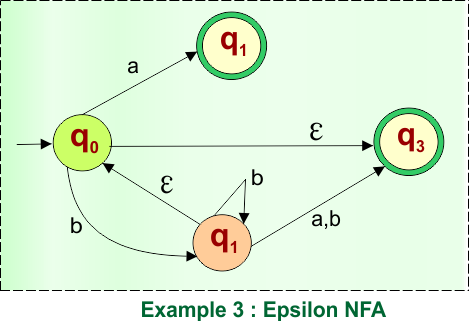 
Step 01: Find the Epsilon closure of “q0”
The epsilon closure of state “q0” in the given epsilon NFA example includes states “q0” and “q3” as we can reach these states only using epsilon transitions.
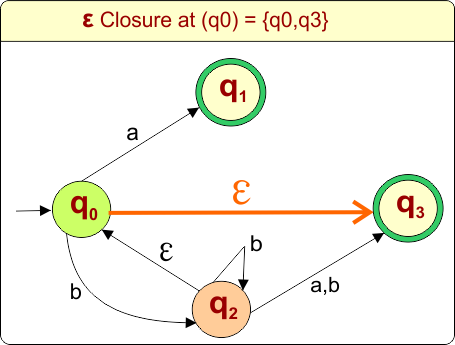
DFA First State: The result of “q0 epsilon clouser”, which is {q0,q3}, will be the initial state of the DFA. DFA with its initial state is given below
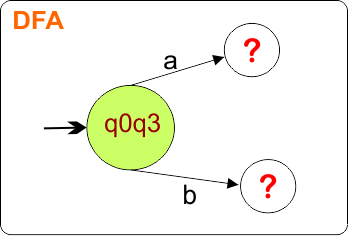
The DFA transition table with its initial state is given below
In a DFA, we must determine the transition for each input symbol at every state. Now, we need to find a transition for state {q0,q3} for both input symbols “a” and “b”.
Step 02: Identify Transitions for each input symbol at every state
According to the transition rule of Epsilon NFA to DFA conversion, let’s start finding the transitions
Step 2.1: Identify Transitions for the initial state “{q0,q3}”
Transition For input “a”
- δ {(q0,q3), a} = ε Closure { δ(q0,a) U δ(q3,a)}
- δ {(q0,q3), a} = ε Closure { q1 U ϕ}
- δ {(q0,q3), a} = ε Closure { q1}
- δ {(q0,q3), a} = { q1} // Next state
Transition For input “b”
- δ {(q0,q3), b} = ε Closure { δ(q0,b) U δ(q3,b)}
- δ {(q0,q3), b} = ε Closure { q2 U ϕ}
- δ {(q0,q3), b} = ε Closure { q2 }
- δ {(q0,q3), b} = {q2,q0,q3} // Next state
The DFA transition table is updated as below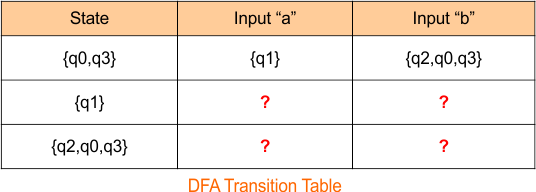
The DFA Diagram is updated as given below.
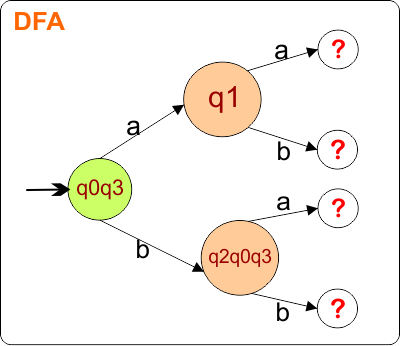
Now, we need to find a transition for state {q1} and {q2,q0,q3} for both input symbols “a” and “b”.
Step 2.2: Identify Transitions for the state “q1”
Transition For input “a”
- δ {(q1), a} = ε Closure { δ(q1,a)}
- δ {(q1), a} = ε Closure {ϕ}
- δ {(q1), a} = { ϕ } // Next state
Transition For input “b”
- δ {(q1), b} = ε Closure { δ(q1,b)}
- δ {(q1), b} = ε Closure {ϕ}
- δ {(q1), b} = { ϕ } // Next state
The DFA transition table is updated as follows
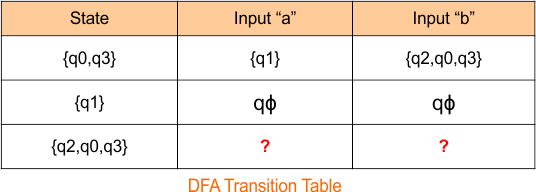
The DFA Diagram is updated as given below.
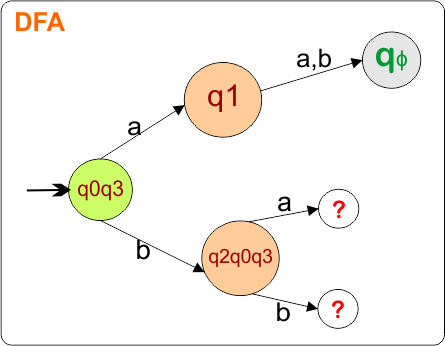
Now, we need to find a transition for state {q2,q0,q3} and {qϕ} for both input symbols “a” and “b”.
Step 2.3: Identify Transitions for the state “{q2,q0,q3}”
Transition For input “a”
- δ {(q2,q0,q3), a} = ε Closure { δ(q2,a) U δ(q0,a) U δ(q3,a)}
- δ {(q2,q0,q3), a} = ε Closure { q3 U q1 U ϕ }
- δ {(q2,q0,q3), a} = ε Closure { q3,q1 }
- δ {(q2,q0,q3), a} = ε Closure { q3 } U ε Closure { q1 }
- δ {(q2,q0,q3), a} = { q3 } U { q1}
- δ {(q2,q0,q3), a} = { q3, q1 } // Next state
Transition For input “b”
- δ {(q2,q0,q3), b} = ε Closure { δ(q2,b) U δ(q0,b) U δ(q3,b)}
- δ {(q2,q0,q3), b} = ε Closure { q2,q3 U q2 U ϕ }
- δ {(q2,q0,q3), b} = ε Closure { q2, q3}
- δ {(q2,q0,q3), b} = ε Closure { q2 } U ε Closure { q3 }
- δ {(q2,q0,q3), b} = { q2 , q0 , q3 } U { q3}
- δ {(q2,q0,q3), b} = { q2 , q0 , q3} // Next state
The DFA transition table is updated as follows
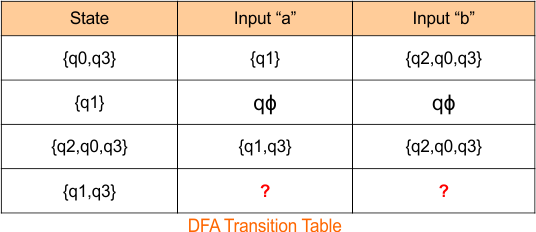
The DFA Diagram is updated as given below.
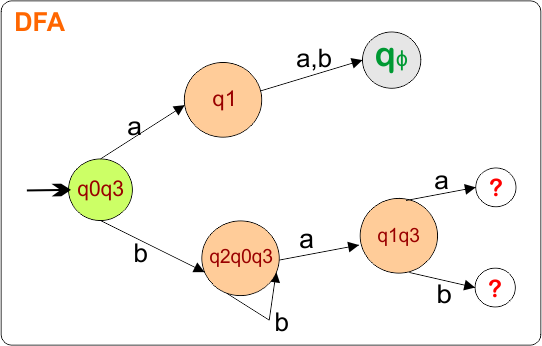
Now, we need to find a transition for state {q1q3} and { qϕ} for both input symbols “a” and “b”.
Step 2.4: Identify Transitions for the state “q1q3”
Transition For input “a”
- δ {(q1,q3), a} = ε Closure {δ(q1,a) U δ(q3,a)
- δ {(q1,q3), a} = ε Closure {ϕ U ϕ}
- δ {(q1,q3), a} = ε Closure { ϕ }
- δ {(q1,q3), a} = { ϕ } // Next state
Transition For input “b”
- δ {(q1,q3), b} = ε Closure {δ(q1,b) U δ(q3,b)}
- δ {(q1,q3), b} = ε Closure {ϕ U ϕ}
- δ {(q1,q3), b} = ε Closure { ϕ }
- δ {(q1,q3), b} = {ϕ} // Next state
The DFA transition table is updated as follows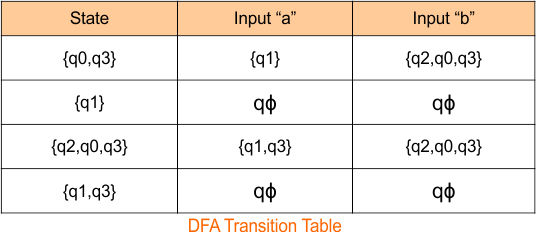
The DFA Diagram is updated as given below.
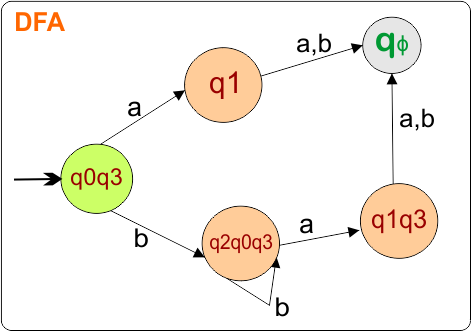
Now, we need to find a transition for state {qϕ } for both input symbols “a” and “b”.
Step 2.5: Identify Transitions for the state “qϕ “
qϕ transitions for all input symbols will always self-loop (“qϕ “). The DFA transition table is updated as follows
The DFA Diagram is updated as given below.
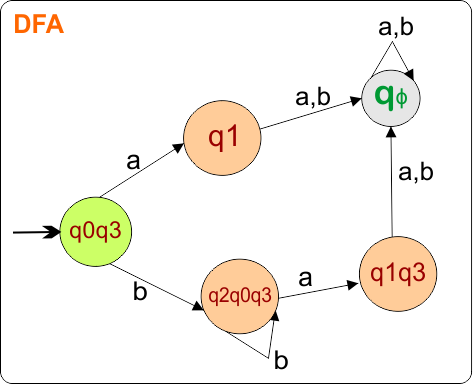
DFA condition for transitions is completed, no state remains for its transition. Now mark only the final states using a double circle symbol.
Step 03: Identify the Final States
In the given epsilon NFA, the states “q1” and “q3” were the final states. Therefore, all states in the DFA that include these states are final. So, DFA with its Final states is given below
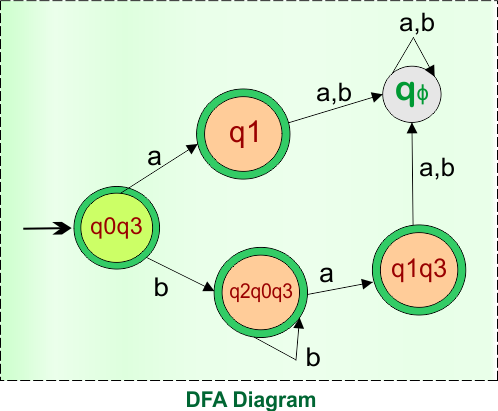
Thus, the above DFA is now complete and is equivalent to the given epsilon NFA in example 03. The transition table of this DFA is given below
Example 04: Epsilon NFA to DFA
Here is the given NFA, which needs to be converted into a DFA
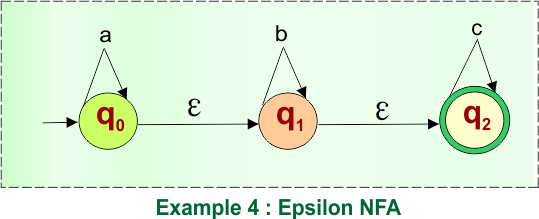
Step 01: Find the Epsilon closure of “q0”
The epsilon closure of state “q0” in the given epsilon NFA example includes states “q0”, “q1”, and “q2” as we can reach these states only using epsilon transitions.
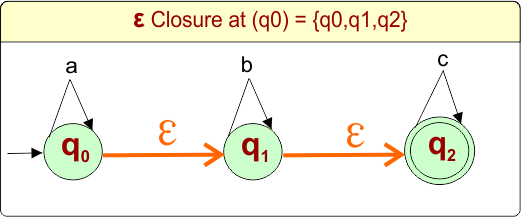
DFA First State: The result of “q0 epsilon clouser”, which is {q0,q1,q2}, will be the initial state of the DFA. DFA with its initial state is given below
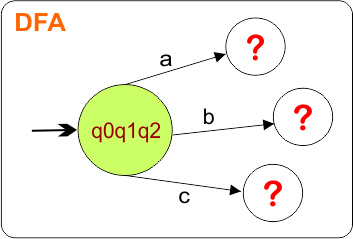The DFA transition table with its initial state is given below
In a DFA, we need to determine the transition for each input symbol at every state.
Step 02: Identify Transitions for each input symbol at every state
According to the transition rule of Epsilon NFA to DFA conversion, let’s start finding the transitions
Step 2.1: Identify Transitions for the Initial state ” {q0,q1,q2}”
Transition For input “a”
- δ {(q0,q1,q2), a} = ε Closure { δ(q0,a) U δ(q1,a) U δ(q2,a)
- δ {(q0,q1,q2), a} = ε Closure { q0 U ϕ U ϕ}
- δ {(q0,q1,q2), a} = ε Closure { q0 }
- δ {(q0,q1,q2), a} = {q0,q1,q2}
Transition For input “b”
- δ {(q0,q1,q2), b} = ε Closure { δ(q0,b) U δ(q1,b) U δ(q2,b)}
- δ {(q0,q1,q2), b} = ε Closure { ϕ U q1 U ϕ}
- δ {(q0,q1,q2), b} = ε Closure { q1 }
- δ {(q0,q1,q2), b} = {q1,q2}
Transition For input “c”
- δ {(q0,q1,q2), c} = ε Closure { δ(q0,c) U δ(q1,c) U δ(q2,c)}
- δ {(q0,q1,q2), c} = ε Closure { ϕ U ϕ U q2 }
- δ {(q0,q1,q2), c} = ε Closure { q2 }
- δ {(q0,q1,q2), c} = {q2}
The DFA transition table is updated as below
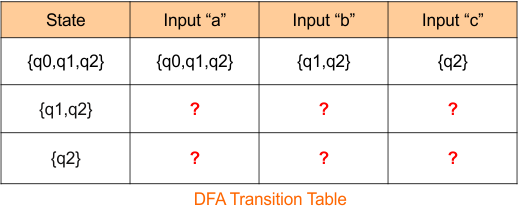
The DFA Diagram is updated as given below.
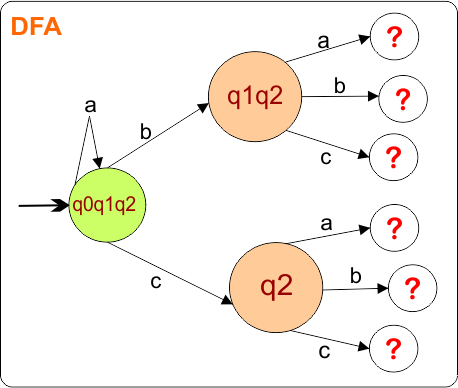
Now, we need to find a transition for state {q1,q2}, and {q2} for three input symbols “a”, “b”, and “c”.
Step 2.2: Identify Transitions for the state “{q1,q2}”
Transition For input “a”
- δ {(q1,q2), a} = ε Closure {δ(q1,a) U δ(q2,a)
- δ {(q1,q2), a} = ε Closure {ϕ U ϕ}
- δ {(q1,q2), a} = ε Closure { ϕ }
- δ {(q1,q2), a} = { ϕ }
Transition For input “b”
- δ {(q1,q2), b} = ε Closure {δ(q1,b) U δ(q2,b)}
- δ {(q1,q2), b} = ε Closure {q1 U ϕ}
- δ {(q1,q2), b} = ε Closure { q1 }
- δ {(q1,q2), b} = {q1,q2}
Transition For input “c”
- δ {(q1,q2), c} = ε Closure {δ(q1,c) U δ(q2,c)}
- δ {(q1,q2), c} = ε Closure { ϕ U q2 }
- δ {(q1,q2), c} = ε Closure { q2 }
- δ {(q1,q2), c} = {q2}
The DFA transition table is updated as below
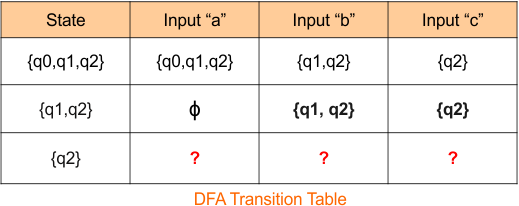
The DFA Diagram is updated as given below.
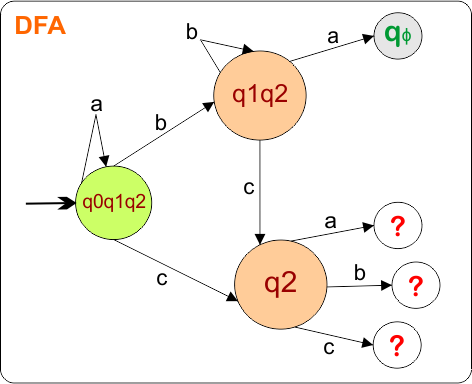
Now, we need to find a transition for state {q2}, and {qϕ} for three input symbols “a”, “b”, and “c”.
Step 2.3: Identify Transitions for the state “{q2}”
Transition For input “a”
- δ {q2, a} = ε Closure {δ(q2,a)
- δ {q2, a} = ε Closure {ϕ}
- δ {q2, a} = { ϕ }
Transition For input “b”
- δ {(q2), b} = ε Closure {δ(q2,b)}
- δ {(q2), b} = ε Closure {ϕ}
- δ {(q2), b} = {ϕ}
Transition For input “c”
- δ {q2, c} = ε Closure {δ(q2,c)}
- δ {q2, c} = ε Closure {q2 }
- δ {(q2), c} = {q2}
The DFA transition table is updated as below
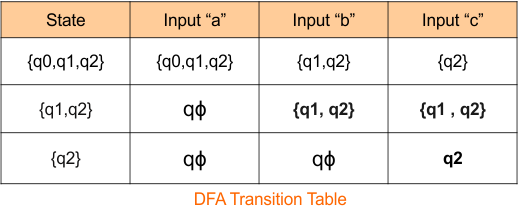
The DFA Diagram is updated as given below.
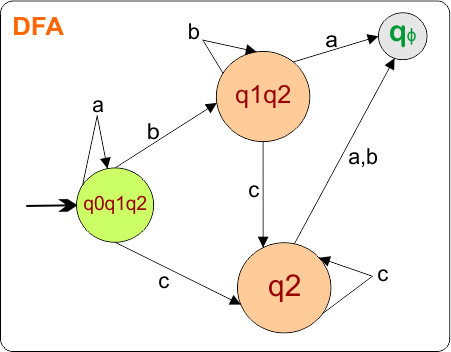
Now, we need to find a transition for state {qϕ} for three input symbols “a”, “b”, and “c”.
Step 2.4: Identify Transitions for the state “qϕ “
qϕ transitions for all input symbols will always self-loop (“qϕ “). The DFA transition table is updated as follows
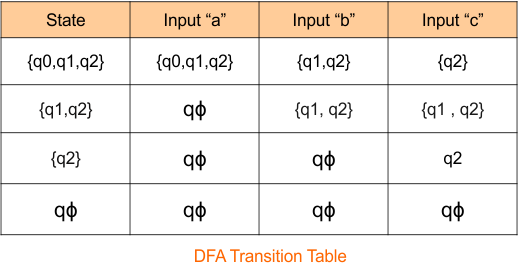
The DFA Diagram is updated as given below.
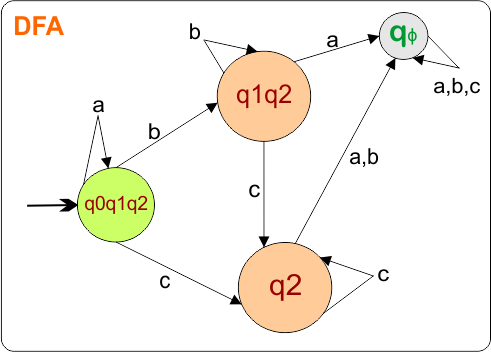
DFA condition for transitions is completed, no state remains for its transition. Now mark only the final states using a double circle symbol.
Step 03: Identify the Final States
In the given epsilon NFA, the state q2 was the final state. Therefore, all states in the DFA that include state “q2” are final. So, DFA with its Final states is given below
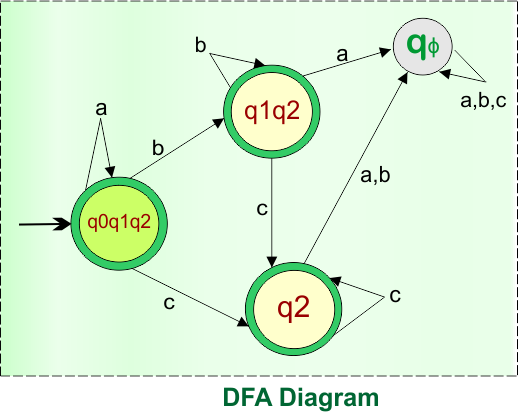
Thus, the above DFA is now complete and is equivalent to the given epsilon NFA in Example 4. The transition table of this DFA is given below
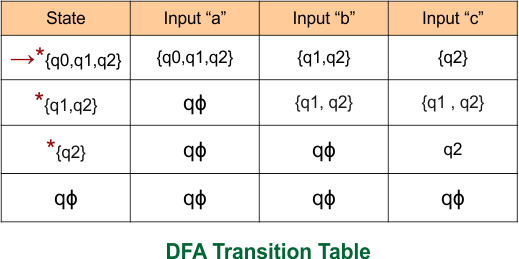
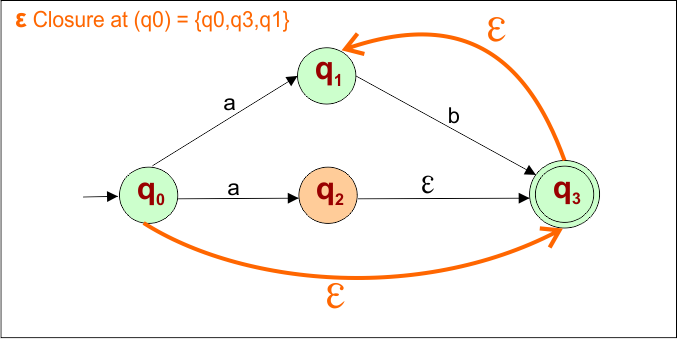
Example 05: Epsilon NFA to DFA
Here is the given NFA, which needs to be converted into a DFA
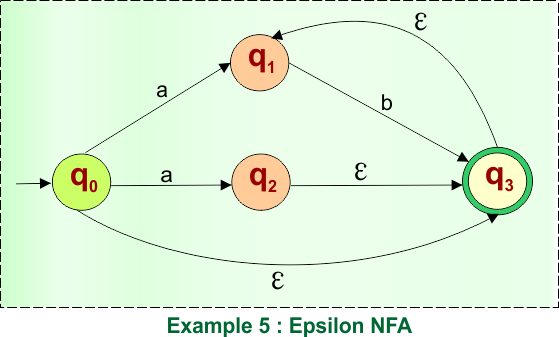
Step 01: Find the Epsilon closure of “q0”
The epsilon closure of state “q0” in the given epsilon NFA example includes states “q0”, “q3”, and “q1”, as we can reach these states only using epsilon transitions.
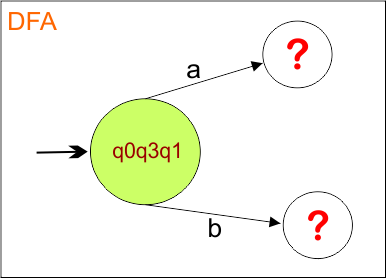
DFA First State: The result of “q0 epsilon clouser”, which is {q0,q3,q1}, will be the initial state of the DFA. DFA with its initial state is given below
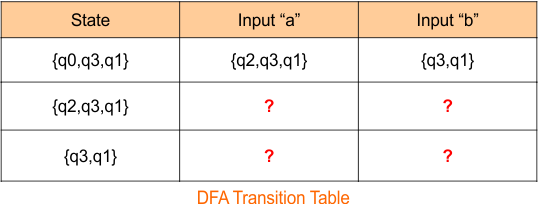
The DFA transition table with its initial state is given below
In a DFA, we need to determine the transition for each input symbol at every state.
Step 02: Identify Transitions for each input symbol at every state
According to the transition rule of Epsilon NFA to DFA conversion, let’s start finding the transitions
Step 2.1: Identify Transitions for the Initial state “q0q3q1”
Transition For input “a”
- δ {(q0,q3,q1), a} = ε Closure { δ(q0,a) U δ(q3,a) U δ(q1,a)}
- δ {(q0,q3,q1), a} = ε Closure { q1,q2 U ϕ U ϕ}
- δ {(q0,q3,q1), a} = ε Closure { q1,q2 }
- δ {(q0,q3,q1), a} = ε Closure { q1} U ε Closure { q2}
- δ {(q0,q3,q1), a} = { q1 } U { q2, q3, q1}
- δ {(q0,q3,q1), a} = { q2, q3, q1}
Transition For input “b”
- δ {(q0,q3,q1), b} = ε Closure { δ(q0,b) U δ(q3,b) U δ(q1,b)}
- δ {(q0,q3,q1), b} = ε Closure { ϕ U ϕ U q3}
- δ {(q0,q3,q1), b} = ε Closure { q3 }
- δ {(q0,q3,q1), b} = {q3,q1}
The DFA transition table is updated as follows
The DFA Diagram is updated as given below.
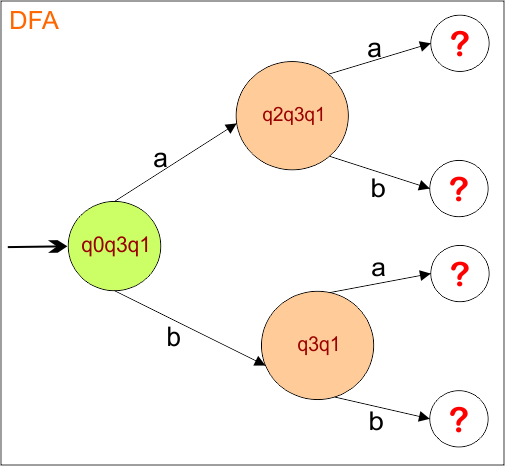
Now, we need to find a transition for state {q2,q3,q1} and {q3,q1} for both input symbols “a” and “b”.
Step 2.2: Identify Transitions for the state “q2q3q1”
Transition For input “a”
- δ {(q2,q3,q1), a} = ε Closure { δ(q2,a) U δ(q3,a) U δ(q1,a)}
- δ {(q2,q3,q1), a} = ε Closure { ϕ U ϕ U ϕ}
- δ {(q2,q3,q1), a} = ε Closure { ϕ }
- δ {(q2,q3,q1), a} = { ϕ }
Transition For input “b”
- δ {(q2,q3,q1), b} = ε Closure { δ(q2,b) U δ(q3,b) U δ(q1,b)}
- δ {(q2,q3,q1), b} = ε Closure { ϕ U ϕ U q3}
- δ {(q2,q3,q1), b} = ε Closure { q3 }
- δ {(q2,q3,q1), b} = {q3,q1}
The DFA transition table is updated as below
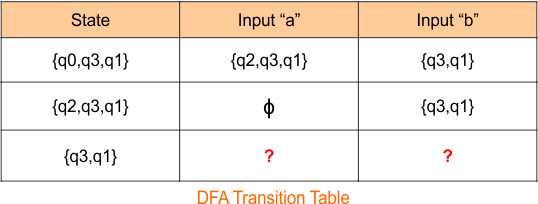
The DFA Diagram is updated as given below.
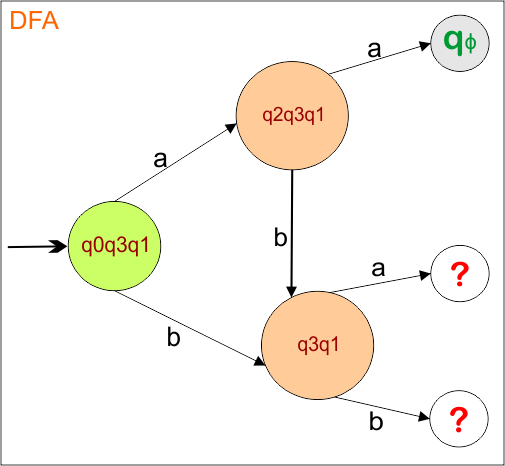
Now, we need to find a transition for state “q3q1” and “qϕ” for both input symbols “a” and “b”.
Step 2.3: Identify Transitions for the state “q3q1”
Transition For input “a”
- δ {(q3,q1), a} = ε Closure {δ(q3,a) U δ(q1,a)}
- δ {(q3,q1), a} = ε Closure { ϕ U ϕ}
- δ {(q3,q1), a} = ε Closure { ϕ }
- δ {(q3,q1), a} = { ϕ }
Transition For input “b”
- δ {(q3,q1), b} = ε Closure { δ(q3,b) U δ(q1,b)}
- δ {(q3,q1), b} = ε Closure { ϕ U q3}
- δ {(q3,q1), b} = ε Closure { q3 }
- δ {(q3,q1), b} = {q3,q1}
The DFA transition table is updated as follows
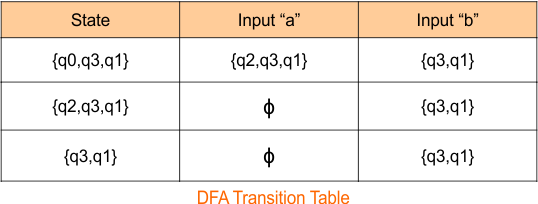
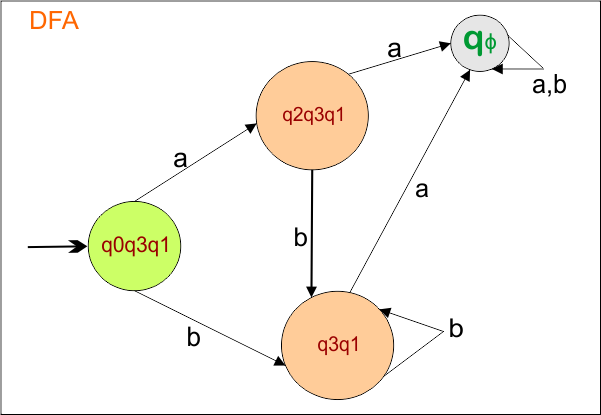
The DFA Diagram is updated as given below.
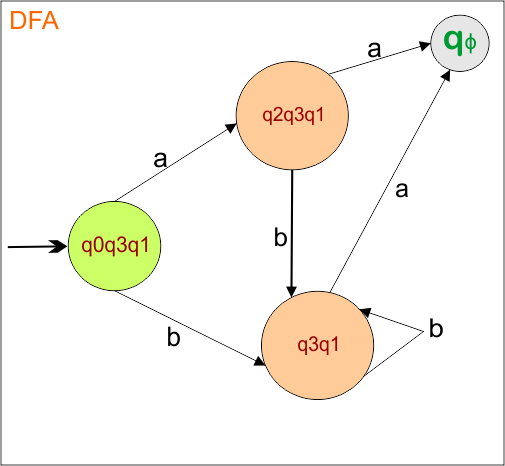
Now, we need to find a transition for state “qϕ ” for both input symbols “a” and “b”.
Step 2.4: Identify Transitions for the state “qϕ “
qϕ transitions for all input symbols will always self-loop (“qϕ “). The DFA transition table is updated as follows
Here is the transition Table of the above NFA
DFA condition for transitions is completed, no state remains for its transition. Now mark only the final states using a double circle symbol.
Step 03: Identify the Final States
In the given epsilon NFA, the state “q3” was the final state. Therefore, all states in the DFA that include state “q3” are final. So, DFA with its Final states is given below
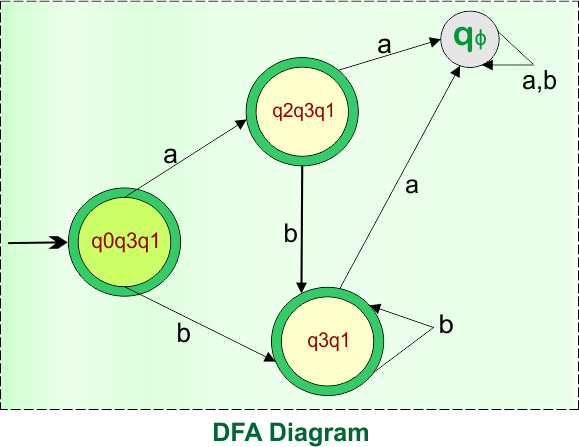
Thus, the above DFA is complete and equivalent to the given epsilon NFA in example 5. The transition table of this DFA is given below
Example 06: Epsilon NFA to DFA
Here is the given NFA, which needs to be converted into a DFA
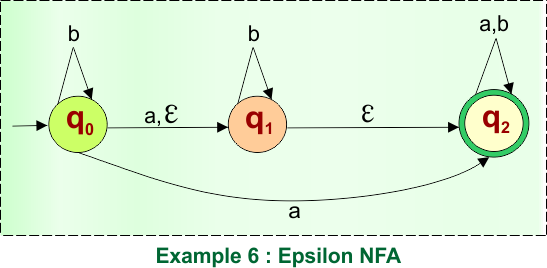
Step 01: Find the Epsilon closure of “q0”
The epsilon closure of state “q0” in the given epsilon NFA example includes states “q0”, “q1”, and “q2”, as we can reach these states only using epsilon transitions.
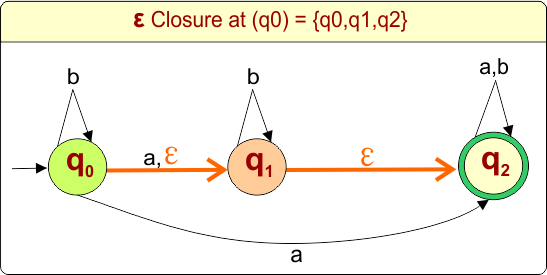
DFA First State: The result of “q0 epsilon clouser”, which is {q0,q1,q2}, will be the initial state of the DFA. DFA with its initial state is given below
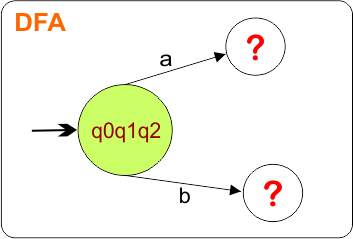
The DFA transition table with its initial state is given below
In a DFA, we need to determine the transition for each input symbol at every state.
Step 02: Identify Transitions for each input symbol at every state
According to the transition rule of Epsilon NFA to DFA conversion, let’s start finding the transitions
Step 2.1: Identify Transitions for the Initial state “q0q1q2”
Transition For input “a”
- δ {(q0,q1,q2), a} = ε Closure { δ(q0,a) U δ(q1,a) U δ(q2,a)}
- δ {(q0,q1,q2), a} = ε Closure { q1 U ϕ U q2}
- δ {(q0,q1,q2), a} = ε Closure { q1,q2 }
- δ {(q0,q1,q2), a} = ε Closure { q1} U ε Closure { q2}
- δ {(q0,q1,q1), a} = { q1,q2 } U { q2}
- δ {(q0,q1,q2), a} = { q1,q2}
Transition For input “b”
- δ {(q0,q1,q2), b} = ε Closure { δ(q0,b) U δ(q1,b) U δ(q2,b)}
- δ {(q0,q1,q2), b} = ε Closure { q0 U q1 U q2}
- δ {(q0,q1,q2), b} = ε Closure { q0,q1,q2 }
- δ {(q0,q1,q2), b} = ε Closure { q0} U ε Closure { q1} U ε Closure { q2}
- δ {(q0,q1,q1), b} = { q0,q1,q2 } U { q1,q2} U {q2}
- δ {(q0,q1,q2), b} = { q0,q1,q2}
The DFA transition table is updated as follows
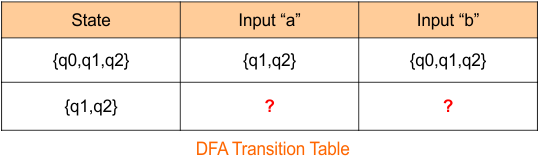
The DFA Diagram is updated as given below.
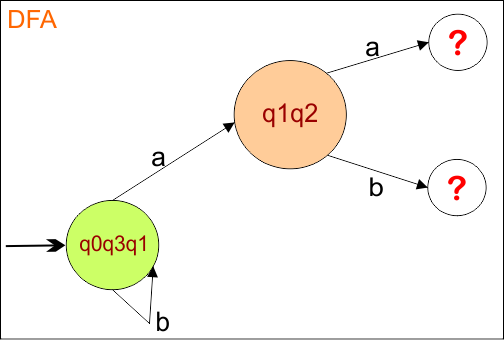
Now, we need to find a transition for state “q1q2” for both input symbols “a” and “b”.
Step 2.2: Identify Transitions for the state “q1q2”
Transition For input “a”
- δ {(q1,q2), a} = ε Closure {δ(q1,a) U δ(q2,a)}
- δ {(q1,q2), a} = ε Closure { ϕ U q2}
- δ {(q1,q2), a} = ε Closure { q2 }
- δ {(q1,q2), a} = { q2}
Transition For input “b”
- δ {(q1,q2), b} = ε Closure {U δ(q1,b) U δ(q2,b)}
- δ {(q1,q2), b} = ε Closure { q1 U q2}
- δ {(q1,q2), b} = ε Closure { q1,q2 }
- δ {(q1,q2), b} = ε Closure { q1} U ε Closure { q2}
- δ {(q1,q1), b} = { q1,q2} U {q2}
- δ {(q1,q2), b} = { q1,q2}
The DFA transition table is updated as follows
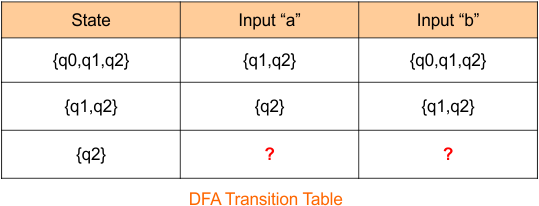
The DFA Diagram is updated as given below.
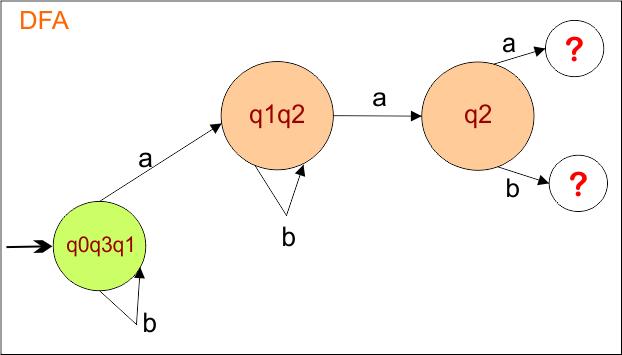
Now, we need to find a transition for state “q2” for both input symbols “a” and “b”.
Step 2.3: Identify Transitions for the state “q2”
Transition For input “a”
- δ {q2, a} = ε Closure {δ(q2,a)}
δ {q2, a} = ε Closure {q2}
δ {q2, a} = { q2}
Transition For input “b”
- δ {q2, b} = ε Closure {δ(q2,b)}
δ {q2, b} = ε Closure {q2}
δ {q2, b} = {q2 }
The DFA transition table is updated as follows
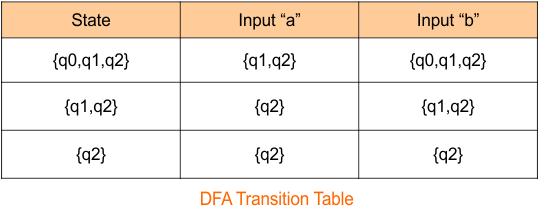
The DFA Diagram is updated as given below.
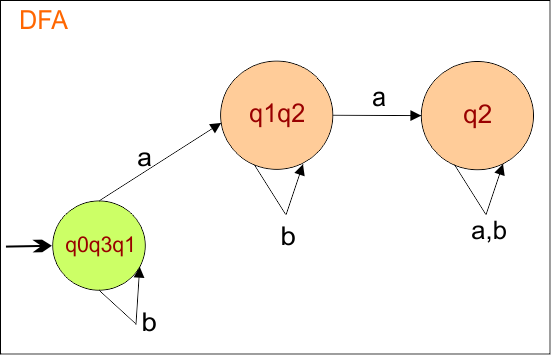
Now, we need to find a transition for state “q2” for both input symbols “a” and “b”.
Once the DFA condition for transitions is completed, no state remains for its transition. Now, mark only the final states using a double circle symbol.
Step 03: Identify the Final States
In the given epsilon NFA, the state “q3” was the final state. Therefore, all states in the DFA that include state “q3” are final. So, DFA with its Final states is given below
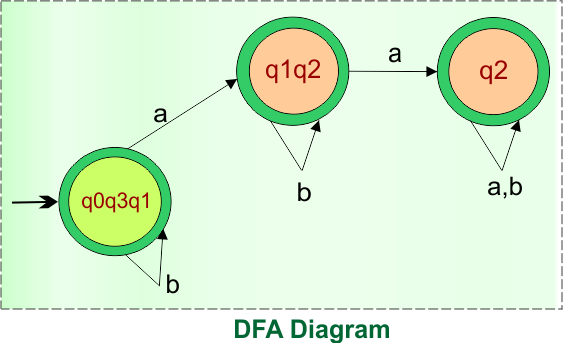
Thus, the above DFA is complete and equivalent to the given epsilon NFA in example 5. The transition table of this DFA is given below
