Ambiguity in Context-Free Grammar

Ambiguity in a context-free grammar occurs when a single string can be generated by the grammar in more than one way, resulting in multiple parse trees, leftmost derivations, or rightmost derivations. A context-free grammar is said to be ambiguous if at least one string in its language has two or more distinct derivation trees.

Note: We use a general approach to identify ambiguity in Context-free grammar as there is still no algorithm that checks it.

Based on the number of derivation trees in TOC, Ambiguity Grammar is classified into two terms. One is ambiguous grammar, and the other is Unambiguous grammar.

1. Ambiguous Grammar

A grammar is said to be ambiguous grammar if any string generated by it produces more than one.

• Parse tree (syntax tree)
• Or leftmost derivation
• Or rightmost derivation

Examples of Ambiguous Grammar

Example 01: Check whether the following grammar is ambiguous or not for string w = ab

S → A / B

A → aAb / ab

B → abB / ∈

Solution: Now, we draw more than one parse tree to get the string w = ab.

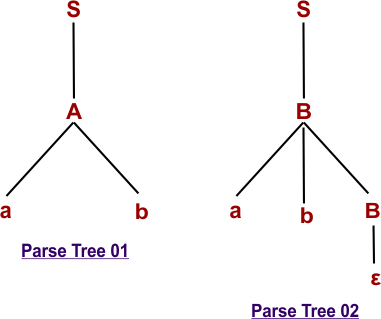
The original string (w =ab)  can derived through two different parse trees. So,  the given grammar is ambiguous.

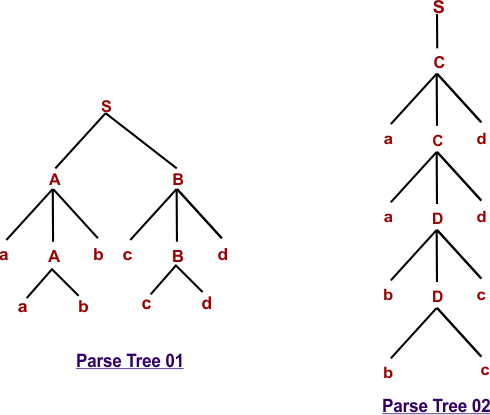
Example-02: Check whether the following grammar is ambiguous or not for string w = aabbccdd

S → AB / C

A → aAb / ab

B → cBd / cd

C → aCd / aDd

D → bDc / bc

Solution: Now we draw more than one parse tree to get string w = aabbccdd.

The original string (w =aabbccdd)  can derived through two different parse trees. So,  the given grammar is ambiguous.

2. Unambiguous Grammar

A grammar is said to be unambiguous grammar if every string generated by it produces exactly one.

• Parse tree
• Or syntax tree
• Or leftmost derivation
• Or rightmost derivation

Note: So, If we try to derive more than one tree of unambiguous grammar, then all trees will be similar

Examples of Unambiguous Grammar

Example 01: For string “aab” the following grammar is unambiguous

S → AB  

A → Aa | a  

B → b  

Solution: Let’s draw the leftmost and rightmost derivations of the above grammar to get the string “aab.”

Because all parse trees, syntax trees, and left or right derivations will be similar for the above grammar of string “aab.” So, the  above grammar is unambiguous.

Example 02: For string “id+id*id,” the following grammar is unambiguous

• E → E + T  
• E → T  
• T → T * F  
• T → F  
• F → id  

Solution: Because all parse trees, syntax trees, and left or right derivations will be similar for the above string grammar “id+id*id.” As given below

Removal of Ambiguity from CFG

Conversion from an ambiguous grammar into an unambiguous grammar is not always possible. Several methods are employed to eliminate ambiguity from the CFG. Some common methods are given below.

• By fixing the grammar
• By adding the precedence rules
• By adding grouping rules
• By using semantics