Leftmost Derivation in Automata

Getting a string by expanding the leftmost nonterminal at each step is called a leftmost derivation in Automata.

  • The representation of leftmost derivation in a tree is called a leftmost derivation tree.
  • We read the given input string (W) from left to right in the leftmost derivation tree.

Example of Leftmost Derivation

Consider the following production rules for the grammar (G)

S → xB / yA

S → xS / yAA / x

B → yS / xBB / y

Consider a string W = xxxyyxyyyx

Let us derive the given string (W= xxxyyxyyyx) by using given grammar production rules. We will also draw the derivation tree of each step, as shown below.

Leftmost Derivation and Tree

Let us see derivation through production rules and their tree as given below.

Step 01: S   → xB                    (W=xB)

Leftmost Derivation Step 01

Step 02: W= xxBB                   (Using B → xBB)

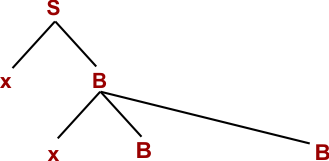
Leftmost Derivation Step 02

Step 03: W= xxxBBB                (Using B → xBB)

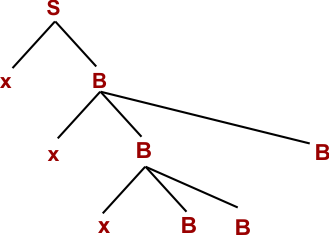
Leftmost Derivation Step 03

Step 04: W= xxxyBB                (Using B → y)

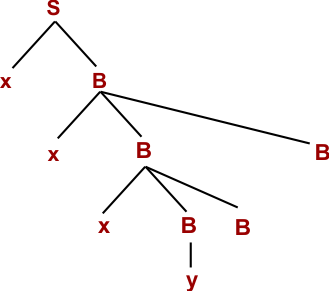
Leftmost Derivation Step 04

Step 05: W= xxxyyB                (Using B → y)

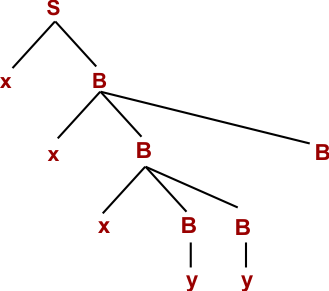
Leftmost Derivation Step 05

Step 06: W= xxxyyxBB            (Using B → xBB)

Leftmost Derivation Step 06

Step 07: W= xxxyyxyB            (Using B → y)

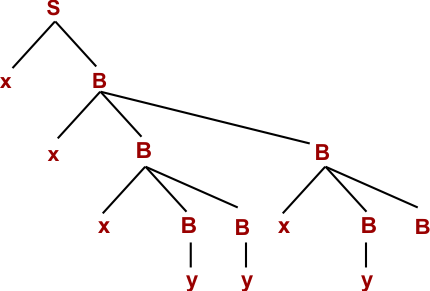
Leftmost Derivation Step 07

Step 08: W= xxxyyxyyS          (Using B → yS)

Leftmost Derivation Step 08

Step 09: W= xxxyyxyyyA        (Using S → yA)

Leftmost Derivation Step 09

Step 10: W= xxxyyxyyyx        (Using A → x)

 

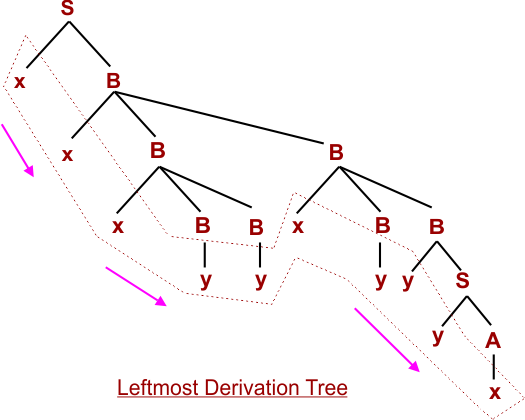
Leftmost Derivation Step 10

Hence the given string (W= xxxyyxyyyx) is derived through leftmost derivation. So, the given string belongs to the Given Grammar (G).