Regular Expression In TOC
Regular Expression in TOC is a powerful mathematical tool used to define regular languages, which are recognized by Finite Automata. They are similar to arithmetic, logic, and Boolean expressions in representation but differnt in their operation and purpose.
- Regular expressions generate sets of strings (finite or infinite in number) that always represent a unique and specific regular language.
- Each of these regular languages can be recognized and accepted by a finite automata.
The following figures show the above description

The main uses of regular expressions in TOC are
- Pattern Recognition: Represent patterns that can be recognized by finite automata (DFA and NFA).
- Compiler Design: Used in lexical analysis to tokenize input strings during compilation.
- Automata Conversion: Enable conversion between regular expressions and finite automata for language recognition.
- Theoretical Analysis: Help analyze and prove properties of languages within formal language theory.
Let’s Explain Various Categories of Regular Expressions in the TOC. These categories include Basic, start with, end with, and start and end with some characters. Let’s see more than 40 examples that fall under these categories. Each example contains the following
- Derived strings from a given regular expression
- Specific Language is extracted from the given regular expression
- Deterministic Finite Automata (DFA) for a given expression.
Let’s start with the first category with its 21 examples
Category 1: Basic Regular Expressions
Here’s a table that explains the basic components of regular expressions. The first column shows the expression, and the second explains its meaning.
| Sr. | Regular Expression | Explanation |
|---|---|---|
| 1 | a |
Only a single character "a". |
| 2 | ab |
Sequence "a" followed by "b". |
| 3 | (a+b) |
Either "a" or "b". |
| 4 | (a)* |
Zero (ε) or more occurrences of "a". |
| 5 | (ab)* |
Zero (ε) or more repetitions of the sequence “ab". |
| 6 | (a+b)* |
Zero (ε) or more symbols from the alphabet {a,b} of any length, any order. |
| 7 | (a)+ |
One or more occurrences of "a". |
| 8 | (ab)+ |
One or more repetitions of the sequence "ab". |
| 9 | (a+b)+ |
One or more symbols chosen from "a" or "b". |
| 10 | (10+1)* |
Zero (ε) or more repetitions of "10" or "1". |
| 11 | (01+10+1)* |
Zero (ε) or more repetitions of "01", "10", or "1". |
| 12 | (a+b+c+d)* |
Zero (ε) or more symbols chosen from "a", "b", "c", or "d". |
| 13 | (a+b+c+d)+ |
One or more symbols chosen from "a", "b", "c", or "d". |
| 14 | (ab+bb+cc+dd)* |
Zero (ε) or more repetitions of "ab", "bb", "cc", or "dd". |
| 15 | 101 + (0+1)*1 |
Either "101" or any combination of 0s and "1s” ending in "1". |
| 16 | 11 + 00 + 0 + 10* |
Either "11", "00", a single "0", or "1" followed by zero or more "0s”. |
| 17 | 1(0 + 11) + 0(00 + 1) |
Either "1" followed by "0" or "11", or "0" followed by "00" or "1". |
| 18 | ba + (aa + b)* |
Either "ba" or any number of repetitions of "aa" or "b". |
| 19 | aa + ba + (aa + b)* |
Either "aa", "ba", or any number of repetitions of "aa" or "b". |
| 20 | (00)*(0 + 1) + (1)* |
Zero (ε) or more "00"s followed by 0 or 1, or any number of "1s”. |
| 21 | (001)* + (00) |
Zero (ε) or more repetitions of "001", or exactly "00". |
Example 1.1: Regular Expression = a
Step 01: Find the strings that can be derived from the given expression RE = a. The following figure shows all possible strings that can be derived from RE = a
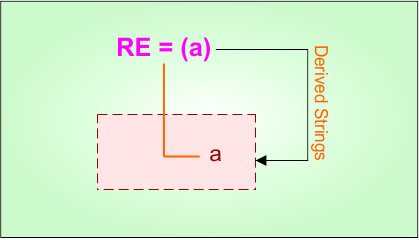
Note: All strings derived from step 01 are accepted by the DFA, which is designed in step 02.
Step 02: Possible strings, Language, and DFA for RE = a are given in the following diagram
Example 1.2: Regular Expression = ab
Step 01: Find the strings that can be derived from the given expression RE = “ab”.. The following figure shows all possible strings that can be derived from RE = “ab”.
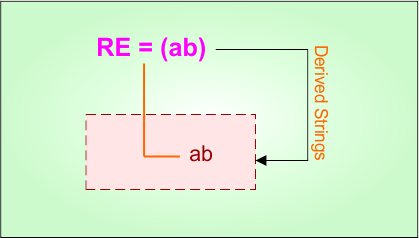
Note Again: All strings derived from step 01 are accepted by the DFA, which is designed in step 02.
Step 02: Possible strings, Language, and DFA for RE = “ab” are given in the following diagram

Example 1.3: Regular Expression = (a+b)
Step 01: Find the strings that can be derived from the given expression RE = (a+b). The following figure shows all possible strings that can be derived from RE = (a+b).
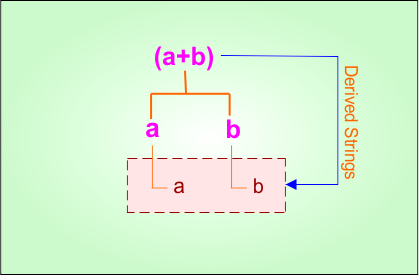
Step 02: Possible strings, Language, and DFA for RE = (a+b) are given in the following diagram
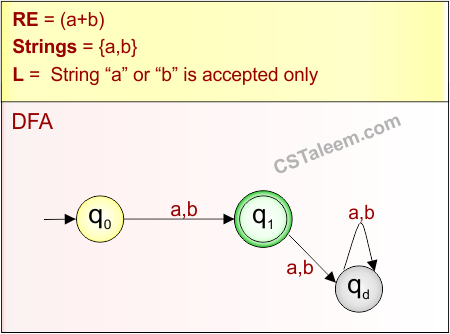
Example 1.4: Regular Expression = (a)*
Step 01: Find the strings that can be derived from the given expression RE = (a)*. The following figure shows all possible strings that can be derived from RE = (a)*
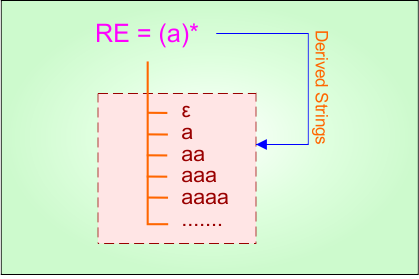
Step 02: Possible strings, Language, and DFA for RE = (a)* are given in the following diagram

Example 1.5: Regular Expression = (ab)*
Step 01: Find the strings that can be derived from the given expression RE = (ab)*. The following figure shows all possible strings that can be derived from RE = (ab)*.
 Step 02: Possible strings, Language, and DFA for RE = (ab)* are given in the following diagram
Step 02: Possible strings, Language, and DFA for RE = (ab)* are given in the following diagram

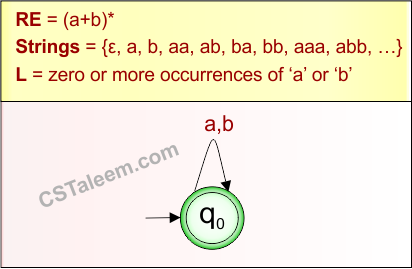
Example 1.6: Regular Expression = (a+b)*
Step 01: Find the strings that can be derived from the given expression RE = (a+b)*. The following figure shows all possible strings that can be derived from RE = (a+b)*

Step 02: Possible strings, Language and DFA for RE = (a+b)* are given in the following diagram
Example 1.7: Regular Expression = a+
Step 01: Find the strings that can be derived from the given expression RE = a+. The following figure shows all possible strings that can be derived from RE = a+
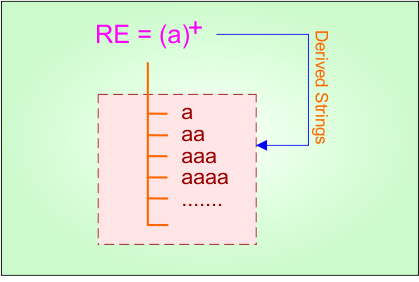
Step 02: Possible strings, Language, and DFA for RE = a+ are given in the following diagram

Example 1.8: Regular Expression = (ab)+
Step 01: Find the strings that can be derived from the given expression RE = (ab)+. The following figure shows all possible strings that can be derived from RE = (ab)+.
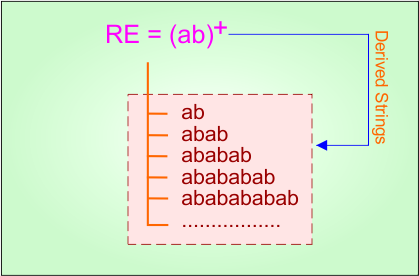
Step 02: Possible strings, Language, and DFA for RE = (ab)+ are given in the following diagram
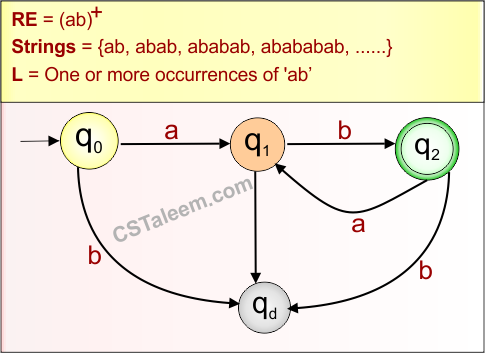
Example 1.9: Regular Expression = (a+b)+
Step 01: Find the strings that can be derived from the given expression RE = (a+b)+. The following figure shows all possible strings that can be derived from RE = (a+b)+
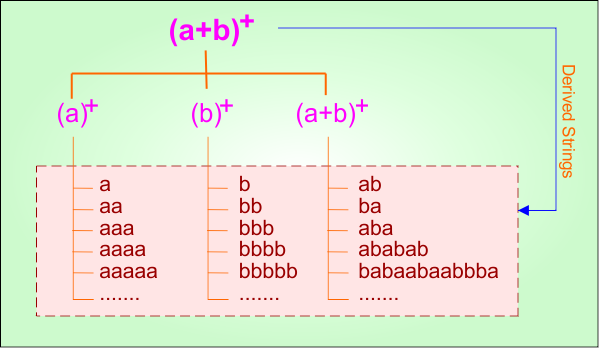
Step 02: Possible strings, Language and DFA for RE = (a+b)+ are given in the following diagram
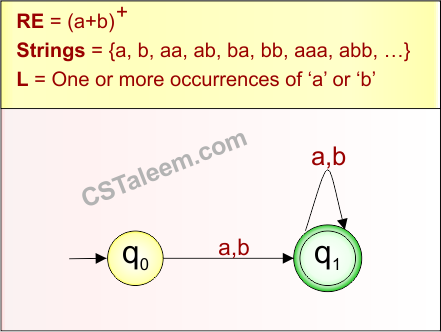
Example 1.10: Regular Expression = (10+1)*
Step 01: Find the strings that can be derived from the given expression RE = (10+1)*. The following figure shows all possible strings that can be derived from RE = (10+1)*

Step 02: Possible strings, Language and DFA for RE = (10+1)* are given in the following diagram

Example 1.11: Regular Expression = (01+10+1)*
Step 01: Find the strings that can be derived from the given expression RE = (01+10+1)*. The following figure shows all possible strings which can be derived from RE = (01+10+1)*
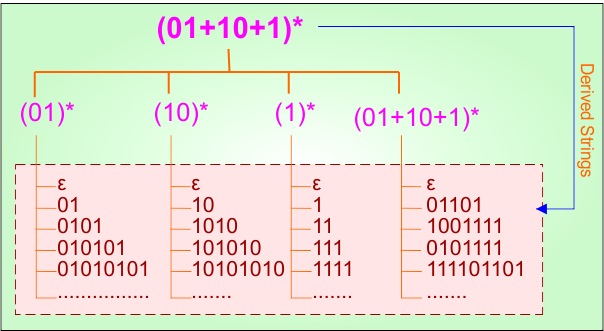
Step 02: Possible strings, Language and DFA for RE = (01+10+1)* are given in the following diagram
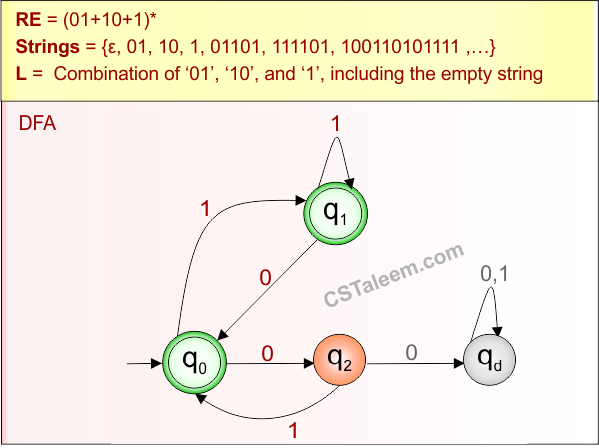
Example 1.12: Regular Expression = (a+b+c+d)*
Step 01: Find the strings that can be derived from the given expression RE = (a+b+c+d)*. The following figure shows all possible strings that can be derived from RE = (a+b+c+d)*
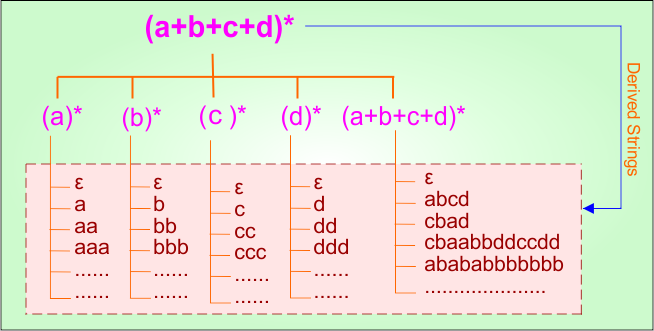
Step 02: Possible strings, Language and DFA for RE = (a+b+c+d)* are given in the following diagram
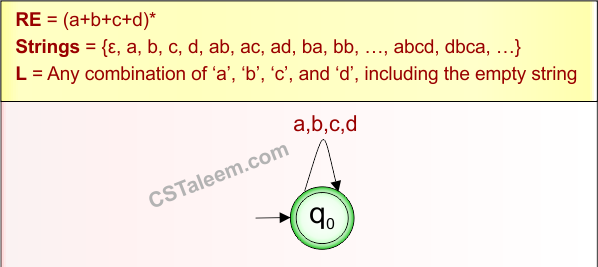
Example 1.13: Regular Expression = (a+b+c+d)+
Step 01: Find the strings that can be derived from the given expression RE = (a+b+c+d)+. The following figure shows all possible strings that can be derived from RE = (a+b+c+d)+
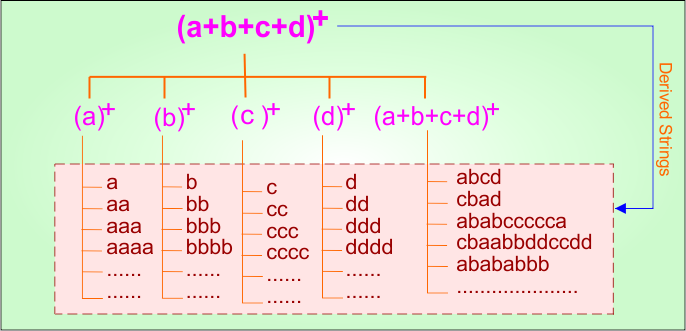
Step 02: Possible strings, Language and DFA for RE = (a+b+c+d)+ are given in the following diagram

Example 1.14: Regular Expression = (ab+bb+cc+dd)*
Step 01: Find the strings that can be derived from the given expression RE = (ab+bb+cc+dd)*. The following figure shows all possible strings that can be derived from RE = (ab+bb+cc+dd)*
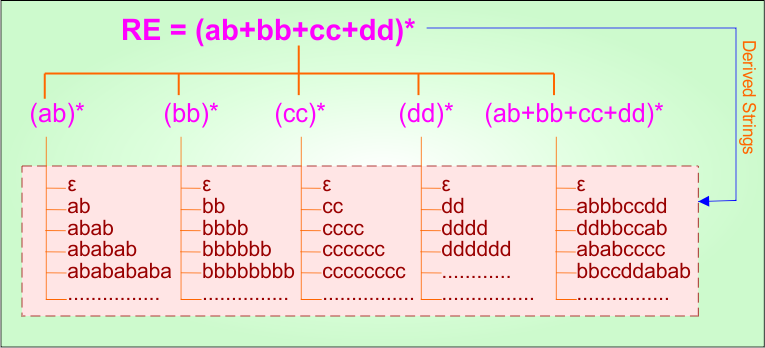
Step 02: Possible strings, Language and DFA for RE = (ab+bb+cc+dd)* are given in the following diagram
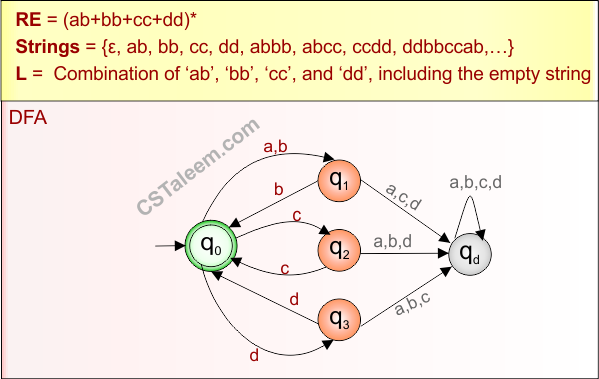
Example 1.15: Regular Expression = 101 + (0+1)*1
Step 01: Find the strings that can be derived from the given expression RE = 101 + (0+1)*1. The following figure shows all possible strings that can be derived from RE = 101 + (0+1)*1

Step 02: Possible strings, Language and DFA for RE = 101 + (0+1)*1 are given in the following diagram
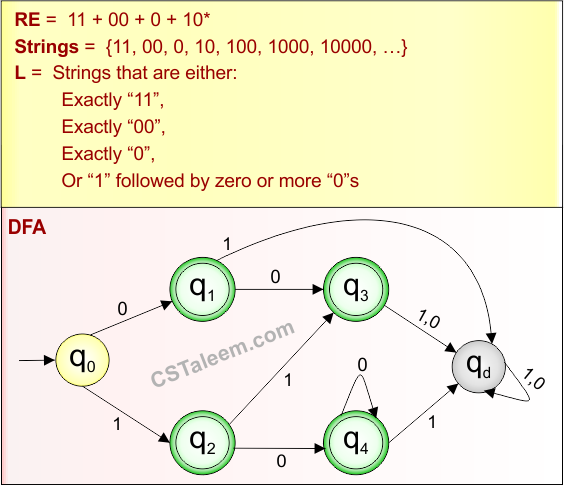
Example 1.16: Regular Expression = 11 + 00 + 0 + 10*
Step 01: Find the strings that can be derived from the given expression RE = 11 + 00 + 0 + 10*. The following figure shows all possible strings that can be derived from RE = 11 + 00 + 0 + 10*
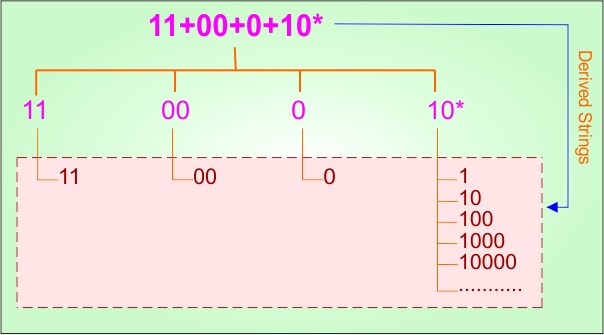
Step 02: Possible strings, Language and DFA for RE = 11 + 00 + 0 + 10* are given in the following diagram
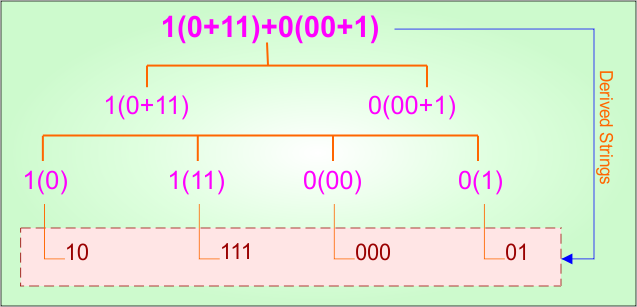
Example 1.17: Regular Expression = 1(0 + 11) + 0(00 + 1)
Step 01: Find the strings that can be derived from the given expression RE = 1(0 + 11) + 0(00 + 1). The following figure shows all possible strings that can be derived from RE = 1(0 + 11) + 0(00 + 1)
Step 02: Possible strings, Language and DFA for RE = 1(0 + 11) + 0(00 + 1) are given in the following diagram
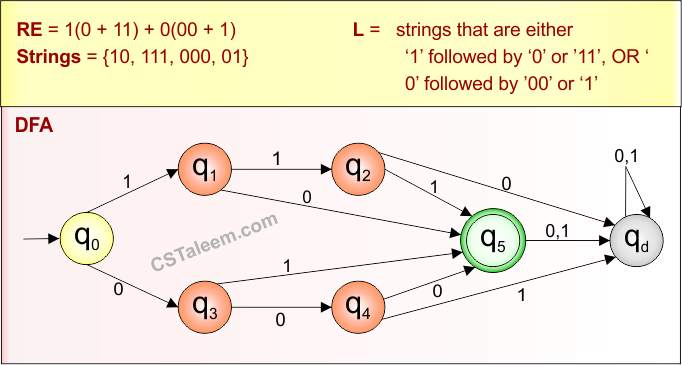
Example 1.18: Regular Expression = ba + (aa + b)*
Step 01: Find the strings that can be derived from the given expression RE = ba + (aa + b)*. The following figure shows all possible strings that can be derived from RE = ba + (aa + b)*
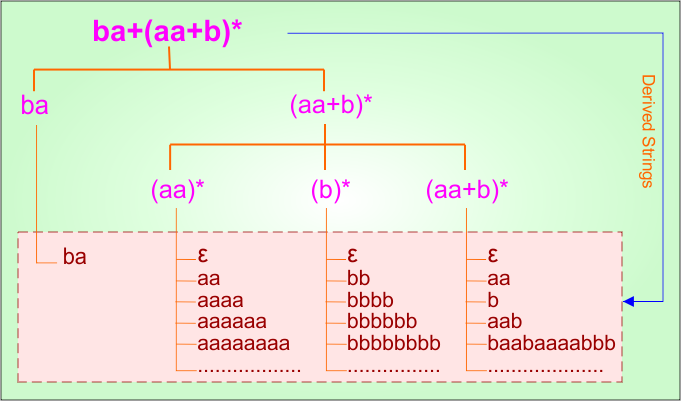
Step 02: Possible strings, Language and DFA for RE = ba + (aa + b)* are given in the following diagram
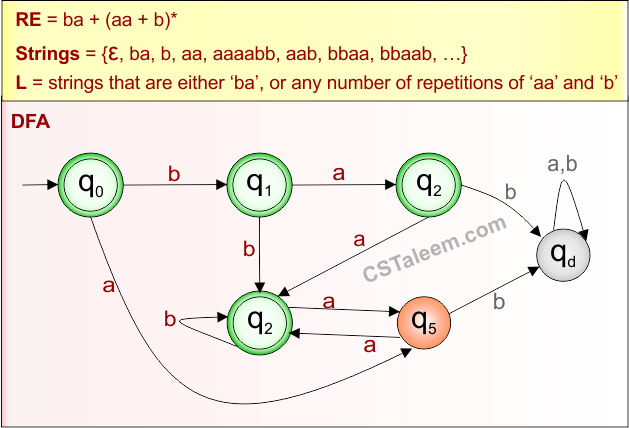
Example 1.19: Regular Expression = aa + ba + (aa + b)*
Step 01: Find the strings that can be derived from the given expression RE = aa + ba + (aa + b)*. The following figure shows all possible strings that can be derived from RE = aa + ba + (aa + b)*
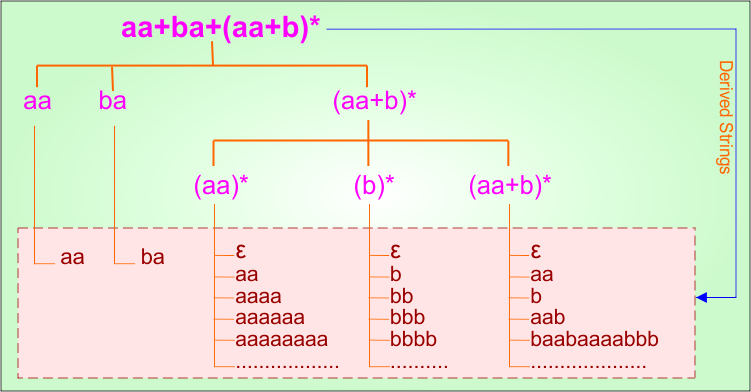
Step 02: Possible strings, Language and DFA for RE = aa + ba + (aa + b)* are given in the following diagram
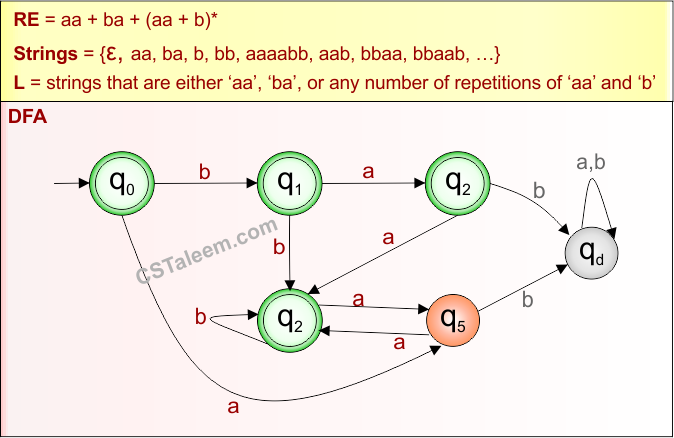
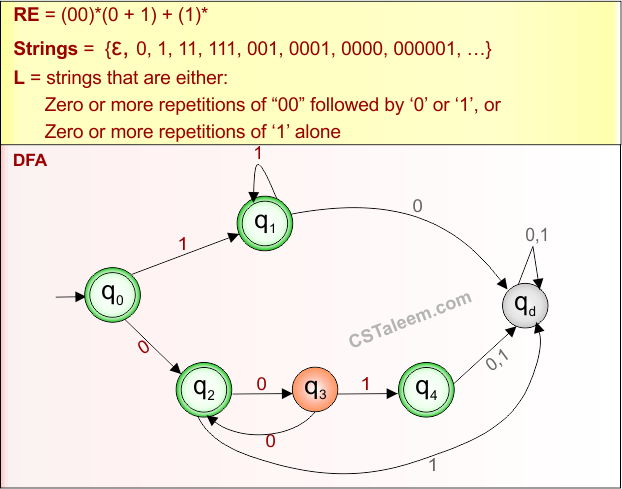
Example 1.20: Regular Expression = (00)*(0 + 1) + (1)*
Step 01: Find the strings that can be derived from the given expression RE = (00)*(0 + 1) + (1)*. The following figure shows all possible strings that can be derived from RE = (00)*(0 + 1) + (1)*
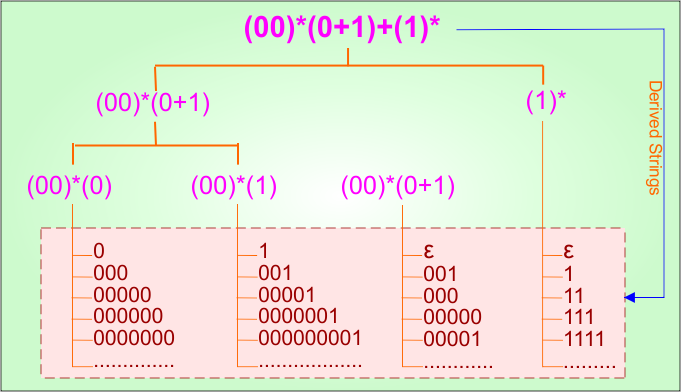
Step 02: Possible strings, Language and DFA for RE = (00)*(0 + 1) + (1)* are given in the following diagram
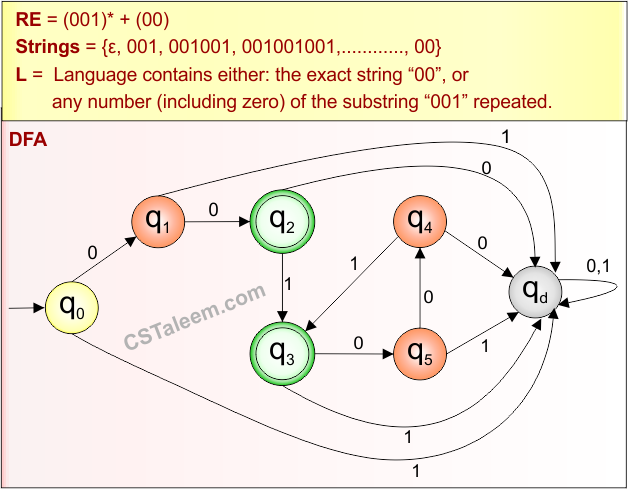
Example 1.21: Regular Expression = (001)* + (00)
Step 01: Find the strings that can be derived from the given expression RE = (001)* + (00). The following figure shows all possible strings that can be derived from RE = (001)* + (00)

Step 02: Possible strings, Language and DFA for RE = (001)* + (00) are given in the following diagram
Category 2: Start with Regular Expressions
Here’s a table that explains the second category (starts with) of regular expressions. The first column shows the expression, and the second explains its meaning.
| sr. | Regular Expression | Simple Explanation |
|---|---|---|
| 1 | a(a+b)* |
Starts with a, followed by any number (even zero) of as or bs in any order. |
| 2 | 101*(0+1)* |
Starts with 10, then zero or more repeats of 1, then zero or more mix of 0s and 1s. |
| 3 | bab(a+b)* |
Starts with bab, followed by zero or any number of as or bs . |
| 4 | aa(aba+bab)* |
Starts with aa, followed by zero or any number of the patterns aba or bab. |
| 5 | (a(bb)*)(a+b)* |
Starts with a, then zero or more bbs, then zero or any number of as or bs in any order. |
| 6 | 1(0+1)(00+11)* |
Starts with 1, then either 0 or 1, then zero or more repeats of 00 or 11. |
| 7 | a+b+c(ab+bb+cc)* |
One"a", One “b”, or starts with"cand then zero or more repeats of ab, bb, or cc patterns. |
| 8 | a+b+c+d(ab+bb+cc+dd)* |
One"a", One “b”, One “c” or starts with"dand then zero or more repeats of ab, bb, cc, or dd patterns. |
| 9 | aba(a+b)* + bab(a+b)* |
Either starts with aba or bab, followed by zero or any number of as or bs |
Example 2.1: Regular Expression = a(a+b)*
Step 01: Find the strings that can be derived from the given expression RE = a(a+b)*. The following figure shows all possible strings that can be derived from RE = a(a+b)*
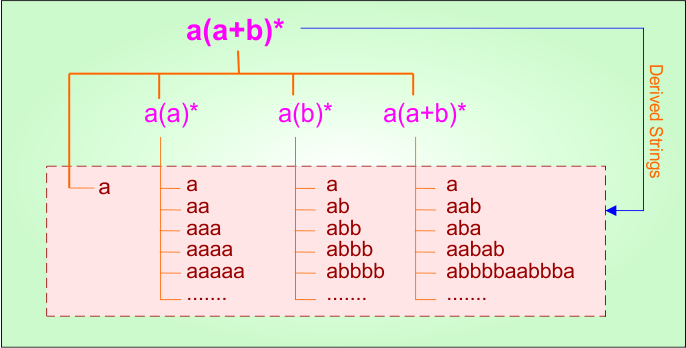
Step 02: Possible strings, Language and DFA for RE = a(a+b)* are given in the following diagram

Example 2.2: Regular Expression = 101*(0+1)*
Step 01: Find the strings that can be derived from the given expression RE = 101*(0+1)*. The following figure shows all possible strings that can be derived from RE = 101*(0+1)*
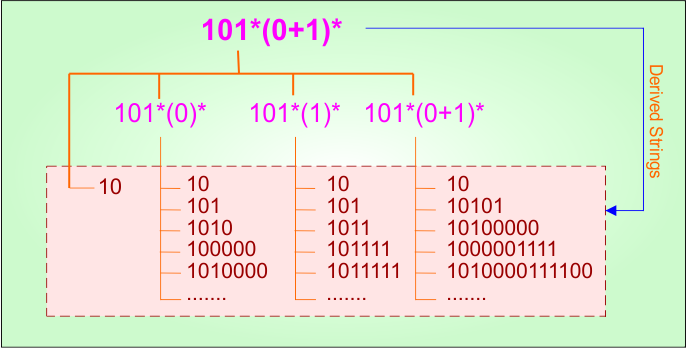
Step 02: Possible strings, Language and DFA for RE = 101*(0+1)* are given in the following diagram
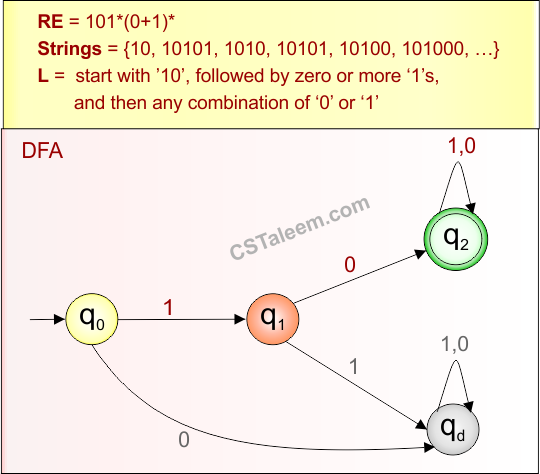
Example 2.3: Regular Expression = bab(a+b)*
Step 01: Find the strings that can be derived from the given expression RE = bab(a+b)*. The following figure shows all possible strings that can be derived from RE = bab(a+b)*
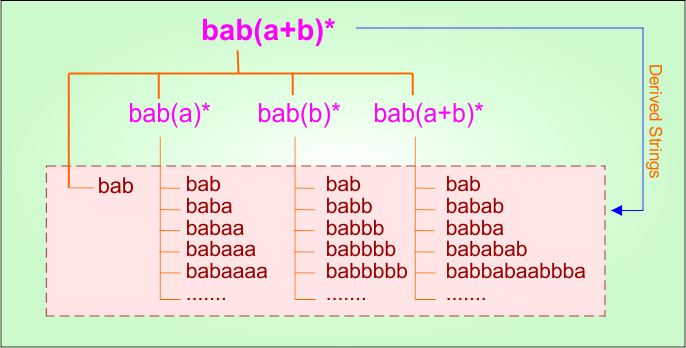
Step 02: Possible strings, Language and DFA for RE = bab(a+b)* are given in the following diagram

Example 2.4: Regular Expression = aa(aba+bab)*
Step 01: Find the strings that can be derived from the given expression RE = aa(aba+bab)*. The following figure shows all possible strings that can be derived from RE = aa(aba+bab)*
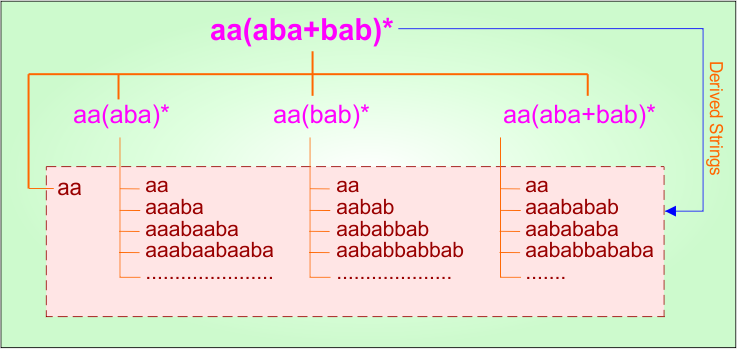
Step 02: Possible strings, Language and DFA for RE = aa(aba+bab)* are given in the following diagram

Example 2.5: Regular Expression = (a(bb)*)(a+b)*
Step 01: Find the strings that can be derived from the given expression RE = (a(bb)*)(a+b)*. The following figure shows all possible strings that can be derived from RE = (a(bb)*)(a+b)*
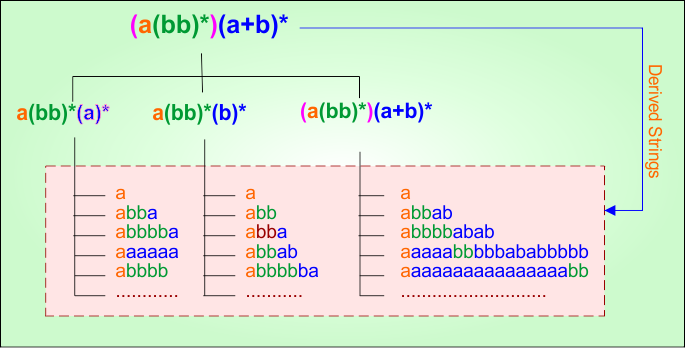
Step 02: Possible strings, Language and DFA for RE = (a(bb)*)(a+b)* are given in the following diagram

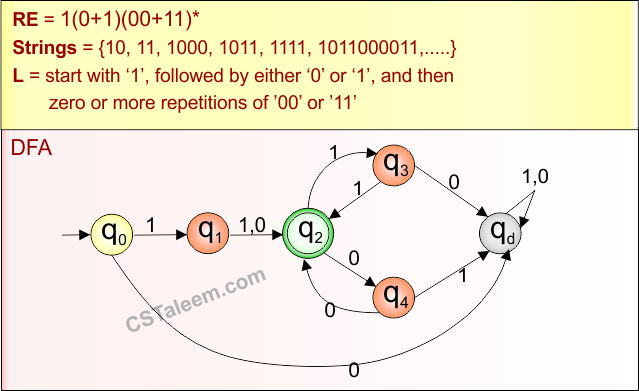
Example 2.6: Regular Expression = 1(0+1)(00+11)*
Step 01: Find the strings that can be derived from the given expression RE = 1(0+1)(00+11)*. The following figure shows all possible strings that can be derived from RE = 1(0+1)(00+11)*
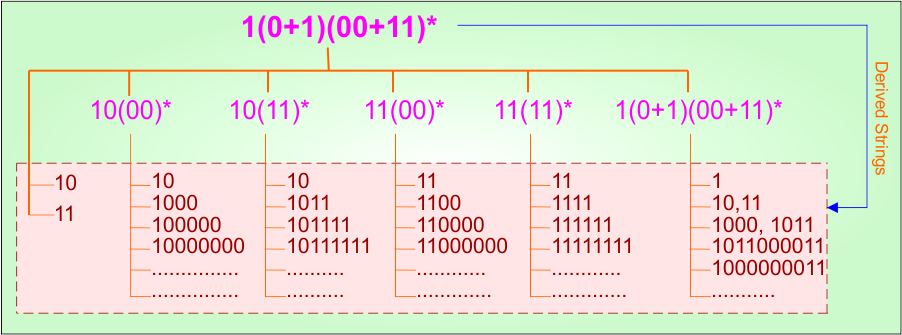
Step 02: Possible strings, Language and DFA for RE = 1(0+1)(00+11)* are given in the following diagram
Example 2.7: Regular Expression = a+b+c(ab+bb+cc)*
Step 01: Find the strings that can be derived from the given expression RE = a+b+c(ab+bb+cc)*. The following figure shows all possible strings that can be derived from RE = a+b+c(ab+bb+cc)*
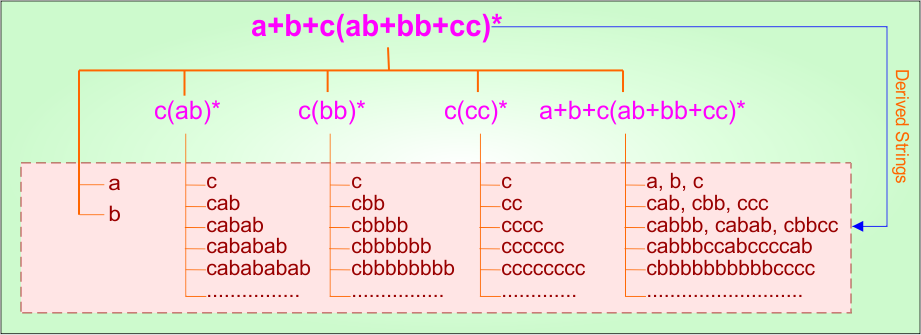
Step 02: Possible strings, Language and DFA for RE = a+b+c(ab+bb+cc)* are given in the following diagram
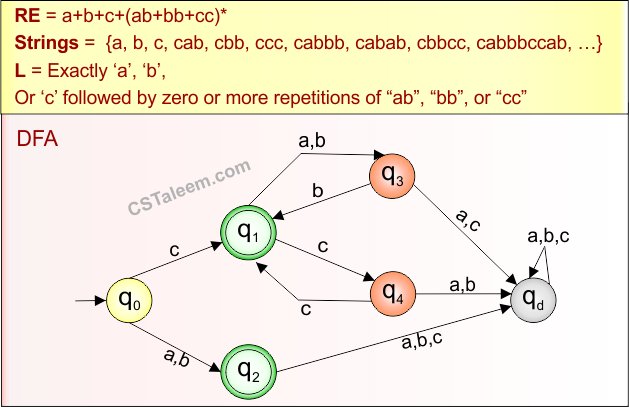
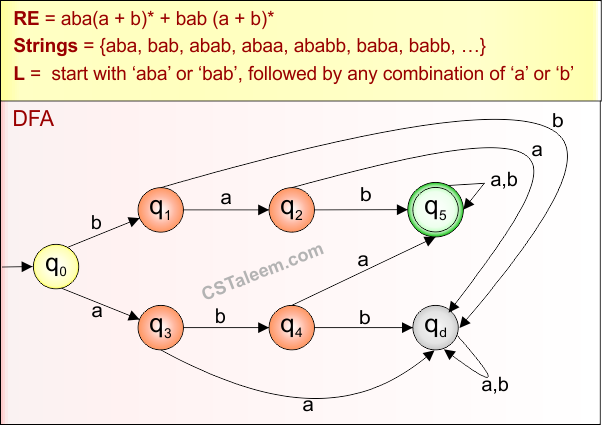
Example 2.8: Regular Expression = a+b+c+d(ab+bb+cc+dd)*
Step 01: Find the strings that can be derived from the given expression RE = a+b+c+d(ab+bb+cc+dd)*. The following figure shows all possible strings that can be derived from RE = a+b+c+d(ab+bb+cc+dd)*
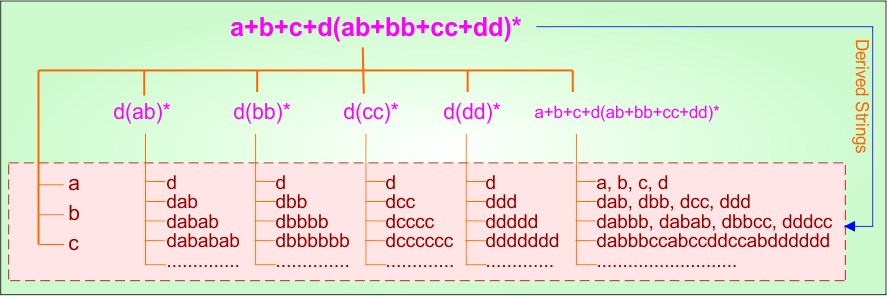
Step 02: Possible strings, Language and DFA for RE = a+b+c+d(ab+bb+cc+dd)* are given in the following diagram

Example 2.9: Regular Expression = aba(a+b)* + bab(a+b)*
Step 01: Find the strings that can be derived from the given expression RE = aba(a+b)* + bab(a+b)*. The following figure shows all possible strings that can be derived from RE = aba(a+b)* + bab(a+b)*

Step 02: Possible strings, Language, and DFA for RE = aba(a+b)* + bab(a+b)* are given in the following diagram
Category 3: End with Regular Expressions
These regular expressions describe patterns that match strings ending with specific sequences. Each one shows how a string can end after following certain rules or repetitions.
| Sr. | Regular Expression | Simple Explanation |
|---|---|---|
| 1 | (a+b+c+d)*ab |
Any mix of a, b, c, d (including empty), ending with ab. |
| 2 | (aaa+bbb)*ba |
Repeats of aaa or bbb (or none), ending with ba. |
| 3 | (a+b+c)*abc |
Any mix of a, b, or c (including empty), ending with abc. |
| 4 | (0+1)*101* |
Any mix of 0s and 1s, followed by 10, and then any number of 1’s. |
| 5 | (a+b)*a(a+b)b |
Any mix of a and b, then an aa or ab,and ending with b. |
| 6 | (00+11)*1(0+1) |
Repeats of 00 or 11 (or none), followed by 1, and then either 0 or 1. |
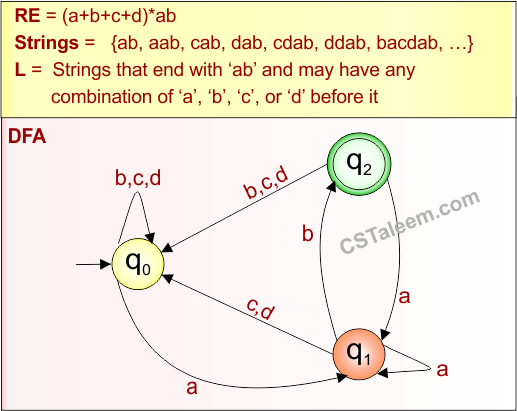
Example 3.1: Regular Expression = (a+b+c+d)*ab
Step 01: Find the strings that can be derived from the given expression RE = (a+b+c+d)*ab. The following figure shows all possible strings that can be derived from RE = (a+b+c+d)*ab
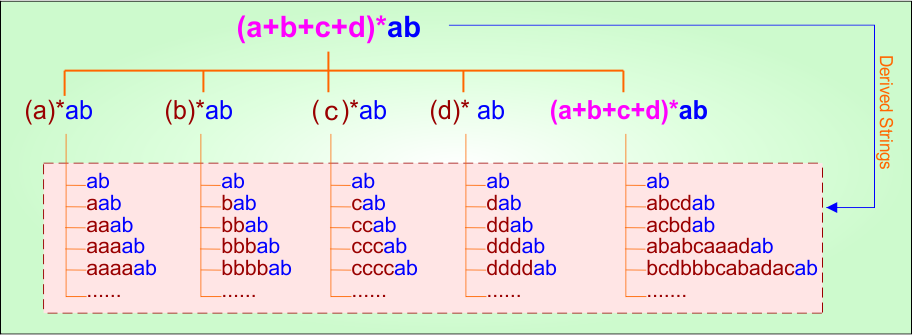
Step 02: Possible strings, Language and DFA for RE = (a+b+c+d)*ab are given in the following diagram
Example 3.2: Regular Expression = (aaa+bbb)*ba
Step 01: Find the strings that can be derived from the given expression RE = (aaa+bbb)*ba. The following figure shows all possible strings that can be derived from RE = (aaa+bbb)*ba
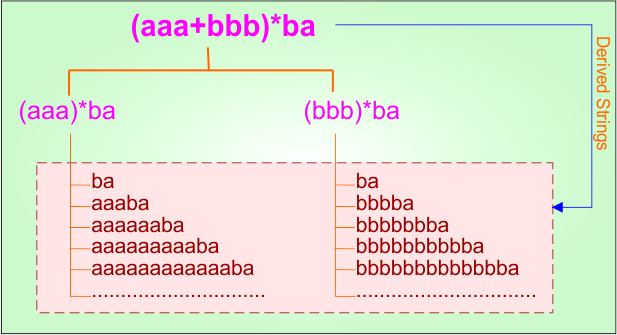
Step 02: Possible strings, Language and DFA for RE = (aaa+bbb)*ba are given in the following diagram

Example 3.3: Regular Expression = (a+b+c)*abc
Step 01: Find the strings that can be derived from the given expression RE = (a+b+c)*abc. The following figure shows all possible strings that can be derived from RE = (a+b+c)*abc
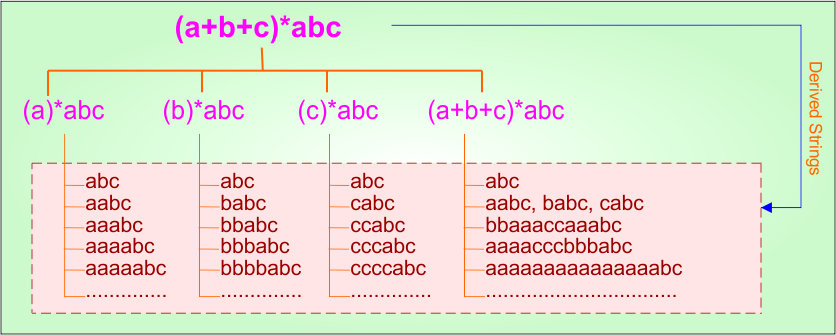
Step 02: Possible strings, Language and DFA for RE = (a+b+c)*abc are given in the following diagram
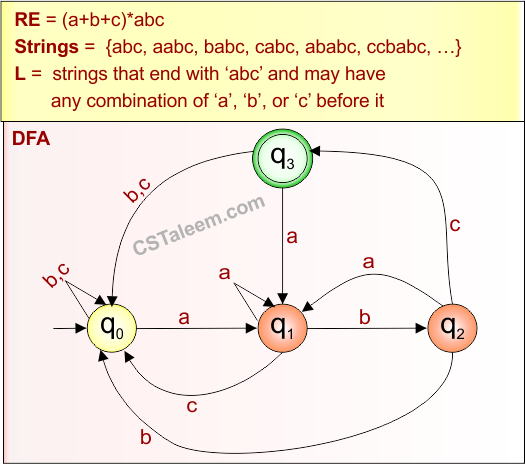
Example 3.4: Regular Expression = (0+1)*101*
Step 01: Find the strings that can be derived from the given expression RE = (0+1)*101*. The following figure shows all possible strings that can be derived from RE = (0+1)*101*
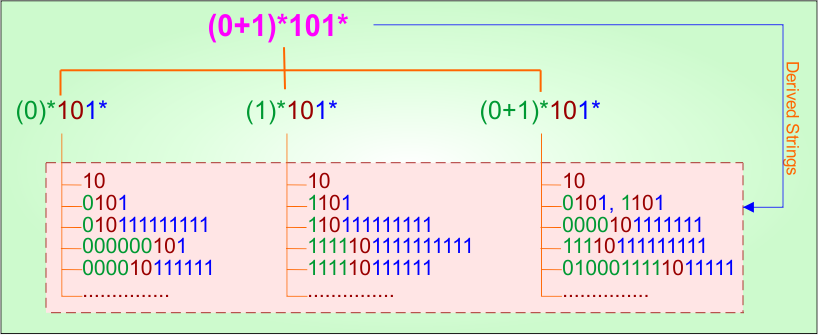
Step 02: Possible strings, Language and DFA for RE = (0+1)*101* are given in the following diagram
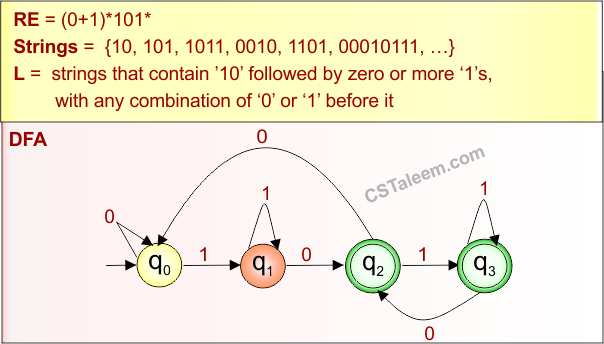
Example 3.5: Regular Expression = (a+b)*a(a+b)b
Step 01: Find the strings that can be derived from the given expression RE = (a+b)*a(a+b)b. The following figure shows all possible strings that can be derived from RE = (a+b)*a(a+b)b
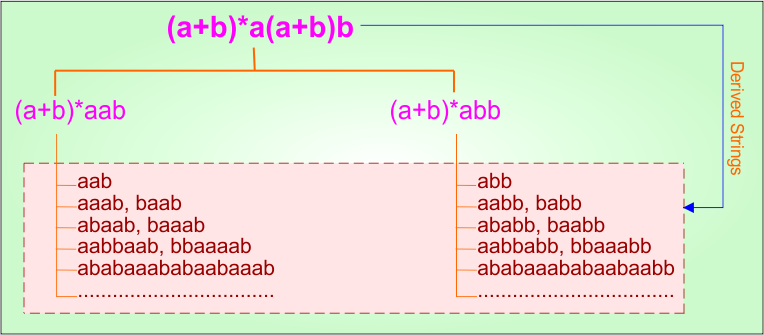
Step 02: Possible strings, Language and DFA for RE = (a+b)*a(a+b)b are given in the following diagram
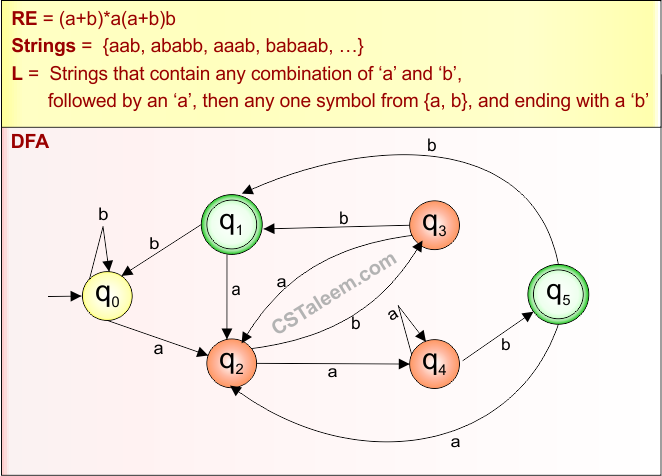
Example 3.6: Regular Expression = (00+11)*1(0+1)
Step 01: Find the strings that can be derived from the given expression RE = (00+11)*1(0+1). The following figure shows all possible strings that can be derived from RE = (00+11)*1(0+1)
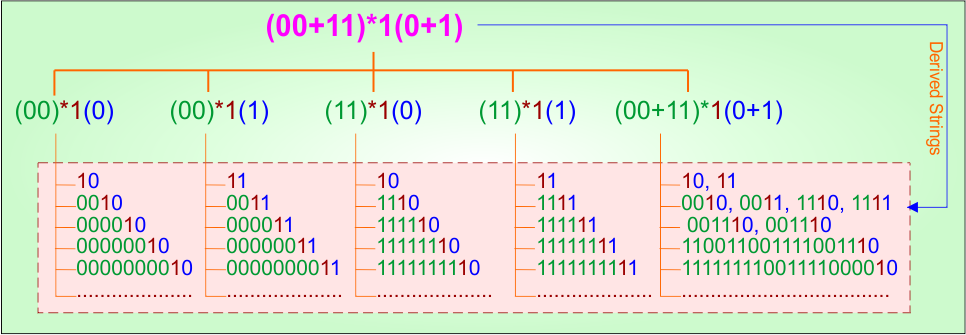
Step 02: Possible strings, Language and DFA for RE = (00+11)*1(0+1) are given in the following diagram
Category 4: Start and End with Regular Expressions
These regular expressions describe patterns that match strings that start and end with specific sequences. Each one shows how a string can start and end after following certain rules or repetitions.
| Sr. | Regular Expression | Simple Explanation |
|---|---|---|
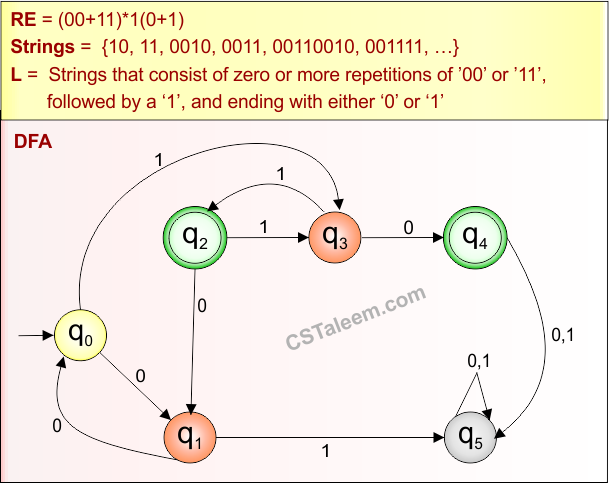
| 1 | 1(1+0)*1 + 0(1+0)*0 |
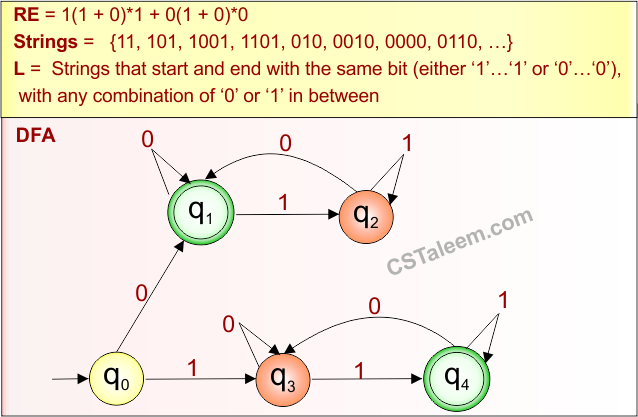
Strings that start and end with 1 or start and end with 0, and mix of 0, 1 in between |
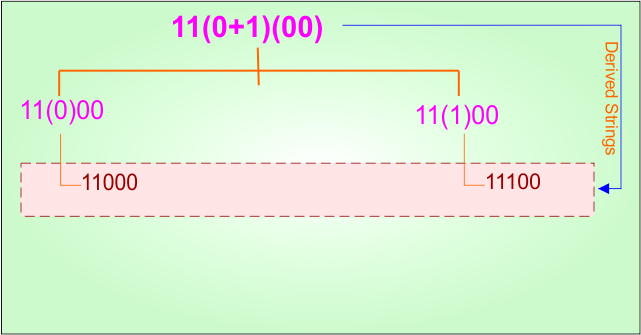
| 2 | 11(0+1)(00) |
Starts with 11, then either 0 or 1, and ends with 00. |
| 3 | 00(11)*101 |
Starts with 00, followed by any number of 11's, and ends with 101. |
| 4 | aba(aa+b)*ba |
Starts with aba, followed by any number of aa or b, and ends with ba. |
| 5 | b*(aaa+bbb)*ba |
Any number of bs, followed by any number of aaa or bbb, and ending with ba. |
| 6 | a(a+b)*ba + a |
Either just a, or starts with a, followed by any mix of as and bs, and ends with ba. |
| 7 | 0 + 1(0+1)*10 |
Either a single 0, or a string starting with 1, then anything over 0,1, and ending with 10. |
| 8 | (11)*(0+1)(00) |
Repeats of 11, followed by either 0 or 1, and ending with 00. |
| 9 | (1)*(0+1)*(00)* |
Any number of 1s, followed by any combination of 0s and 1s, followed by any number of 00s. |
| 10 | 10(101+0+1)*1 |
Starts with 10, followed by any number of 101, 0, or 1, and ends with 1. |
| 11 | ac(a+b+c)*ba |
Starts with ac, then any mix of a, b, or c, and ends with ba. |
| 12 | d(a+b+c)*bad |
Starts with d, then any mix of a, b, or c, and ends with bad. |
| 13 | acd(a+b+c)*bad |
Starts with acd, then any mix of a, b, or c, and ends with bad. |
| 14 | bb(a+b)*aa(aa+bb) |
Starts with bb, followed by any mix of as and bs, then aa, and ends with either aa or bb. |
| 15 | (aa+bb)((aa)*+b)*ba |
Starts with aa or bb, followed by any number of aas or bs, and ends with ba. |
Example 4.1: Regular Expression = 1(1+0)*1 + 0(1+0)*0
Step 01: Find the strings that can be derived from the given expression RE = 1(1+0)*1 + 0(1+0)*0. The following figure shows all possible strings that can be derived from RE = 1(1+0)*1 + 0(1+0)*0

Step 02: Possible strings, Language, and DFA for RE = 1(1+0)*1 + 0(1+0)*0 are given in the following diagram
Example 4.2: Regular Expression = 11(0+1)(00)
Step 01: Find the strings that can be derived from the given expression RE = 11(0+1)(00). The following figure shows all possible strings that can be derived from RE = 11(0+1)(00)
Step 02: Possible strings, Language, and DFA for RE = 11(0+1)(00) are given in the following diagram
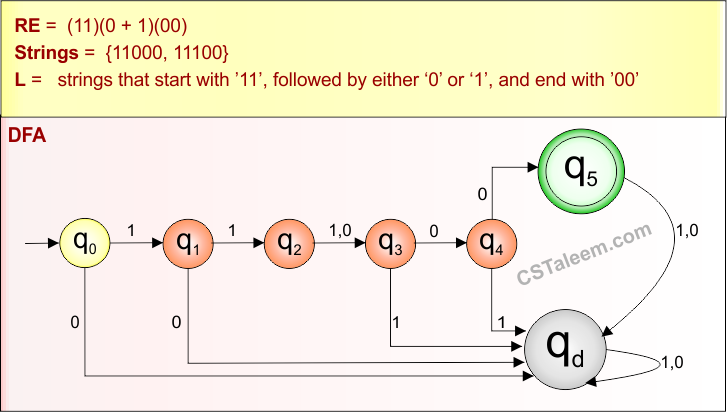
Example 4.3: Regular Expression = 00(11)*101
Step 01: Find the strings that can be derived from the given expression RE =00(11)*101. The following figure shows all possible strings that can be derived from RE =00(11)*101

Step 02: Possible strings, Language, and DFA for RE =00(11)*101 are given in the following diagram
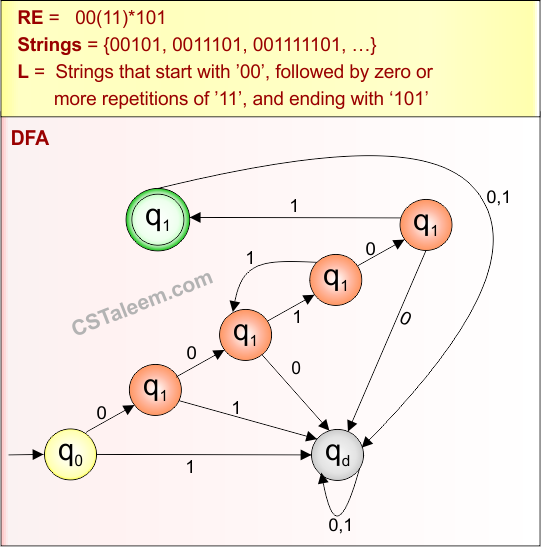
Example 4.4: Regular Expression = aba(aa+b)*ba
Step 01: Find the strings that can be derived from the given expression RE = aba(aa+b)*ba. The following figure shows all possible strings that can be derived from RE = aba(aa+b)*ba
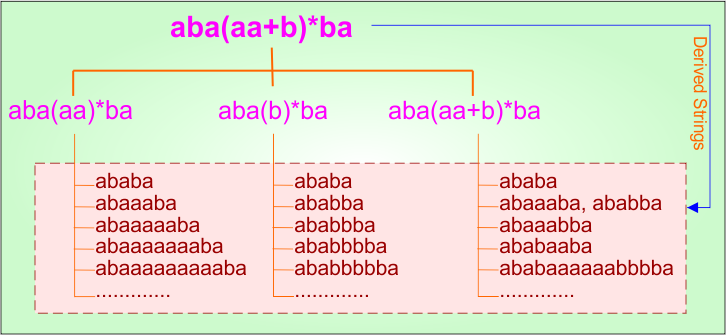
Step 02: Possible strings, Language, and DFA for RE = aba(aa+b)*ba are given in the following diagram
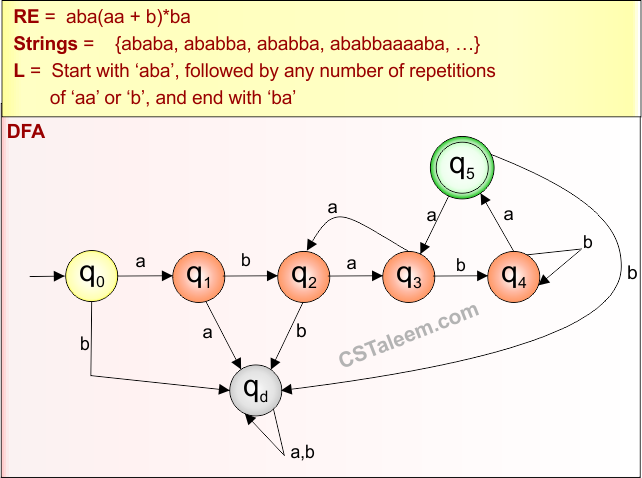
Example 4.5: Regular Expression = b*(aaa+bbb)*ba
Step 01: Find the strings that can be derived from the given expression RE = b*(aaa+bbb)*ba. The following figure shows all possible strings that can be derived from RE = b*(aaa+bbb)*ba
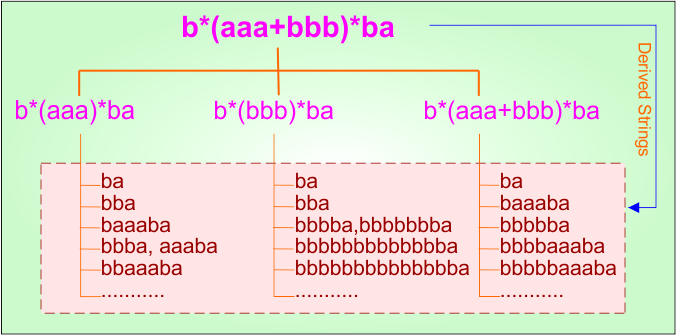
Step 02: Possible strings, Language, and DFA for RE = b*(aaa+bbb)*ba are given in the following diagram
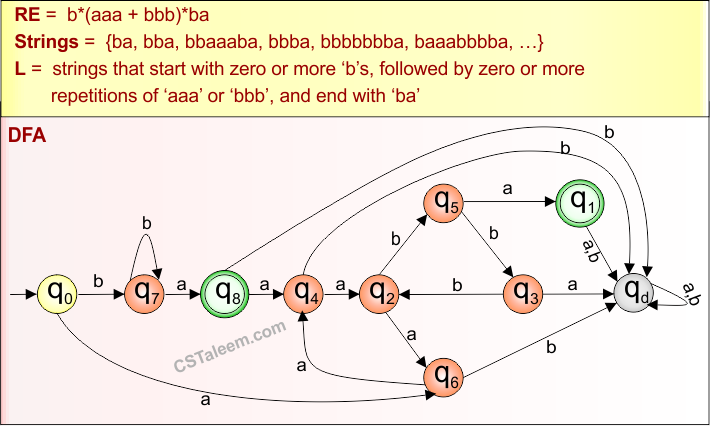
Example 4.6: Regular Expression = a(a+b)*ba+a
Step 01: Find the strings that can be derived from the given expression RE = b*(aaa+bbb)*ba. The following figure shows all possible strings that can be derived from RE = a(a+b)*ba+a
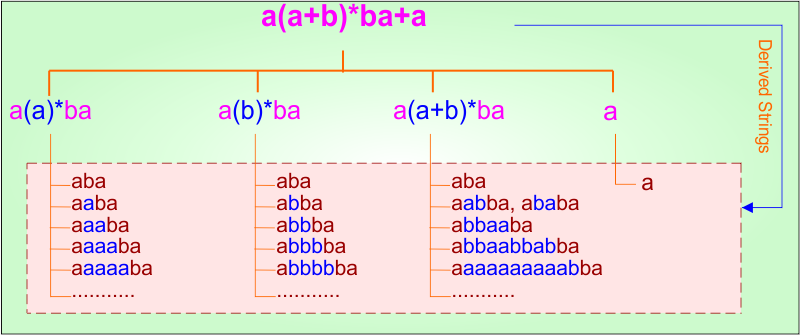
Step 02: Possible strings, Language, and DFA for RE = a(a+b)*ba+a are given in the following diagram
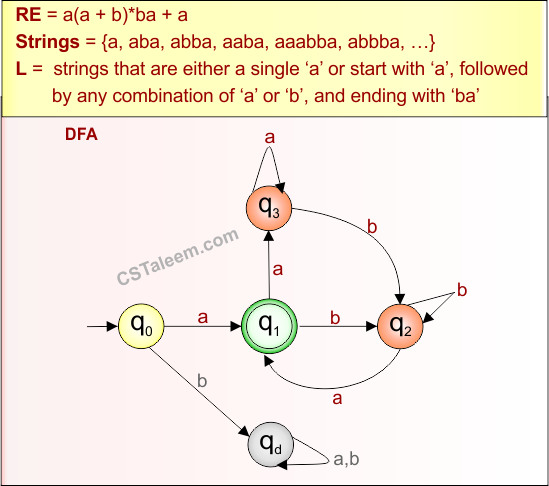
Example 4.7: Regular Expression = 0+1(0+1)*10
Step 01: Find the strings that can be derived from the given expression RE = 0+1(0+1)*10. The following figure shows all possible strings that can be derived from RE = 0+1(0+1)*10
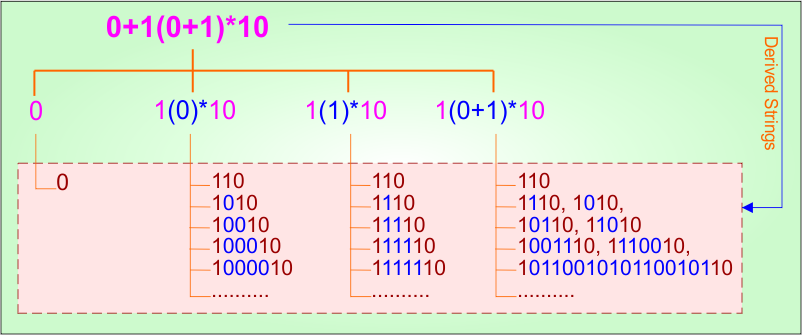
Step 02: Possible strings, Language, and DFA for RE = 0+1(0+1)*10 are given in the following diagram
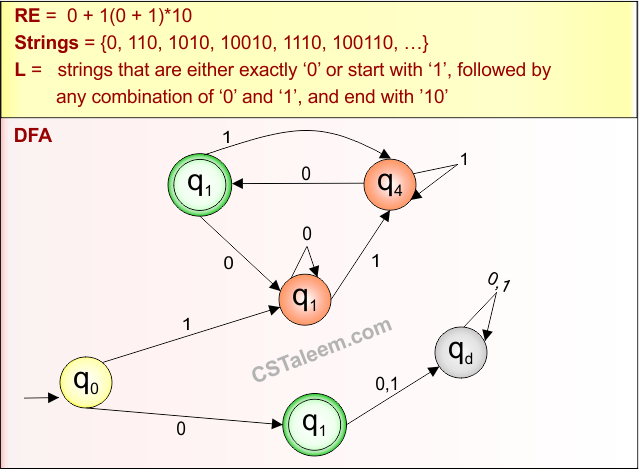
Example 4.8: Regular Expression = (11)*(0+1)(00)
Step 01: Find the strings that can be derived from the given expression RE = (11)*(0+1)(00). The following figure shows all possible strings that can be derived from RE = (11)*(0+1)(00)
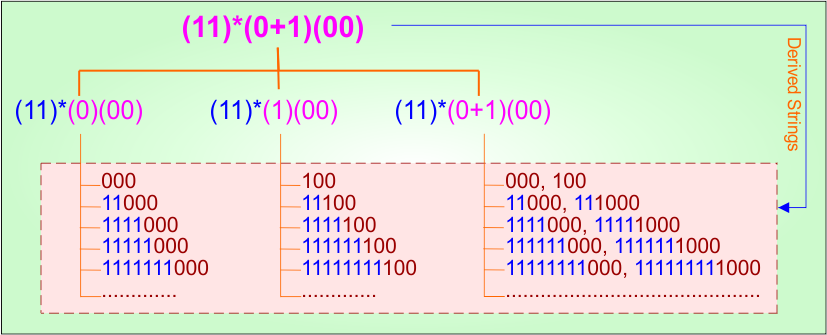
Step 02: Possible strings, Language, and DFA for RE = (11)*(0+1)(00) are given in the following diagram
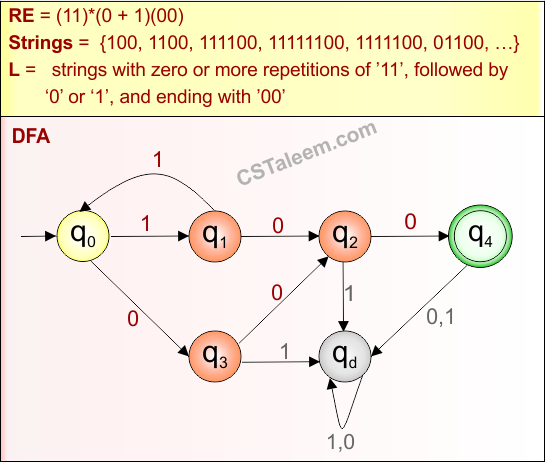
Example 4.9: Regular Expression = (1)*(0+1)*(00)*
Step 01: Find the strings that can be derived from the given expression RE = (1)*(0+1)*(00)*. The following figure shows all possible strings that can be derived from RE = (1)*(0+1)*(00)*
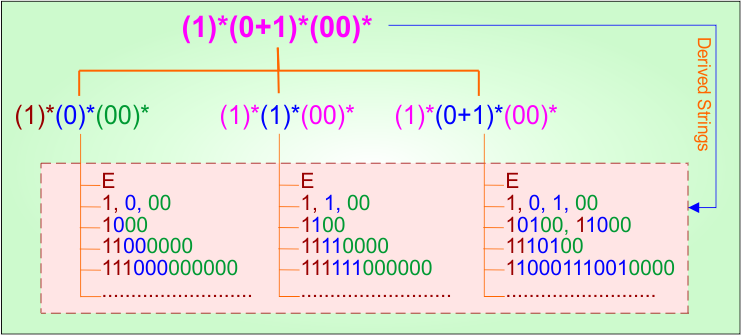
Step 02: Possible strings, Language, and DFA for RE = (1)*(0+1)*(00)* are given in the following diagram
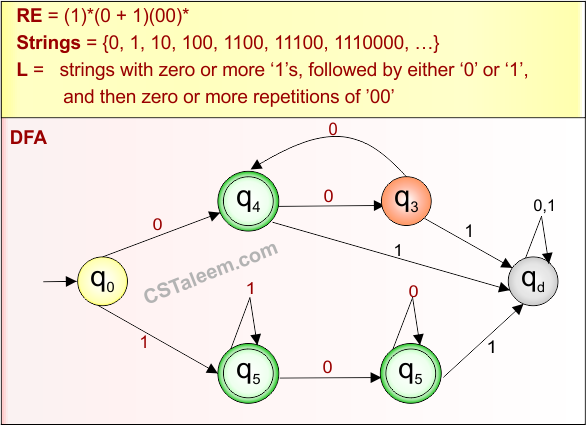
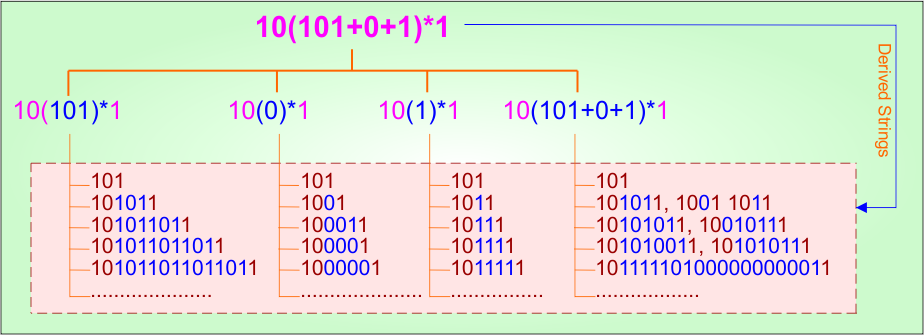
Example 4.10: Regular Expression = 10(101+0+1)*1
Step 01: Find the strings that can be derived from the given expression RE = 10(101+0+1)*1. The following figure shows all possible strings that can be derived from RE = 10(101+0+1)*1
Step 02: Possible strings, Language, and DFA for RE = 10(101+0+1)*1 are given in the following diagram
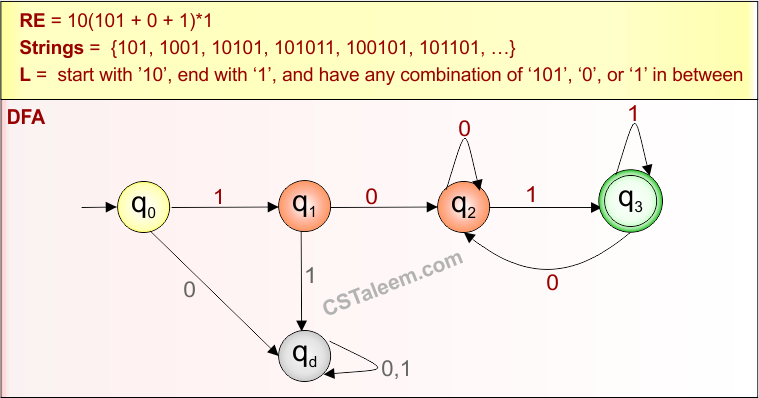
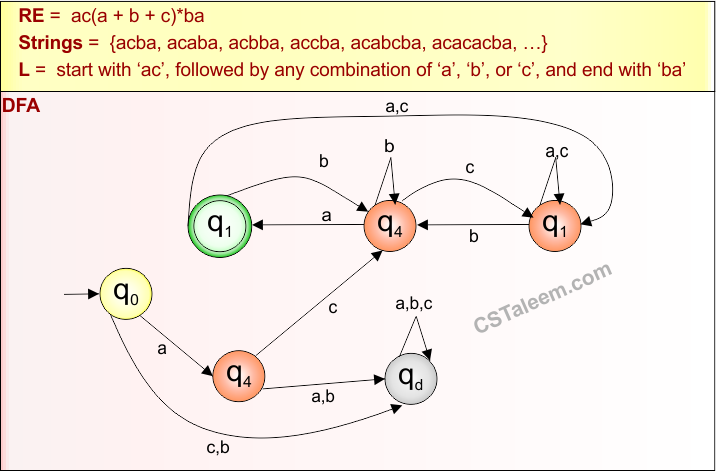
Example 4.11: Regular Expression = ac(a+b+c)*ba
Step 01: Find the strings that can be derived from the given expression RE = ac(a+b+c)*ba. The following figure shows all possible strings that can be derived from RE = ac(a+b+c)*ba
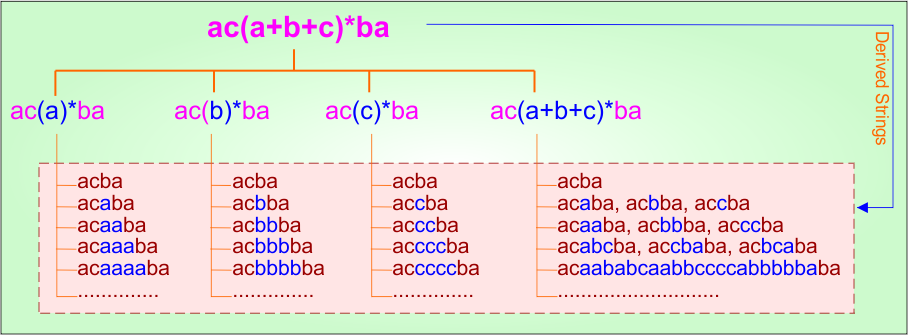
Step 02: Possible strings, Language, and DFA for RE = ac(a+b+c)*ba are given in the following diagram
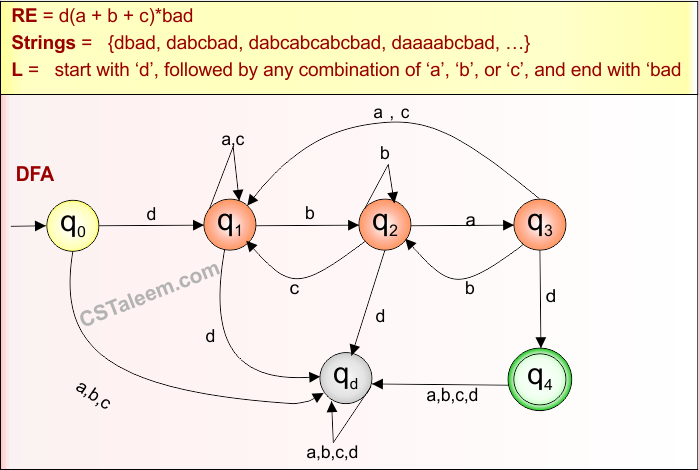
Example 4.12: Regular Expression = d(a+b+c)*bad
Step 01: Find the strings that can be derived from the given expression RE = d(a+b+c)*bad. The following figure shows all possible strings that can be derived from RE = d(a+b+c)*bad
Step 02: Possible strings, Language, and DFA for RE = d(a+b+c)*bad are given in the following diagram
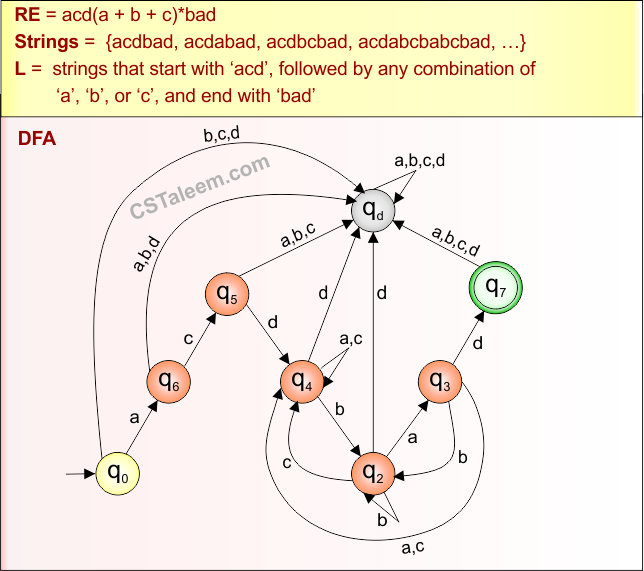
Example 4.13: Regular Expression = acd(a+b+c)*bad
Step 01: Find the strings that can be derived from the given expression RE = acd(a+b+c)*bad . The following figure shows all possible strings that can be derived from RE = acd(a+b+c)*bad 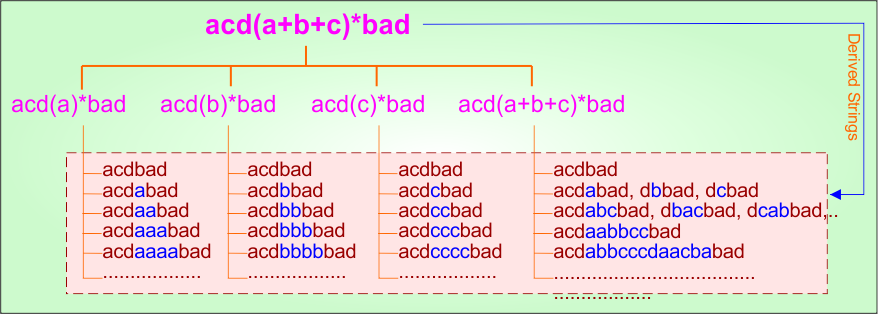
Step 02: Possible strings, Language, and DFA for RE = acd(a+b+c)*bad are given in the following diagram
Example 4.14: Regular Expression = bb(a+b)*aa(aa+bb)
Step 01: Find the strings that can be derived from the given expression RE = bb(a+b)*aa(aa+bb). The following figure shows all possible strings that can be derived from RE = bb(a+b)*aa(aa+bb)
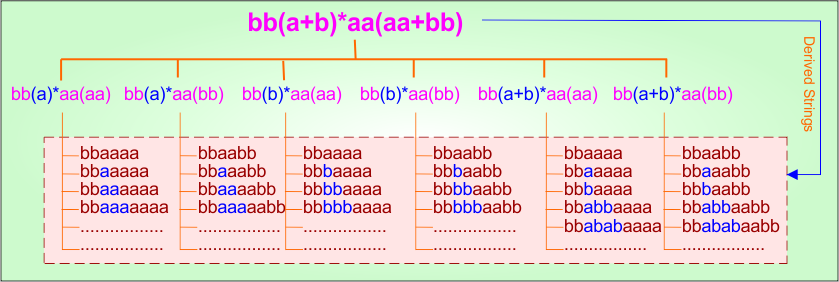
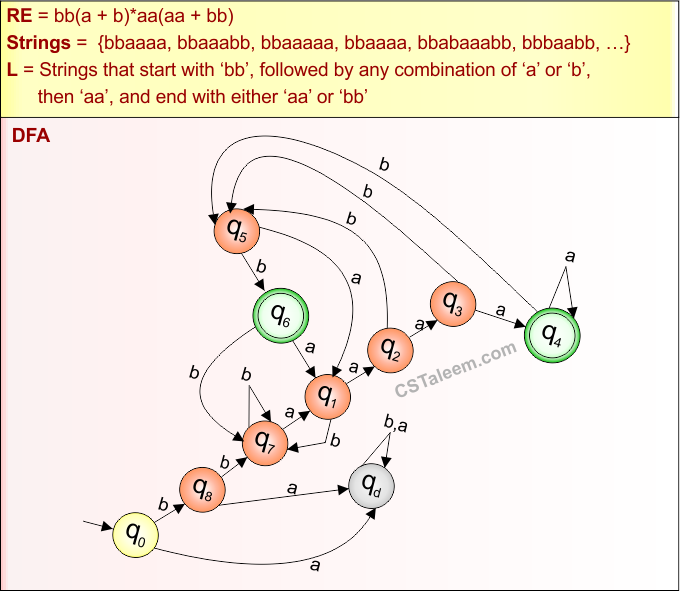
Step 02: Possible strings, Language, and DFA for RE = bb(a+b)*aa(aa+bb) are given in the following diagram
Example 4.15: Regular Expression = (aa+bb)((aa)*+b)*ba
Step 01: Find the strings that can be derived from the given expression RE = (aa+bb)((aa)*+b)*ba. The following figure shows all possible strings that can be derived from RE = (aa+bb)((aa)*+b)*ba
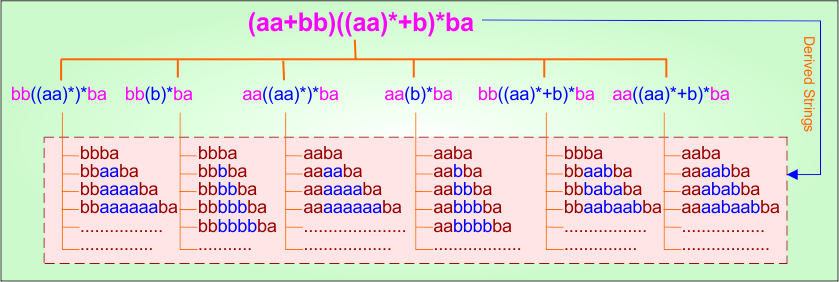
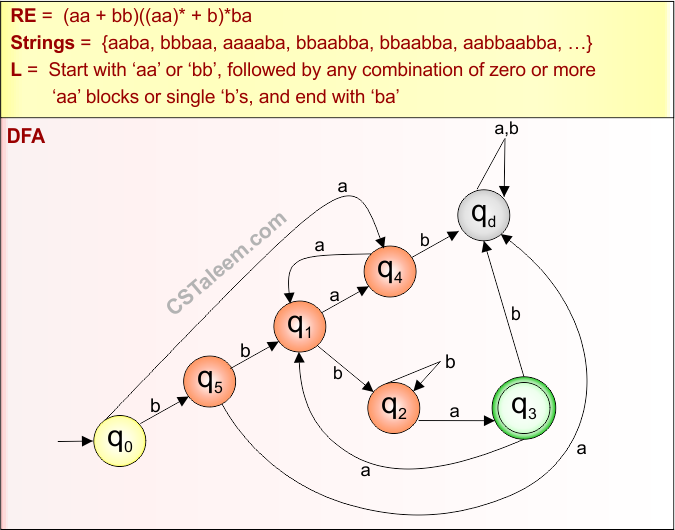
Step 02: Possible strings, Language, and DFA for RE = (aa+bb)((aa)*+b)*ba are given in the following diagram
Types of Regular Expressions in TOC
As we know, regular languages are either finite or infinite. So, Regular expressions can be written for both finite and infinite languages. So, types of Regular expressions are of two types
I. Finite Regular Expressions
Finite Regular expressions are used to represent the finite regular languages. So, the length of finite regular expressions is always limited. Following are the various examples of finite regular expressions
Example 01: Write the regular expression for the language which has no string.
Solution: Language for the given example is given below
L = { } //empty string
Regular expression for the above language is given below
L(R) = Φ
Example 02: Write the regular expression for the language with a string with zero length.
Solution: Language for the given example is given below
L = { ε } //single string
Regular expression for the above language is given below
L(R) = ε
Example 03: Write the regular expression for the language with a string with a single length over ∑ = {a, b}.
Solution: Language for the given example is given below
L = { a,b } //string with single length
A regular expression for the above language is given below
L(R) = (a+b)
Example 04: Write the regular expression for the language with a string with the length of two over ∑ = {a, b}.
Solution: Language for the given example is given below
L = (a,b).(a,b) = { aa,ab,ba,bb } //string with length of two
A regular expression for the above language is given below
L(R) = (aa+ab+ba+bb)
Example 05: Write the regular expression for the language with a string of three over ∑ = {a, b}.
Solution: Language for the given example is given below
L = (a,b).(a,b). (a,b) = { aaa,abb,aab,baa……..,bbb } //string with length of three
Regular expression for the above language is given below
L(R) = (aaa + abb + aab + baa+……..+ bbb)
Example 06: Write the regular expression for the language with strings with an at-most length of 2 over ∑ = {a, b}.
Solution: Language for the given example is given below
L = (ε,a,b).( ε,a,b) = { ε, a ,b, aa,ba……..,bb } // strings with at-most length of 2
Regular expression for the above language is given below
L(R) = (ε+a+b).( ε+a+b)
Example 07: Write the regular expression for the language with strings “Not More than two a’s and one b” over ∑ = {a, b}.
Solution: Language for the given example is given below
L = { ε, a ,b, aa,aba, aab…….. } // strings with Not More than two a’s and one b
Regular expression for the above language is given below
L(R) = { ε + a + b + aa +aba + aab+…….. }
Example 08: Write the regular expression for the finite language, which accepts all the strings, having the length exactly two over ∑ = {a, b}.
Solution: Language for the given example is given below
L = {aa, ab, ba, bb} // only 4 strings are possible for given condition
Regular expression for the above language is given below
L(R) = {aa + ab +ba+bb}
II. Infinite Regular Expressions
Infinite regular expressions are used to represent the infinite regular languages. So, the length of infinite regular expressions is always unlimited. Let explain various examples
Example 01: Write the regular expression for the language that accepts all the strings having all combinations of a’s over ∑ = {a}.
Solution: Language for the given example is given below
L = { ε, a, aa, aaa, aaaa, aaaaa, ……….. }
A regular expression for the above language is given below
L(R) = a*
Example 02: Write the regular expression for the language that accepts all the strings having all combinations of a’s except the null string over ∑ = {a}.
Solution: Language for the given example is given below
L = {a, aa, aaa, aaaa, aaaaa, ……….. }
A regular expression for the above language is given below
L(R) = a+
Example 03: Write the regular expression for the language that accepts all the strings, which has any number of a’s and b’s over ∑ = {a, b}.
Solution: Language for the given example is given below
L = {a, b, ab, ba, aab, aba, aaba ……….. }
Regular expression for the above language is given below
L(R) = (a+b)*
Example 04: Write the regular expression for the language that accepts all the strings, having only one “b” and any numbers of “a” over ∑ = {a, b}.
Solution: Language for the given example is given below
L = {b, ab, aba, abaa, abaaaa, aaaaabaaaaaaa……….. } // all strings having only one “b”
Regular expression for the above language is given below
L(R) = a*ba*
Example 05: Write the regular expression for the language that accepts all the strings, which are starting with 1 and ending with 0, over ∑ = {0, 1}.
Solution: The language for the given example is given below
L = {10, 100, 11010, 1110, 1111000, ……….. } // starting with 1 and ending with 0
Regular expression for the above language is given below
L(R) = 1(0+1)*0
Example 06: Write the regular expression for the language that accepts all the strings having even length, over ∑ = {0}.
Solution: Language for the given example is given below
L = { ε, 00, 0000, 000000, 00000000, ……….. }
Regular expression for the above language is given below
L(R) = (00)*
Example 07:Write the regular expression for the language which accepts all the strings, having the first symbol should be “b” and the last symbol should be “a” over ∑ = {a, b}.
Solution: Language for given example is given below
L = {ba, baa, baba, bbaa, baaaa, babbbba……….. } // unlimited strings are possible for given condition
Regular expression for above language is given below
L(R) = b (a+b)* a
Operations on Regular Languages in Automata
There may be various operations in regular languages. Let “R” be a Regular expression over the alphabet Sigma if R is
1. If regular expression (R) is equal to Epsilon (ε), then the language of Regular expression (R) will represent the epsilon set, i.e. { ε}. A mathematical equation is given below,
![]()
2. If regular expression (R) is equal to Φ, then the language of Regular expression (R) will represent the empty set, i.e. { }. The mathematical equation is given below,
![]()
3. If regular expression (R) is equal to an input symbol “a,” which belongs to sigma, then the language of Regular expression (R) will represent the set which has “a” alphabet, i.e. {a}. A mathematical equation is given below,
![]()
4. The union of two Two Regular Expressions will always produce a regular language. Suppose R1 and R2 are two regular expressions. IF R1= a, R2=b then R1 U R2 =a+b So L(R1 U R2) = {a,b}, still string “a,b” is a regular language.

Hence, the above equation shows that {a,b} is also a regular language.
Note: The intersection of two Two Regular Expressions will always produce a regular language.
5. Concatenation of two Two Regular Expressions will always produce a regular language. IF R1= a, R2=b then R1.R2 =a.b So L(R1.R2) = {ab}, still string “ab” is a regular language

Hence, the above equation shows {ab} is also a regular language.
6. Kleene closure of Regular Expression (RE) is also a regular language
If R1 = x and (R1)* is still a regular language
- In a regular expression, x* means zero or more occurrences of x. It can generate { ε, x, xx, xxx, xxxx, …..}
- In a regular expression, x+means one or more occurrence of x. It can generate {x, xx, xxx, xxxx, …..}
7. If R is regular, (R) is also a regular language
Note: Only the above mentioned 7 rules are used for regular expressions. By the combination of above 7-rules more regular Expressions can be created.














