PDA in TOC
A pushdown automaton (PDA) is a way to implement a context-free grammar (CFG) in a similar way we design Finite Automata (FA) for a regular grammar (RG) in TOC. A DFA has limited memory, but a PDA can hold unlimited memory.
Basically, a Pushdown Automaton is
“Finite Automata Machine” + “a stack”, where
- FA represents a finite memory for a finite number of states
- A stack is an extra memory with infinite size to PUSH and POP values.
Basic Operation of PDA in TOC
PUSH and POP are two basic Operations in PDA which are always performed on the top of the stack in TOC. The following diagram shows it simply how PUSH and POP works with stack

NO-Operation (Ignore) Operation in PDAIn PDA operations, NO-OP (or “Ignore”) means that the stack remains unchanged during a particular transition. That is:
|
Components of PDA in TOC
A pushdown automaton has 3 basic components in TOC
- Input tape: It contains the input string.
- Control unit: It takes an input and forwards it to the stack for PUSH or POP.
- Stack: It is the memory of infinite size.
The following diagram explains the above components.
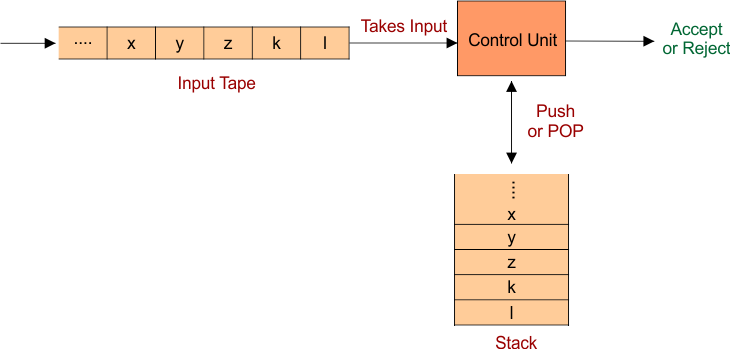
Note: A PDA may or may not PUSH or POP an input symbol in every transition. But PDA has to read the top of the stack in every transition.
7-Tuples of Pushdown Automata (PDA)
Pushdown Automata (PDA) can be formally described by 7-tuples (Q, ∑, Γ, δ, q0, Z0, F)
- Qis, the finite number of states,
- ∑ is the input alphabet, which is PUSH or POP from Stack.
- Γ is a stack of symbols.
- Transition function: Q × (∑ ∪ {ε}) x Γ → Q × Γ *
- q0 is the start state (q0 ∈ Q)
- Z0 is the default value of the stack. It is used to represent the Null value of the stack. We can say Z0 is an epsilon.
- F is a set of Final states (F ∈ Q). Final states may or may not exist in PDA.
Trnsition function Notations:
|
PDA Transition Function in TOC
In TOC, the term “transition” refers to the change of state (including staying in the same state, i.e., a self-loop) in a machine when it reads an input symbol (including epsilon).
The transition function can perform any operation (PUSH, POP, No OP) by using the following input
- Current state
- Input symbol
- Top of Stack Symbol

In PDA, the transitions function requied when we want to perform any of the following operation.
- PUSH Operation
- POP Operation
- No Operation
Let’s explain all three operations
1. PUSH Operation
It adds symbols at the top of the stack. The transition function for the PUSH operation is given below
δ(Q,a,X)=(Q’,Y), where Y≠ε, Y≠X
Following diagram explain the working of PUSH operation in PDA in detail

Working of the PUSH Transition Function is given below
-
Read any input symbol, i.e., (
aor ε) -
Check conditions for the PUSH operation. If the stack top is
X which should not equal to Y (i.e. Y≠X) and Y is also not equal to an epsilon (i.e. Y≠ε) then, first POP X from stack, append Y with X, PUSH XY into stack, where Y remains at top of stack. -
Result: Stack grows as it adds new symbols (i.e., 0)
-
Example:
-
δ(q0,0,Z0)=(q0,0Z0)
-
In this example, the stack top “Z0“ is replaced with “0Z0“, where “0” is now at the top of the stack.
2. POP Operation
It removes symbols at the top of the stack. The transition function for the POP operation is given below
δ(Q,a,X)=(Q’,Y), where Y = ε
Following diagram explain the working of POP operation in PDA in detail
Working of the POP Transition Function is given below
-
Read any input symbol, i.e., (
aor ε) -
Check conditions for the POP operation. If
Y is equal to an epsilon (i.e. Y= ε) then, POP the stack top element and push nothing -
Result: Stack size decreases by 1 as it remove a symbols (i.e., 0)
-
Example:
-
δ(q0,0,0)=(q0,
ε)
-
In this example, the stack top “0“ is removed from the top of the stack.
3. No Operation
It is a special case where stack remains unchanged. The transition function for the No operation is given below
δ(Q,a,X)=(Q’,Y), where Y = X
Following diagram explain the working of No operation in PDA in detail
Working of the No Operation Transition Function is given below
-
Read any input symbol, i.e., (
aor ε) -
Check conditions for the No operation. If
Y is equal to X then, stack remains unchanged -
Result: It first remove the top element (“X”) and PUSH back again (“X”) at the top of stack in PDA. So stack remains unchanged
-
Example:
-
δ(q0,0,0)=(q0,0)
-
In this example, the stack top “0“ is POP first and instantly PUSH back to stack.
By default value of stack is mostly consider Z0. When we fount only Z0 in stack, it considered empty stack.
Transition Function in the State Diagram of PDA
We use the short form of transition function in state diagrams of pushdown automata. Here is the short form of PDA transition function.
- Transition function Full Form : δ(Q,a,X)=(Q’,Y)
- Transition function Short Form : (a , X / Y)

General Representation of Transition Function
Let us see the following diagram, which shows a general representation of transition in a PDA from a state q0 to state q1, labeled as x,y → z

This means at state q0, if we consume an input string ‘x’ and the top symbol of the stack is ‘y’, then we push ‘z’ on top of the stack and move to the next state q1...
Example of PDA in TOC
Let suppose a Language A = 0n1n where n ≥ 1
- Accepted Strings Examples: 01, 0011, 000111, 00001111, ……….
- Rejected Strings Examples: 0,1, 10, 1100, 0101, 1001, ………
The behaviour of PDA with stack and input tap, before and after transition, is given below in various steps
Consider a string "0011" and check how it is accepted by the PDA.
Step 01: PUSH “0” into the stack
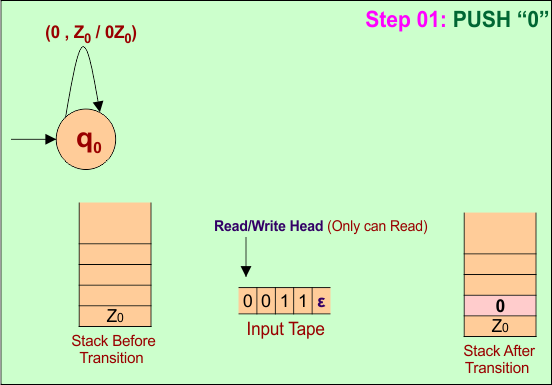
Step 02: PUSH the second “0” into the stack

Step 03: POP “0” from the stack

Step 04: POP the second “0” from the stack

Step 05: Finally, the stack is empty, and string (“0011”) from language (0n1n where n≥1) is accepted

Types of PDA
There are two main types of Pushdown Automata, one is DPDA andthe other is NPDA
-
Deterministic Pushdown Automata (DPDA): At any point, the machine has at most one possible move; no ambiguity in state transitions.
-
Non-deterministic Pushdown Automata (NPDA): The machine may have multiple possible moves from a given configuration, allowing branching paths.
Let’s explain a bit in detail
1. Deterministic Pushdown Automaton (DPDA)
For every combination of state, input symbol, and top of stack, there is at most one possible move. DPDA is less powerful than NPDA (cannot accept all context-free languages). It is used in deterministic parsing (e.g., in compilers for programming languages).
2. Nondeterministic Pushdown Automaton (NPDA)
It can have multiple possible moves for the same input and stack condition. NPDA is More powerful than DPDA (can accept all context-free languages). Typically used in theoretical models and language recognition.
Note: For some contex free languages, we can construct DPDA and NPDA. But there are some languages which are only accepted by NPDA but are not by DPDA. That’s why we consider NPDA is more powerfull than DPDA.
Memory Models in PDAs
There are two basic memory models used in PDA.
- Single-stack PDA
- Double Stack PDA
Important: more than 2 stacks can be added to a PDA, but they do not increase its computational power beyond what is achievable with just 2 stacks (which equals the power of a Turing Machine).
1. Single-Stack PDA (1-Stack PDA)
- It uses one stack as memory.
- Can recognize Context-Free Languages (CFLs).
- Operates by pushing and popping symbols on the stack based on input symbols and current states.
- Example language:
{ aⁿ bⁿ | n ≥ 0 }, where the number ofas equals the number ofbs. - Limitation: Cannot recognize languages that require comparing three types of symbols, such as
{ aⁿ bⁿ cⁿ }. - This model corresponds exactly to non-deterministic context-free grammars.
2. Double-Stack PDA (2-Stack PDA)
- Uses two independent stacks for memory.
- Has the same computational power as a Turing Machine.
- Can recognize Recursively Enumerable Languages, which includes context-sensitive and some non-context-free languages.
- Example language:
{ aⁿ bⁿ cⁿ | n ≥ 0 }, which requires comparing three types of symbols. - The two stacks together can simulate the read/write tape of a Turing machine, making the model computationally complete.
We conclude that single stack to a double stack enhances the computational power of a PDA. 1-stack PDA is limited to context-free languages, while a 2-stack PDA computional power is equivalent to Turing machine and thus recognize a much broader class of languages.
Applications of PDA
PDAs are used in various practical and theoretical applications, mainly involving context-free languages.
1. Syntax Analysis / Parsing
Used in compilers for checking the syntax of programming languages (e.g., using LL or LR parsers).
2. Language Recognition
PDAs can recognize context-free languages (CFLs) such as:
-
Balanced parentheses:
( ( ) ) -
Palindromes (e.g.,
abba) -
Arithmetic expressions with nested structure
3. Natural Language Processing
-
Some aspects of natural language grammars can be modeled using context-free grammars and PDAs.
4. XML/HTML Parsing
-
Validating proper nesting of tags (e.g.,
<html><body></body></html>) mimics PDA behavior.
Comparison: PDA vs FA vs TM
| Feature | Finite Automata (FA) | Pushdown Automata (PDA) | Turing Machine (TM) |
|---|---|---|---|
| Memory | No memory (only states) | Stack (LIFO memory) | Infinite tape (full memory) |
| Input Language | Regular languages | Context-free languages | Recursively enumerable languages |
| Power | Least powerful | More powerful than FA | Most powerful |
| Stack/Tape | None | Stack | Infinite tape (read/write) |
| Backtracking/Nondeterminism | NFA allowed | NPDA common | Nondeterministic TM |
| Acceptance | Final state | Final state or empty stack | Final state or halting |
| Used In | Simple pattern matching (e.g., regex) | Parsing (e.g., programming languages) | General computation (e.g., simulating algorithms) |
















