Turing Machine in TOC
The Turing Machine is a mathematical computation model that accepts Recursive Enumerable Languages (ERL) in TOC (Theory of Computation). The mathematician and logician Alan Turing invented the Turing machine in 1936. Turing machine is not a physical device but a theoretical model for some computations.
A Turing Machine can accept a wide range of languages, including:
- Regular Languages (RL)
- Context-Free Languages (CFL)
- Context-Sensitive Languages (CSL)
- Recursively Enumerable Languages (RL)
It can also accept all recursive languages, which are a subset of recursively enumerable languages. Turing Machines are extremely powerful and can recognize languages that simpler machines like Finite Automata (FA) and Pushdown Automata (PDA) cannot, giving them the ability to accept a wide variety of language classes.
Elements of a Turing Machine
The turning machine has the essential elements given below.
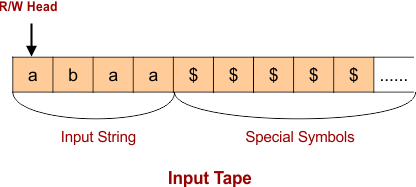
1. Input Tape: It has an infinite length for performing read and write operations.
2. Input Symbols: The input tape consists of infinite cells, each containing either an input or a special symbol. A special symbol is also called a blank symbol in an automata, the Turing machine.
- Input Symbols (∑) an be in the form of {0,1, a, b, ε, Z0}
- Special Symbols (B) can be in the form of {&, $,],[, #, etc. }
3. Head pointer: A read/write head pointer that points to the cell being read/write and can move in both (left and right) directions.
Following is a descriptive diagram of the Turing Machine.
4. A State Register: This holds the state of the machine at any point.
Operation on Input Tape in Turing Machine
Let’s explain the basic operations over Input Tape.
- Read/scan the symbol below the tap Head
- Update / Write a symbol below the Tap Head
- Move the Tap Head one step LEFT or RIGHT
Let’s see the descriptive diagram
Important:
|
Computation Result in Turing Machine
The following are all possible results after performing all operations on the input tape.
- HALT and ACCEPT: We reach an accepted state when we have done all operations.
- HALT and REJECT: We get a rejected state after doing all operations.
- LOOP: it means the machine fails to HALT or reject
Note: HALT is also called STOP
Types of Turing Machines
Here are several types of Turing machines
1. Multi-tape Turing Machine
A multi-tape Turing machine is an extension of the standard Turing machine that uses multiple tapes for input, output, and computation. Each tape has its own read-write head, and the machine’s operation depends on the symbols read from each tape.
Example: To check if a binary string is a palindrome, a two-tape machine works as follows:
- Copy Input: The machine copies the string from the first tape to the second.
- Compare: It compares symbols by reading the first tape left to right and the second tape right to left.
- Efficiency: If all symbols match, the string is a palindrome. This process is faster than using a single-tape machine, reducing time complexity.
2. Multi-head Turing Machine
A multi-head Turing machine is an extension of the standard Turing machine that uses multiple read-write heads on a single tape. Each head moves independently, reading and writing symbols on the same tape.
Example: To check if a binary string is a palindrome, a multi-head Turing machine works as follows:
- Initialize Heads: One head starts at the leftmost symbol, and the other starts at the rightmost symbol of the string.
- Compare: The heads move towards each other, comparing the corresponding symbols on the tape.
- Efficiency: If all symbols match as the heads meet, the string is a palindrome. This process is faster than using a single head, as both sides of the string are checked simultaneously, reducing time complexity.
3. Multi-tape Multi-head Turing Machine:
The multi-tape multi-head Turing machine has several tapes, each controlled by its own head. A multi-tape multi-head Turing machine can be simulated by a standard Turing machine.
4. Two-Way Infinite Tape Turing Machine
A Two-Way Infinite Tape Turing Machine is an extension of the standard Turing machine where the tape extends infinitely in both directions. This means that the machine’s read-write head can move freely in both left and right directions, providing more flexibility and efficiency in computation.
5. K-Dimensional Turing Machine
A K-dimensional Turing machine extends the concept of a standard Turing machine by allowing the tape to exist in multiple dimensions. The read-write head can move left, right, up, and down, giving it more flexibility compared to a standard Turing machine that only moves left and right on a one-dimensional tape.
For example, a two-dimensional Turing machine has a tape that extends infinitely in both the X and Y directions, like a grid. This extra flexibility makes a K-dimensional Turing machine suitable for tasks that involve multi-dimensional data, such as:
- Image processing
- Simulations of physical phenomena
- Handling matrices or grids
In simple terms, a K-dimensional Turing machine can handle more complex data by working in multiple directions, making it ideal for tasks involving 2D or higher-dimensional spaces.
6. Non-Deterministic Turing Machine (NDTM)
A non-deterministic Turing machine (NDTM) is different from a regular deterministic Turing machine (DTM) because it can move to multiple possible states from a given state and symbol. Instead of following just one path, the NDTM can explore many paths at once.
Turing Machine 7 Tuples
let’s see the 7-tuples (Q, T, B, ∑, δ, q0, F) which show the mechanism of the Turning machine. Following are the 7-Tuples of the Turing machine.
- Q contains a finite set of states.
- T is the input tape that holds the Input and Special symbols. So, Both input and Special symbols are subsets of input tape T.
- B is a Special symbol, also called a Blank symbol (every cell is filled with a special symbol except the input alphabet initially)
- ∑ is the input symbols (input tape holds initial input alphabet)
- δ is a transition function is Q × T → Q × T × {L,R}. At any state (Q) when the
- If the input tape symbol (T) is applied, it will move to a new state, update the tape symbol (may or may not change), and move the head pointer to either right or left.
- q0 is the initial state.
- F is the set of final states. It is considered accepted when the input string reaches a state of F.
Let’s explain some examples of a Turing machine
Example 01: Turing Machine for Language L= “010”
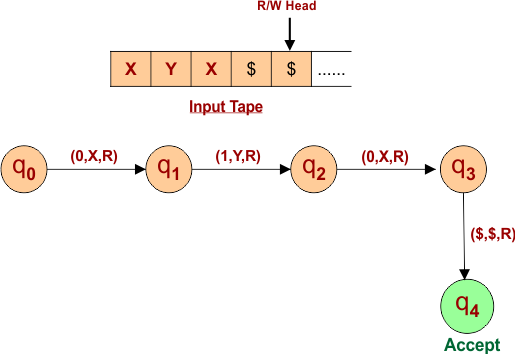
Let us construct a Turing machine for simple language L= “010”. The Input tape for language “010” will become as follows.

Special symbols are inserted after entering the language “010” into the input tape. This language is considered valid upon the arrival of the first special symbol.
Consider,
- Q = {q0,q1,q2,q3} where q0 is initial state.
- T = {0,1, X, Y,$} where $ represents blank.
- ∑ = {0,1}
- F = {q3}
| Important: Symbols “X and Y” In input Tape are used to Update values of Sigma input ∑ (0,1). It is just identification that tells that the input symbols are read successfully.(i.e., when reading Sigma input “0”, it should update with “X” in the input tap, and “1” should use “Y”). |
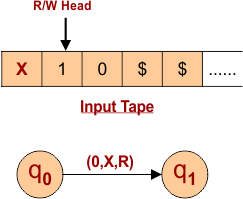
“0” for First Input Symol
- Transition goes to state (q1) from initial state (q0)
- The input tape’s first symbol, “0”, is updated to “X”.
- Read/Write Head Goes to One Position Right.
“1” for Second Input
- Transition goes to state (q2) from state (q1)
- The input tape’s second symbol, “1”, is updated to “Y”.
- Read/Write Head Goes to One Position Right.

“0” for Third Input
- Transition goes to state (q3) from state (q2)
- The third symbol on the input tape, which is currently “0,” is being changed to “X.”
- Read/Write Head Goes to One Position Right.
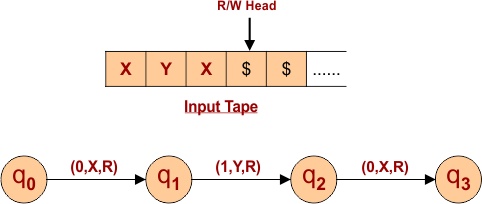
“$” for First Special Symbol
- The transition goes to state (q4) from state (q3), which is the accepting state.
- The special symbol “$” on the input tape remains unchanged.
- Read/Write Head Goes to One Position Right.
Other than the “010” language, all languages are rejected. All possible paths for each input (0,1 and $) at each state are given below.

Example 02: Turing machine for 0^N1^N
Design a Turing Machine that recognizes the language L = 0^N1^N where N>0
Solution
Given language (L = 0N1N) will generate an equal number of 0s and 1s. Consider the following input tap that contains L=000111.

Algorithm for language 0^N1^N (L = 0N1N)
Following is the algorithm for the above language in the Turing Machine.
- Step 01: Change 0 to X
- Step 02: Move Right to the First 1. If you do not find symbol (1), reject the language.
- Step 03: Change 1 to Y
- Step 04: Move Left to Leftmost 0
- Step 05: Repeat Steps 01 to 04 until no more 0 and 1 remain in the input tape.
Let’s construct a Turing Machine for a string 000111 of a given language.
According to Step 01, for the first input (0)
- The transition goes from the initial state (q0) to state (q1).
- The system converts the input tape’s first symbol, 0, to X.
- Read/Write head moves one step to the right side.

According to steps 2 and 3
R/W Head moves to the right To update the first symbol (1) on the right side of the input tape,
- Transition goes from state (q1) to state (q2).
- The system converts the input tape symbol,1, to Y.
- R/W Head Move one Position Left to update the Leftmost 0 in the next.
The following diagram shows that, at state q1, input 0 will keep the transition in the same state.

According to steps 4 and 01
R/W Head moves left to the leftmost (0) and updates it to (X).
- The transition goes from the state (q2) to state (q0) for input X.
- The system converts the Leftmost 0 of the input tape to X.
- After updating the Leftmost 0 to X, the R/W head moves toward the right side to update the upcoming 1.

Again, according to Steps 2 and 3
R/W Head moves to the right side to update the first symbol (1) on the right side of the input tape.
The following diagram shows the input tape and the Turing machine.

Again, according to Steps 4 and 01
Move Left to Leftmost 0 and update it to X.

Once again, according to steps 2 and 3
The R/W Head moves toward the right side to update the first symbol (1) on the right side of the input tape.

At this point,
- The input tape updates all 0s and 1s with X and Y, respectively.
- The current state is q2, and the R/W Head is moving toward the Left side of every input of Y.
- As X input occurs, the state goes to q0, and R/W Head moves toward the right side.
- By consuming all input Y, the state will be q3.
- As the first special symbol ($) occurs, the state goes to the final state (q4), and the R/W head will point to the last symbol of the considered language.
Hence, the following Turing machine is the acceptor of the given language.

Note: For special symbol ($), at state q0, the given language is accepted.
Turing Machine Example 3
Construct a TM for the language L = {0n} where n≥1
Solution
The following is the Regular expression for the given example
0(0)*
The following are the all possible strings created from L = {0n}
L= {0, 00, 000, 0000,…….}
Let’s suppose a string of “0000”. R/W head movement for input tap is given below

Finally, the turning machine to accept all possible strings over language L = {0n} where n≥1 is given below

Turing Machine Example 04:
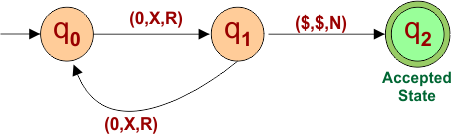
Construct a TM for the language L = {02n+1} where n≥0
Solution
The following is the Regular expression for the given example
0(00)*
The following are the all possible strings created from L = {02n+1}
L= {0, 000, 00000, 0000000,…….}
Let’s suppose a string of “000”. R/W head movement for input tap is given below

Finally, the turning machine to accept all possible strings over language L = {02n+1} where n≥0 is given below
Turing Machine Example 05:
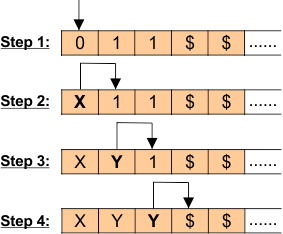
Construct a Turing machine that accepts all strings that start with 0.
Solution
The following is the Regular expression for the given example
0(0+1)*
The following are all the possible strings created
L= {0, 00, 01, 000, 011, …….}
Let’s suppose a string of “011”. R/W head movement for input tap is given below
Finally, the turning machine to accept all possible strings starts with “0”

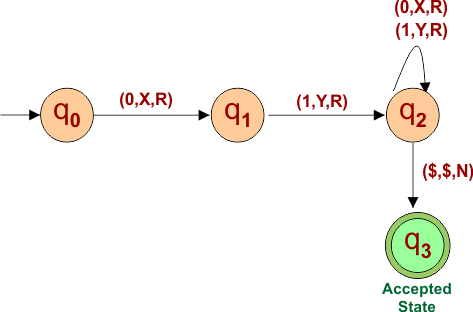
Turing Machine Example 06:
Construct a Turing machine that accepts all strings that start with 01.
Solution
The following is the Regular expression for the given example
01(0+1)*
The following are all the possible strings created
L= {01, 010, 011, 0100, 0111, …….}
Finally, the turning machine to accept all possible strings starts with “01” and is
Purpose of Turing Machine
Turing machines, Pushdown Automata (PDA), and Finite State Machines (FSM) are all models of computation. A Turing machine is more powerful than a PDA and an FSM regarding computational power, memory, language recognition, and applications. Let’s explain all of these comparisons in a table.
| Aspect | Turing Machine | Pushdown Automaton (PDA) | Finite State Machine (FSM) |
|---|---|---|---|
| Computational Power | Most powerful; can recognize any algorithmic process. | Less powerful; recognizes context-free languages (a subset of Turing Machine’s capability). | Least powerful; recognizes regular languages (a subset of context-free languages). |
| Memory | Uses infinite tape (unlimited memory). | Uses a stack for memory (limited but allows for more complexity than FSM). | Has a limited internal state with no external memory (stack or tape). |
| Language Recognition | Recognizes recursively enumerable languages (REL), including all regular, context-free, and recursively enumerable languages. | Recognizes context-free languages (including regular languages). | Recognizes only regular languages. |
| Applications | Primarily used in theoretical computer science to define algorithmic processes. | Used for parsing context-free grammars and analyzing programming languages/syntax. | Used in designing simple systems, such as control circuits. |













