Grammar in TOC
Grammar in TOC is a standard way of representing the language. The grammar contains a set of production rules that make up the language strings. The set of all possible strings that can be derived from a grammar is known as the language of that grammar. The symbol “G” mostly denotes grammar in TOC.
Real-Life Example of Grammar in TOC
Grammar is just the same as English Grammar. If the sentence is grammatically correct, it will be part of grammar; otherwise, it will not. The following is a real-life example of grammar in automata
- “I am going to school”. It is a valid example of grammar.
- I going am to school. It is not a valid example of grammar.
Elements of Grammar in TOC
To get a better understanding of grammar, we first understand its elements. Elements of Grammar depend on the types of grammar. The essential elements of grammar are given below.
G = (V, T, P, S) Where V, T, P, S are the elements of Grammar (G).
1. V (Variables also called Non-Terminal)
- Capital symbols represent a finite number of non-empty sets, i.e., A, B, C.
- It’s not a part of the string, which makes after-production rules.
2. T (Terminal)
- A finite set of Alphabets (Σ), Represented by small letters, i.e., a,b,c.
- All variables are replaced with non-terminals through production rules.
- Terminals are part of the string, which makes a production rule.
3. P (Production Rules)
- The finite set of non-empty rules to make a string of language
- i.e. P = { S → aSb , S → bSa , S → ∈ }
4. S (Start symbol)
The start symbol is used to start the production rule represented by S.
Note: Above grammar generates the strings through production rules having equal number of a’s and b’s. As given Below
L = {ab, aabb, aaabbb, …….}
Types of Grammar – Chomsky Hierarchy
An explanation of the four types of grammar is known as the Chomsky hierarchy. A diagram illustrating Chomsky’s hierarchy is provided below.

This means:
-
Every Regular Language is a Context-Free Language
-
Every Context-Free Language is a Context-Sensitive Language
-
Every Context-Sensitive Language is a Recursively Enumerable Language
But not vice versa:
- There exist Context-Free Languages that are not Regular
- There exist Context-Sensitive Languages that are not Context-Free
- There exist Recursively Enumerable Languages that are not Context-Sensitive
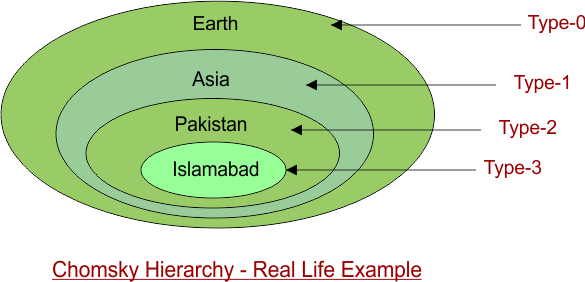
Chomsky Hierarchy – Real Life Example
- Just like Lahore is in Pakistan, and Pakistan is in Asia, and Asia is on Earth,
- Regular Languages are a subset of Context-Free Languages, which are in turn a subset of Context-Sensitive, and all of them are in the space of Recursively Enumerable Languages.
- But not all of Earth is Lahore
- Similarly, not all Recursively Enumerable Languages are Regular.
Chomsky Hierarchy – Table Summary
The following table explains all four types of grammar in TOC with detailed examples

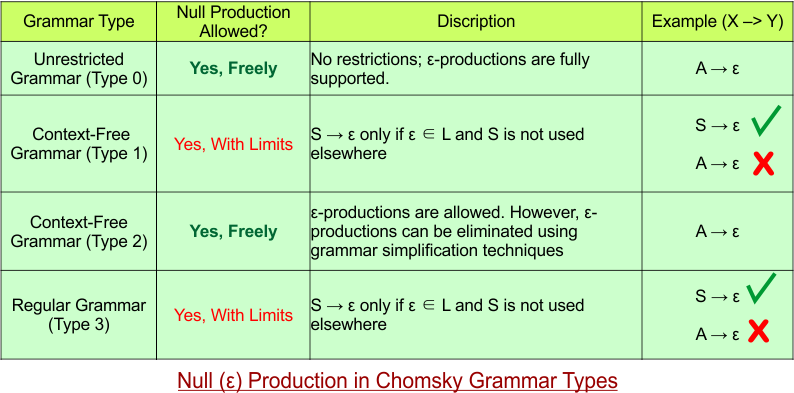
Null (ε) Production in Chomsky Hierarchy
In Chomsky Grammar, a null (ε) production is a rule where a non-terminal produces an empty string, following the table with a simple description.
There are three significant categories of grammar in TOC, as explained in the following diagram

Let’s explain the major types of grammar based on types of production rules.
1. Regular Grammar (RL)
Regular Grammar generates the Regular Languages, and the Finite Automata Machine accepts all regular languages. It is also called Type-3 grammar.
![]()
Regular languages are of two types.
- Finite Regular Languages
- Infinite Regular Languages
Finite Automata Machine is also of two types
- Deterministic Finite Automata (DFA)
- Non-Deterministic Finite Automata (NDFA)
| All regular languages, either finite or infinite, are accepted by NDFA. However, all regular languages and some infinite languages are accepted by DFA. |
2. Context Free Grammar (CFG)
Context-free Grammar generates Context-free Languages, and the Pushdown Automata Machine accepts all context-free languages. Context-free Grammar is also called Type-2 grammar.

Context Free languages are of two types
- Deterministic Context-Free Languages
- Non-deterministic Context-Free Languages
Pushdown Automata Machine is also of two types
- Deterministic Pushdown Automata (DPDA)
- Non-Deterministic Pushdown Automata (NPDA)
| All Deterministic Context-Free languages are accepted by Deterministic Pushdown Automata (DPDA). But all Non-Deterministic Context-Free languages are accepted by Non-Deterministic Pushdown Automata (NPDA). |
3. Context Sensitive Grammar (CSG)
Context-sensitive Grammar generates context-sensitive languages, and linear bound automata machines accept all context-sensitive languages. Context-free Grammar is also called Type-1 grammar.

Note: Context-sensitive languages and their machines are not deterministic or non-deterministic.
4. Unrestricted Grammar
Unrestricted Grammar generates the Recursive enumerable Languages, and the Turing Machine accepts all Recursive enumerable languages. It is also called Type-0 grammar.

| Necessary: Type-0 Accepter has the Highest Power, and Type-3 accepter has the lowest Power. It means type -3 accepted, which means Turing Machine can accept all languages, whether regular, context-free, or context-sensitive. However, the Type-3 accepter, Finite Automata, can accept only regular languages. |
Example of Grammar in Automata
Consider a grammar G = (V, T, P, S) where
- V = { S } // Set of Non-Terminal symbols
- T = { 0 , 1 } // Set of Terminal symbols
- P = { S → 0S1S , S → 1S0S , S → ∈ } // Set of production rules
- S = { S } // Start symbol
This grammar generates the strings having an equal number of 0’s and 1’s.
Equivalent Grammars in TOC
Two grammars will be equivalent if and only if they both generate the same languages.
Grammar G1: Consider Grammar 1 (G1) with the following production Rules.
- S → aSb
- S → ∈
Grammar G2: Consider Grammar 2 (G2) with the following production Rules.
- S → aAb / ∈
- A → aAb / ∈
Result: The above Grammar (G1 and G2) will generate the same language.
L = { anbn , n>=0 }
So, L(G1) = L(G2).
It can be represented as
∴ G1 ≡ G2













