Examples of DFA
This lecture discusses more than 50 examples of a DFA. But you make sure that you have already covered the topic of Deterministic Finite Automata. There are seven different categories selected for examples of DFA.
Let’s explain all the various questions of DFA using various categories
DFA Question Category 1: Accept Only the Given Input
In this section, a DFA accepts only one specific input string and rejects all other strings. For example,
- Accepts only the string “aaab”
- Accepts only the string “01”
DFA Example: 1.1
DFA Question: Construct a DFA with ∑ = {a, b} that accepts only the input “aaab”.
Solution
The following diagram represents the DFA that accepts only the input “aaab”.
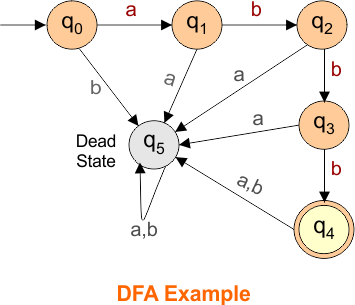
The explanation of the above DFA is given below
- States = {q0, q1, q2, q3, q4, q5}
- Input Alphabet = {a, b}
- Initial State = q0
- Final State = q4
- Dead State = q5
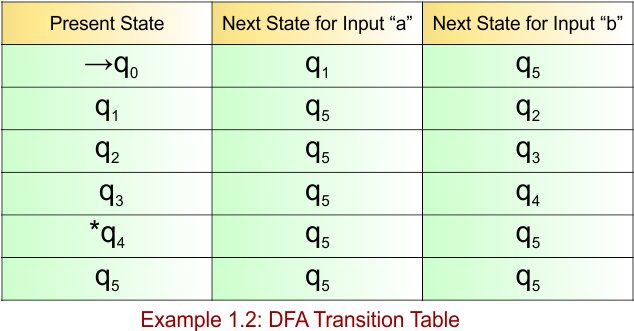
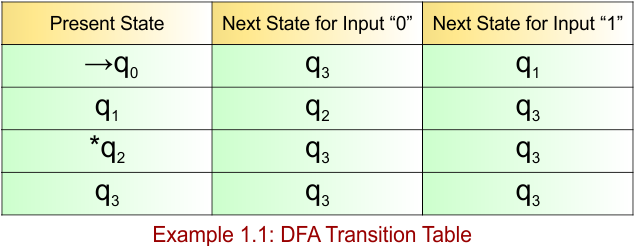
Transition Function (δ) for all input alphabets (“a,b”) is defined in the following DFA Transition Table
DFA Example: 1.2
Solution:
DFA that accepts only the input string “10” is given below
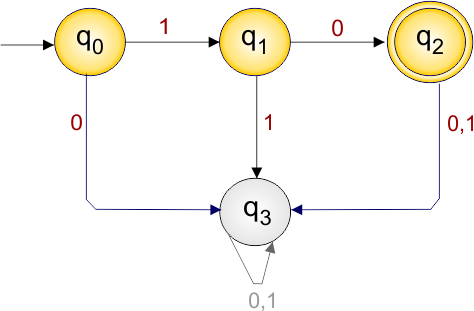
The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {0,1}
- Initial State = q0
- Final State = q2
- Dead State = q3
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
Don’t confuse: Dead state is also called trap or rejected state and can be represented as qd, qϕ, or any other notation.
DFA Question Category 2: Starts and Ends With
DFA accepts strings that start with a specific substring and/or end with a specific substring. For Examples
- Starts with 01
- Ends with 000
- Starts with a, ends with bb
- Starts and ends with the same symbol
DFA Example: 2.1
DFA Question: Construct a DFA that accepts all the strings over the alphabet ∑ {0,1} that start with “0”.
Solution:
The DFA example 2.1 provides the following
- Regular Expression = 0(0+1)*
- Accepted Strings = {0, 01, 00, 010, 011, 000, 001,…, }
- Some Rejected Strings = {ε, 1, 11, 101, 1001, 110}
Let’s draw the DFA that accepts all strings starting with “0”.
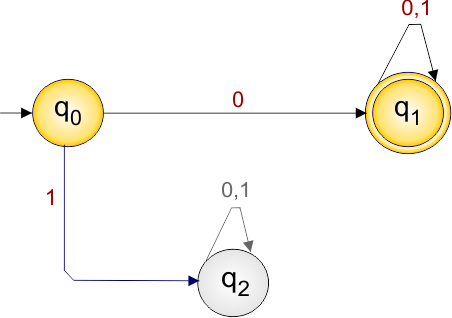
The explanation of the above DFA is given below
- States = {q0, q1, q2 }
- Input Alphabet = {0, 1}
- Initial State = q0
- Final States = {q1}
- Dead State = q2
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 2.2
DFA Question: Construct a DFA that accepts all the strings over alphabet ∑ {0,1} that start with “01”.
Solution:
DFA, which accepts all the strings over the alphabet ∑ {0,1} that start with “01”. provides the following
- Regular Expression = 01(0+1)*
- Accepted Strings = {01, 010, 011, 0100, 0111, 01101, …}
- Some Rejected Strings = {ε, 0, 1, 10, 00, 11, 001, 101}
Let’s draw the DFA that accepts all the strings of the above language
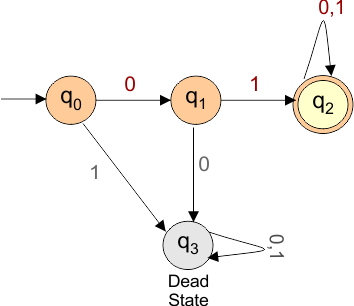
The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final States = q2
- Dead State = q3
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
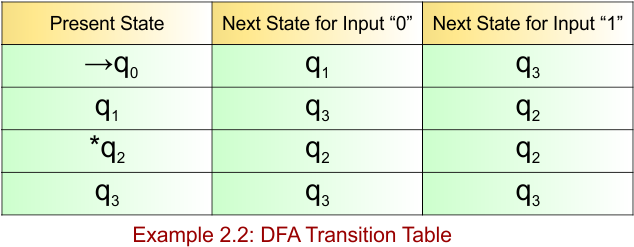
DFA Example: 2.3
DFA Question: Construct a DFA that accepts all the strings over the alphabet ∑ {0,1} that end with “0”.
Solution:
DFA, which accepts all the strings over alphabet ∑ {0,1} that end with “0”, provides the following
- Regular Expression = (0+1)*0
- Accepted Strings = {0, 10, 110, 000, 1010, 1110, …}
- Some Rejected Strings = {ε, 1, 11, 101, 1001, 111}
Let’s draw the DFA, which accepts all the strings that end with “0”.

The explanation of the above DFA is given below
- States = {q0, q1}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q1
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
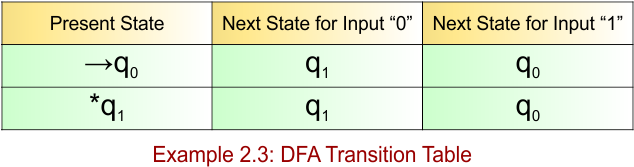
Example: 2.4
DFA Question: Construct a DFA that accepts all the strings over the alphabet ∑ {0,1} that end with “10”.
Solution:
DFA, which accepts all the strings over the alphabet ∑ {0,1} that end with “10”, provides the following
- Regular Expression = (0+1)*10
- Accepted Strings = {10, 010, 110, 0010, 1110, 1010, …}
- Some Rejected Strings = {ε, 0, 1, 11, 00, 100, 101, 111}
DFA, which accepts all the strings that end with “10” is given under

The explanation of the above DFA is given below
- States = {q0, q1, q2}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q2
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
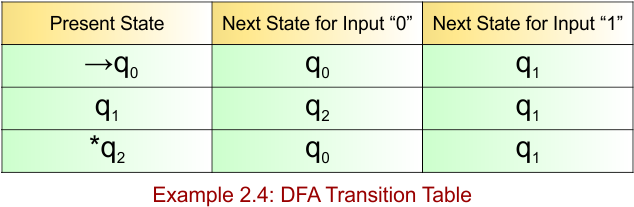
DFA Example: 2.5
DFA Question: Construct a DFA with sigma ∑ = {0, 1}, accepts those string that starts with “1” and ends with “0”.
Solution:
The DFA example 2.5 provides the following
- Regular Expression (RE) = 1(0+1)*0
- Accepted Strings (L) = {10, 100, 110, 1010, 1110, 10010, …}
- Some Rejected Strings (REJ_Str) = {ε, 0, 1, 11, 00, 101, 111, 010}
The required DFA diagram, for example 2.5, is given below
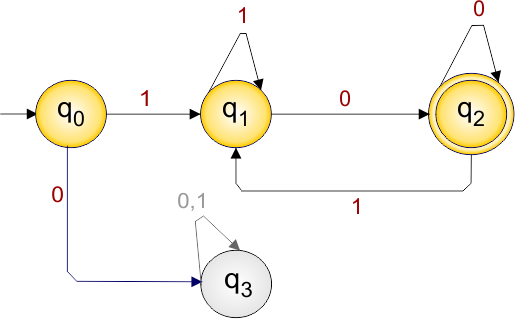
The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = {q2}
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 2.6
DFA Question: Construct a DFA with sigma ∑ = {0, 1} for the language accepting strings ending in either ’01’ or ’10’.
Solution:
The DFA example 2.6 provides the following
- Regular Expression = (0+1)*(01 + 10)
- Accepted Strings = {01, 10, 101, 110, 001, 1110, 1001, …}
- Some Rejected Strings = {ε, 0, 1, 00, 11, 100, 111, 1010 }
The required DFA diagram, for example 2.6, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2, q3, q4}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final States = {q2, q4}
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 2.7
DFA Problem: Construct a DFA with sigma ∑ = {0, 1} for the language accepting strings starting and ending with ‘0’ always.
Solution:
The DFA example 2.7 provides the following
- Regular Expression = 0(0+1)*0
- Accepted Strings = {00, 010, 000, 0111110, 0010, 0101010, …}
- Some Rejected Strings = {ε, 1, 01, 10, 11, 011, 100, 101}
The required DFA diagram, for example 2.7, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = {q1}
- Dead State = q3
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 2.8
DFA Question: Design a DFA with sigma ∑ = {0, 1} for the language accepting strings starting and ending with different characters.
Solution:
The DFA example 2.8 provides the following
- Regular Expression = (0(0+1)*1) + (1(0+1)*0)
- Accepted Strings = {01, 10, 001, 110, 1010, 100, 01101, …}
- Some Rejected Strings = {ε, 0, 1, 00, 11, 010, 101, 111}
The required DFA diagram, for example 2.8, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2, q3, q4}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = {q2, q4}
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
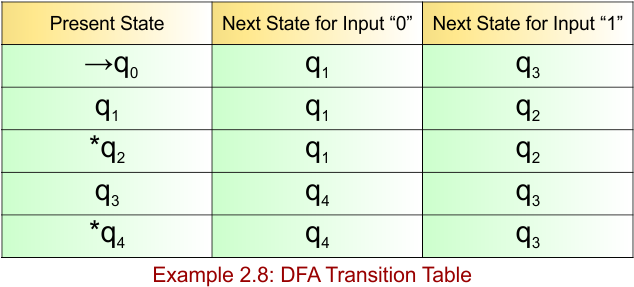
DFA Example: 2.9
DFA Question: Construct a DFA with sigma ∑ = {0, 1} for the language accepting strings starting and ending with the same characters.
Solution:
The DFA example 2.9 provides the following
- Regular Expression = (0(0+1)*0) + (1(0+1)*1)
- Accepted Strings = {00, 11, 010, 101, 0110, 1001, …}
- Some Rejected Strings = {ε, 01, 10, 001, 110, 011, 100}
The required DFA diagram, for example 2.9, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2, q3, q4}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = {q2, q4}
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
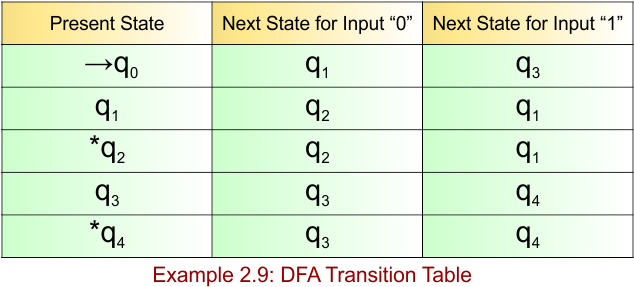
DFA Example: 2.10
DFA Question: Construct a DFA with sigma ∑ = {0, 1} for the language accepting strings starting with ‘00’ or ’11’
Solution:
The DFA example 2.10 provides the following
- Regular Expression = (00 + 11)(0+1)*
- Accepted Strings = {00, 11, 001, 110, 0000, 1111, 00101, 11010, …}
- Some Rejected Strings = {ε, 0, 1, 01, 10, 010, 101, 1001}
The required DFA diagram, for example 2.10, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2, q3, q4}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q3
- Dead State = q4
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
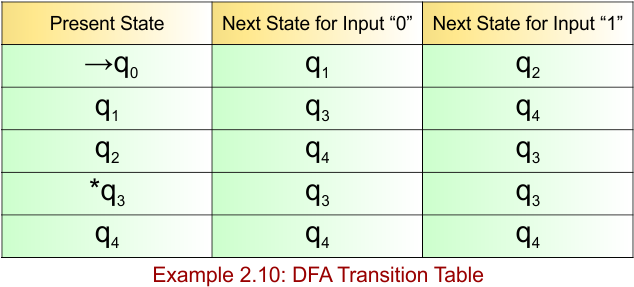
DFA Example: 2.11
DFA Question: Construct a DFA with sigma ∑ = {0, 1} for the language accepting strings ending with ‘0011’.
Solution:
The DFA example 2.11 provides the following
- Regular Expression = (0+1)*0011
- Accepted Strings = {0011, 10011, 000011, 110011, 1010011, …}
- Some Rejected Strings = {ε, 0, 1, 001, 011, 00110, 1100, 1010}
The required DFA diagram, for example 2.11, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2, q3, q4}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q4
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
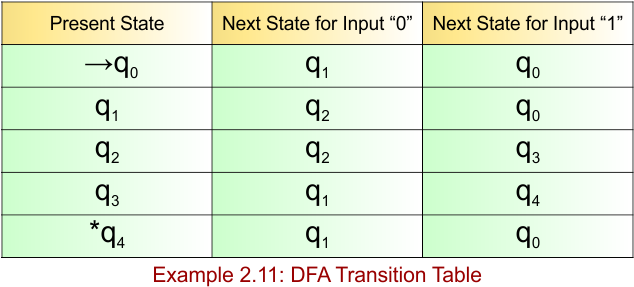
DFA Example: 2.12
DFA Question: Construct a DFA with sigma ∑ = {0, 1} for the language accepting strings ending with ‘0110’.
Solution:
The DFA example 2.12 provides the following
- Regular Expression = (0+1)*0110
- Accepted Strings = {0110, 10110, 0000110, 1100110, 10010110, …}
- Some Rejected Strings = {ε, 0, 1, 011, 110, 01101, 0010, 1110}
The required DFA diagram, for example 2.12, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2, q3, q4}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q4
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
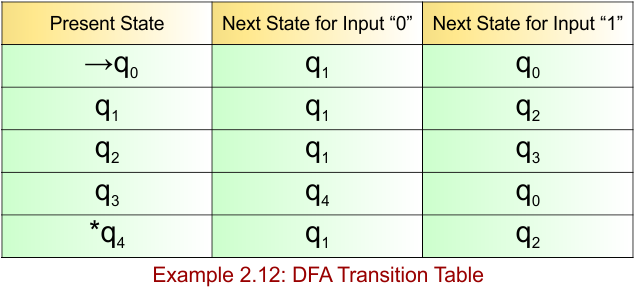
DFA Example: 2.13
DFA Question: Construct a DFA with sigma ∑ = {0, 1} for the language accepting strings ending with ‘00’.
Solution:
The DFA example 2.13 provides the following
- Regular Expression = (0+1)*00
- Accepted Strings = {00, 100, 1100, 0100, 11100, 00100, …}
- Some Rejected Strings = {ε, 0, 1, 01, 10, 001, 101, 1001}
The required DFA diagram, for example 2.13, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q2
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
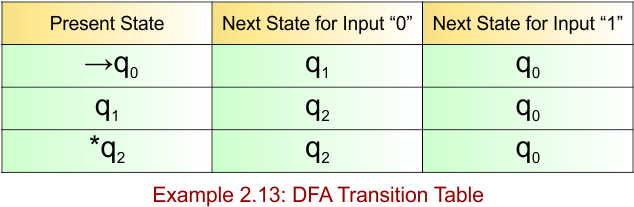
DFA Question Category 3: Contains Substring
DFA accepts strings that contain a specific substring anywhere in the string. For Examples
- Contains 101
- Contains ababa
- Contains 000
DFA Example: 3.1
DFA Question: Construct a DFA that accepts all the strings over ∑ {0,1} where each contains “0” and always starts with “1”.
Solution:
The given question provides the following
- Regular Expression =1*0(0+1)*
- Accepted Strings = {10, 101, 100, 1001, 10011, 110, 1010, …}
- Some Rejected Strings = {ε, 0, 01, 011, 111}
The required DFA diagram, for example 2.5, is given below

The explanation of the above DFA is given below
- States = {q0, q1}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q1
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 3.2
DFA Question: Construct a DFA that accepts all the strings over alphabet ∑ {0,1} where each string contains “00”.
Solution:
The given question provides the following
- Regular Expression = (0+1)*00(0+1)*
- Accepted Strings = {00, 001, 100, 1100, 000, 1001, 0010, …}
- Some Rejected Strings = {ε, 0, 1, 01, 10, 11, 101, 0101}
The required DFA diagram, for example 3.2, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q2
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 3.3
DFA Question: Construct a DFA with sigma ∑ = {0, 1}, accepts all strings that contain three consecutive 0’s.
Solution:
The given DFA example 3.3 provides the following
- Regular Expression = (0+1)*000(0+1)*
- Accepted Strings = {000, 1000, 0001, 10001, 0000, 110001, …}
- Some Rejected Strings = {ε, 0, 00, 1, 010, 1010, 0010, 01010}
DFA, which accepts all the strings that contain three consecutive 0’s, is given under
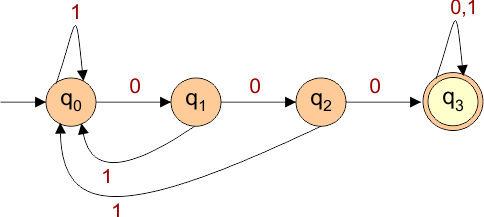
The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q3
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
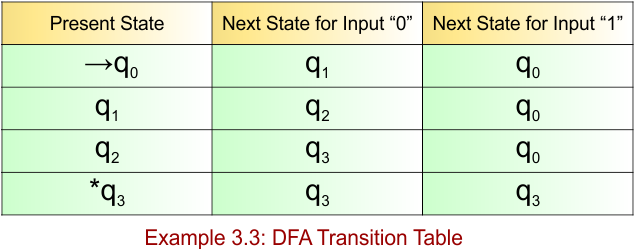
DFA Example: 3.4
DFA Question: Construct a DFA with sigma ∑ = {0, 1}, accepts all strings that do not contain three consecutive 0’s.
Solution:
The given DFA example 3.4 provides the following
- Regular Expression = ((1+01+001)* (ε + 0 + 00))
- Accepted Strings = {ε, 0, 1, 01, 10, 001, 1001, 100100, …} (no “000” as a substring)
- Some Rejected Strings = {000, 1000, 0001, 0000, 10001, 010001}
The required DFA diagram, for example 3.4, is given below
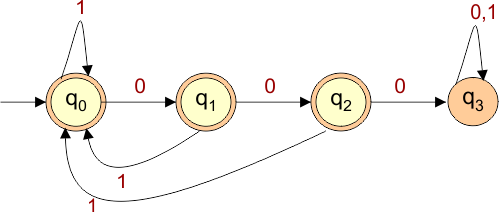
The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = {q0,q1,q2}
- Dead state = q3
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 3.5
DFA Question: Construct a DFA that accepts all the strings over the alphabet ∑ {0,1} where each string contains “101” as a substring.
Solution:
The given DFA example 3.5 provides the following
- Regular Expression = (0+1)*101(0+1)*
- Accepted Strings = {101, 0101, 1010, 1101, 00101, 10111, …}
- Some Rejected Strings = {ε, 0, 1, 10, 01, 100, 110, 1111}
Let’s draw the DFA that accepts all the strings of the above language
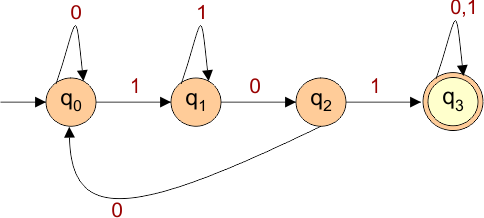
The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q3
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 3.6
DFA Question: Construct a DFA for the language that accepts strings containing neither ’00’ nor ’11’ as a substring over the input alphabet ∑ = {0, 1}.
Solution:
The given DFA example 3.6 provides the following
- Regular Expression = (01 + 10)*
- Accepted Strings = {ε, 0, 1, 01, 10, 010, 101, 0101, 1010, …} (no “00” or “11” as substrings)
- Some Rejected Strings = {00, 11, 001, 110, 0110, 1000, 111, 000}
The required DFA diagram, for example 3.6, is given below
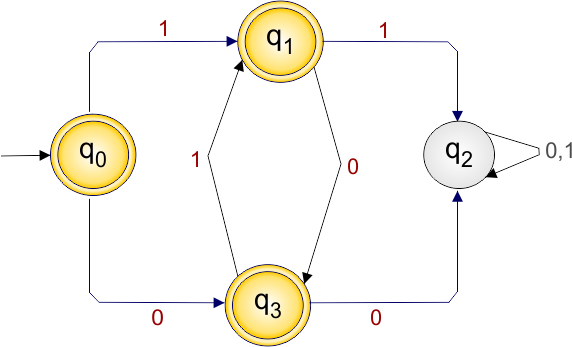
The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = {q0, q1, q3}
- Dead State = q2
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 3.7
DFA Question: Construct a DFA that accepts strings that must contain ’01’ or ’10’ as a substring over input alphabets ∑ = {0, 1}.
Solution:
The given DFA example 3.7 provides the following
- Regular Expression = (0+1)*(01 + 10)(0+1)*
- Accepted Strings = {01, 10, 001, 110, 1010, 010, 1001, …} (must contain “01” or “10”)
- Some Rejected Strings = {ε, 0, 1, 00, 11, 000, 111, 0000, 1111}
The required DFA diagram, for example 3.7, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2, q3, q4, q5}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = {q2,q4,q5}
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
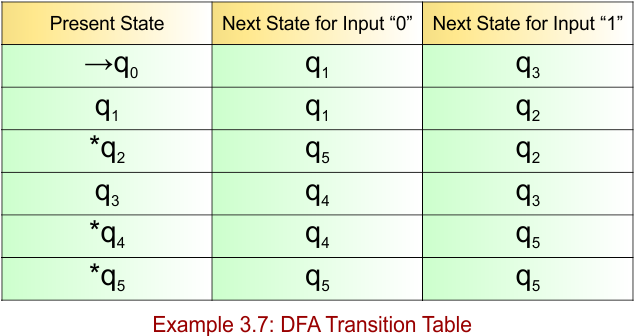
DFA Example: 3.8
DFA Question: Construct a DFA with sigma ∑ = {0, 1} for the language accepting strings containing exactly two ‘0’.
Solution:
The given DFA example 3.8 provides the following
L={00, 100, 001, 1010, 0101, 11100,…….}
The required DFA diagram, for example 3.8, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q2
- Dead state = q3
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 3.9
DFA Question: Construct a DFA with sigma ∑ = {0, 1} for the language accepting strings containing at least two ‘0’.
Solution:
The given DFA example 3.9 provides the following
- Regular Expression = (1)*0(1)*0(1)*
- Accepted Strings = {00, 001, 010, 100, 10101, 1010, 0110, 10101, …} (exactly two 0s)
- Some Rejected Strings = {ε, 0, 1, 000, 111, 0100, 0010, 1000}
The required DFA diagram, for example 3.9, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q2
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 3.10
DFA Question: Construct a DFA with sigma ∑ = {0, 1} for the language accepting strings containing at most two ‘0’.
Solution:
The given DFA example 3.10 provides the following
- RE = 1* + 1*01* + 1*01*01*
- Accepted Strings = {ε, 1, 11, 0, 10, 01, 101, 001, 010, 100, 011, 110, …} (strings with 0, 1, or 2 zeros only)
- Some Rejected Strings = {000, 1000, 0001, 01000, 11000, 0000, 0010}
The required DFA diagram, for example 3.10, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = {q0, q1, q2}
- Dead state = q3
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 3.11
DFA Question: Construct a DFA with sigma ∑ = {0, 1} for the language accepting strings containing an odd number of total zeros (or odd binary numbers strings).
Solution:
The given DFA example 3.11 provides the following
- Regular Expression = (1*01*01*)*1*0(1*01*01*)*
- Accepted Strings = {0, 10, 01, 1000, 0001, 1110, 00101, …} (strings with 1, 3, 5, … zeros)
- Some Rejected Strings = {ε, 1, 11, 00, 1010, 1100, 00, 1010}
The required DFA diagram, for example 3.11, is given below

The explanation of the above DFA is given below
- States = {q0, q1}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q1
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
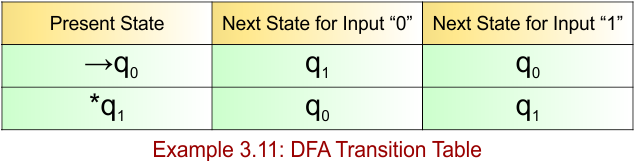
DFA Example: 3.12
DFA Question: Construct a DFA for the Language (L) that accepts only the strings where every “00” is Immediately Followed by 1 over the input alphabet ∑= {0,1}
Solution:
The given DFA example 3.12 provides the following
- Valid Strings: L = { 001, 1001, 01001, … }
- Invalid Strings: Not in L = { 00, 000, 0000, 1000, 10100011, … }
The required DFA diagram, for example 3.12, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2, q3, q4}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q3
- Dead State = q4
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
DFA Question Category 4: Specific Length
DFA accepts strings of exactly n characters. For Examples
- Strings of length 3
- Binary strings of length 5
- Strings over {a, b} of length 2
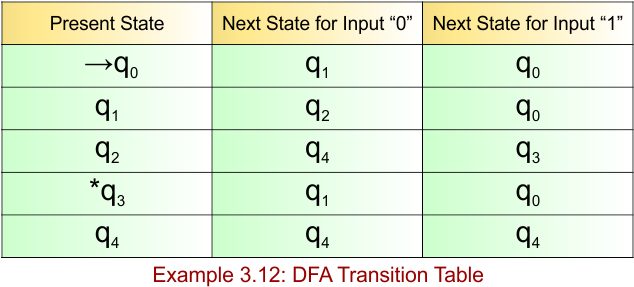
DFA Example: 4.1
DFA Question: Construct a DFA, which accept all the string over alphabets ∑ {0,1} where the length of each string is exactly 2.
Solution:
The given DFA example 4.1 provides the following
- Regular Expression = (0+1)(0+1)
- Accepted Strings = {00, 01, 10, 11} (all strings of length exactly 2)
- Some Rejected Strings = {ε, 0, 1, 000, 0110, 1011, 111, 1001}
The following diagram represents the DFA accepter for the language language where the length of each string is exactly two.

The explanation of the above DFA is given below
- States = {q0, q1, q2, qϕ}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q2
- Dead State = qϕ
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
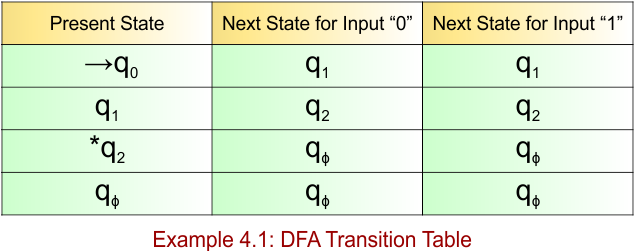
DFA Example: 4.2
DFA Question: Construct a DFA that accepts all the strings over alphabet ∑ {0,1} where the length of each string is ≥ 2.
Solution:
The given DFA example 4.2 provides the following
- Regular Expression = (0+1)(0+1)(0+1)*
- Accepted Strings = {00, 01, 10, 11, 000, 010, 101, 111, 1100, …} (all strings with length ≥ 2)
- Some Rejected Strings = {ε, 0, 1}
The following diagram represents the DFA acceptor for the language where the length of each string is ≥ 2.

The explanation of the above DFA is given below
- States = {q0, q1, q2}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q2
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 4.3
DFA Question: Construct DFA, which accept all the string over alphabets ∑ {0,1} where the length of each string is ≤ 2
Solution:
The given DFA example 4.3 provides the following
- Regular Expression = ε + (0+1) + (0+1)(0+1)
- Accepted Strings = {ε, 0, 1, 00, 01, 10, 11} (all strings of length ≤ 2)
- Some Rejected Strings = {000, 1010, 111, 001, 0101}
The following diagram represents the DFA acceptor for the language where the length of each string is ≤ 2
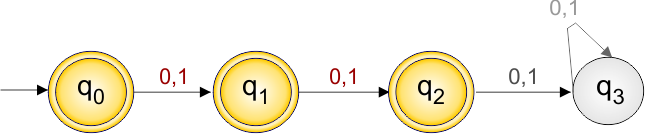
The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = {q0, q1, q2}
- Dead state = q3
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
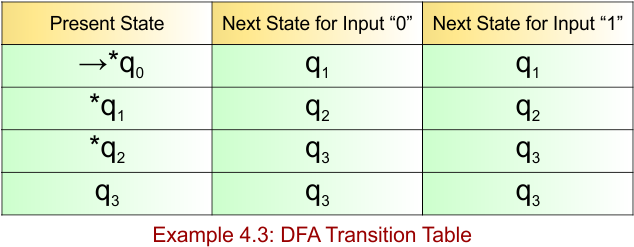
DFA Example: 4.4
DFA Question: Construct a DFA over w {a,b}* such that length of “a” is greater or equals to 2 and there is no restriction over length of b.
Solution:
The given DFA example 4.4 provides the following
- Accept strings like: aa, aab, aba, baa, bababaa, bbaabb, etc.
- Reject strings like: Epsilon, b, ab, a, bbabbbb (zero or one a)
- RE = (a + b)*a(a + b)*a(a + b)*
The required DFA diagram, for example 4.4, is given below
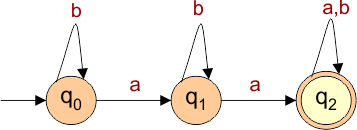
The explanation of the above DFA is given below
- States = {q0, q1, q2}
- Input Alphabet = {a, b}
- Initial State = q0
- Final State = q2
Transition Function (δ) for all input alphabets (“a,b”) is defined in the following DFA Transition Table
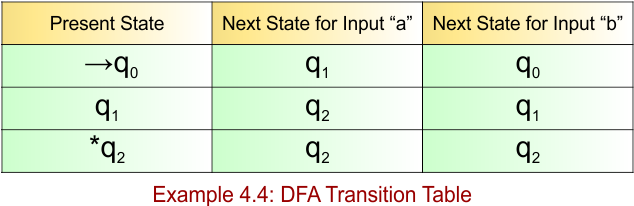
DFA Example: 4.5
DFA Question: Construct a DFA over w {a,b}* such that the length of “a” must be 2 and there is no restriction over length of b.
Solution:
The given DFA example 4.5 provides the following
- Regular Expression = b*a b*a b*
- Accepted Strings = {aa, baa, aba, aab, baba, abba, bbaab, …} (strings with exactly two ‘a’s, anywhere in the string, b’s allowed anywhere and in any number)
- Some Rejected Strings = {ε, b, bb, a, aaa, abaa, baaa, ababaa, …} (less than or more than two ‘a’s)
The required DFA diagram, for example 4.5, is given below

The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {a,, b}
- Initial State = q0
- Final State = q2
- Dead state = q3
Transition Function (δ) for all input alphabets (“a,b”) is defined in the following DFA Transition Table
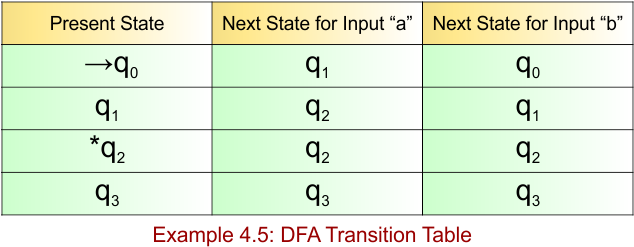
DFA Example: 4.6
DFA Question: Construct a DFA which accept all the string over alphabets ∑ {0,1} where the length of each string is EVEN.
Solution:
The given DFA example 4.6 provides the following
- Regular Expression = ((0+1)(0+1))*
- Accepted Strings = {ε, 00, 01, 10, 11, 0000, 0101, 1100, 1111, …} (strings with even length: 0, 2, 4, …)
- Rejected Strings = {0, 1, 000, 011, 101, 111, 1001, 010, …} (strings with odd length)
The following diagram represents the DFA acceptor for the language where the length of each string is even.

The explanation of the above DFA is given below
- States = {q0, q1}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q0
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 4.7
DFA Question: Construct DFA, which accept all the string over alphabets ∑ {0,1} where the length of each string is ODD.
Solution:
The given DFA example 4.7 provides the following
- Regular Expression = (0+1)((0+1)(0+1))*
- Accepted Strings = {0, 1, 000, 010, 101, 111, 001, 10001, …} (strings with odd length: 1, 3, 5, …)
- Some Rejected Strings = {ε, 00, 01, 10, 11, 0000, 0101, 1100} (strings with even length)
The following diagram represents the DFA accepter for the language where the length of each string is odd.

The explanation of the above DFA is given below
- States = {q0, q1}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q1
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
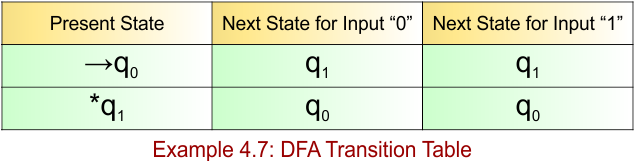
DFA Example: 4.8
DFA Question: Construct a DFA with sigma ∑ = {0, 1}, accepts those strings that have an even number of “0’s” and an even number of “1’s”.
Solution:
The given DFA example 4.8 provides the following
- Regular Expression: No simple RE exists for this pattern, but a conceptual structure is: ((00 + 11 + (01 + 10)(01 + 10)))*
- Accepted Strings: {ε, 0011, 1100, 0101, 1001, 0110, 1010, 00001111, …} (even number of 0s and even number of 1s)
- Some Rejected Strings: {0, 1, 01, 10, 000, 111, 001, 011, 110} (strings with odd number of 0s or 1s)
Note: Epsilon (ε) represents zero, which is even.
Let’s draw the DFA that accepts all the strings of the above language

The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q0
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
In Above DFA,
- If state q1 becomes final instead of q0, the DFA will accept all those strings with Odd “0” and even “1”.
- And if state q2 becomes final instead of q0, then the DFA will accept all those strings with even “0” and odd “1”.
- And If state q3 becomes final instead of q0, then the DFA will accept all those strings with odd “0” and odd “1”.

DFA Question Category 5: Divisibility (Binary Numbers)
DFA accepts binary strings whose decimal representation is divisible by a number. For Examples
- Binary strings divisible by 2
- Divisible by 3 (mod 3)
- Divisible by 5
DFA Example 5.1
DFA Problem: Construct a DFA that accepts the set of all strings over {0, 1} when interpreted as a binary number that is divisible by 2.
Solution:
The given DFA example 4.1 provides the following
- Regular Expression = (0 + 1)*(0)
- Accepted Strings = {0, 10, 100, 110, 1010, 1110, …} (binary strings ending in 0 → divisible by 2)
- Some Rejected Strings = {1, 11, 101, 111, 1001, 1101, …} (binary strings ending in 1 → not divisible by 2)
Explanation (Example for 100):
Binary 100 = Decimal 4
Since 4 ÷ 2 = 2, it is divisible by 2.
Binary to Decimal Table (Divisible by 2):
| Binary | Decimal | Divisible by 2? |
|---|---|---|
| 0 | 0 | Yes |
| 10 | 2 | Yes |
| 100 | 4 | Yes |
| 110 | 6 | Yes |
| 1 | 1 | No |
| 11 | 3 | No |
The following diagram represents the DFA that accepts only binary integers divisible by 2

The explanation of the above DFA is given below
- State = {q0, q1}
- Input Alphabet = {0,1}
- Initial State = {q0}
- Final States = {q0}
Transition Function (δ) for the input alphabet (“0”, “1”) is defined in the following DFA Transition Table
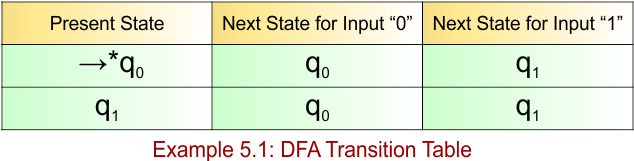
DFA Example: 5.2
DFA Problem: Construct DFA, which accepts all the string over alphabets ∑ {0,1} where binary integers divisible by 3
Solution:
The given DFA example 5.2 provides the following
- Accepted Strings = {0, 11, 110, 1001, 1100, 1111, 10010, …} (binary numbers divisible by 3)
- Some Rejected Strings = {1, 10, 101, 1110, 100, 1010, 1001, 111} (binary numbers not divisible by 3)
The explanation for string 1001 is given below.
1001= 9, 9/3 = 3; hence, 1001 is divisible by 3.
Binary to Decimal Table (Divisible by 3):
| Binary | Decimal | Divisible by 3? |
|---|---|---|
| 0 | 0 | Yes |
| 11 | 3 | Yes |
| 110 | 6 | Yes |
| 1001 | 9 | Yes |
| 1100 | 12 | Yes |
| 1111 | 15 | Yes |
| 10010 | 18 | Yes |
| 1010 | 10 | No |
| 1011 | 11 | No |
The following diagram represents the DFA acceptor for the language where binary integers are divisible by three.

The explanation of the above DFA is given below
- State = {q0, q1, q2}
- Input Alphabet = {0,1}
- Initial State = {q0}
- Final States = {q0}
Transition Function (δ) for the input alphabet (“0”, “1”) is defined in the following DFA Transition Table

DFA Example: 5.3
DFA Problem: Construct DFA that accepts all the strings over alphabet ∑ {0,1} where binary integers are divisible by 4
Solution:
The given DFA example 5.3 provides the following
- Regular Expression = (0+1)*00
- Accepted Strings = {0, 100, 1000, 1100, 10000, 100100, …} (binary integers divisible by 4)
- Some Rejected Strings = {1, 10, 11, 101, 111, 1010, 1101, 1001} (binary integers not divisible by 4)
The given question provides the following language
L = { 0, 100, 1000, 1100, 10000, 11000, 11100, … }
The explanation for string 10000 is given below.
10000= 16, 16/4 = 4, hence 10000 is divisible by 4.
Binary to Decimal Table (Divisible by 4):
| Binary | Decimal | Divisible by 4? |
|---|---|---|
| 0 | 0 | Yes |
| 100 | 4 | Yes |
| 1000 | 8 | Yes |
| 1100 | 12 | Yes |
| 10000 | 16 | Yes |
| 10010 | 18 | No |
| 11011 | 27 | No |
The following diagram represents the DFA accepter for the language where binary integers are divisible by four.

The explanation of the above DFA is given below
- State = {q0, q1, q2, q3}
- Input Alphabet = {0,1}
- Initial State = {q0}
- Final States = {q0}
Transition Function (δ) for the input alphabet (“0”, “1”) is defined in the following DFA Transition Table
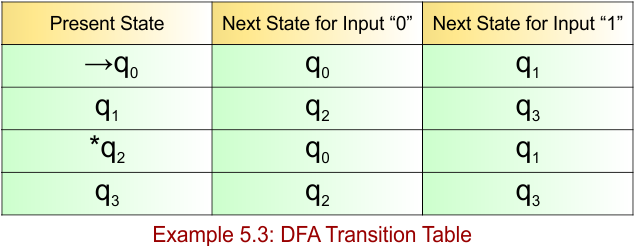
DFA Example: 5.4
DFA Problem: Construct a DFA that accepts the set of all strings over {0, 1} when interpreted as a binary number, that is, divisible by 5.
Solution:
The given DFA example 5.4 provides the following
L = { 0, 101, 1010, 1111, 10100, 11001, 11110, … }
Note: Regular Expression is not expressible concisely with standard regular expressions (requires modulo-5 tracking via DFA)
| Binary | Decimal | Divisible by 5? |
|---|---|---|
| 0 | 0 | yes |
| 101 | 5 | yes |
| 1010 | 10 | yes |
| 1111 | 15 | yes |
| 10100 | 20 | yes |
| 100000 | 32 | no |
| 100101 | 37 | no |
Required DFA is,
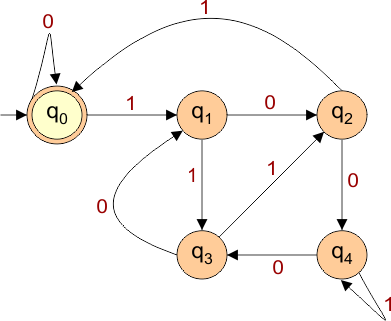
The explanation of the above DFA is given below
- State = {q0, q1, q2, q3, q4}
- Input Alphabet = {0,1}
- Initial State = {q0}
- Final States = {q0}
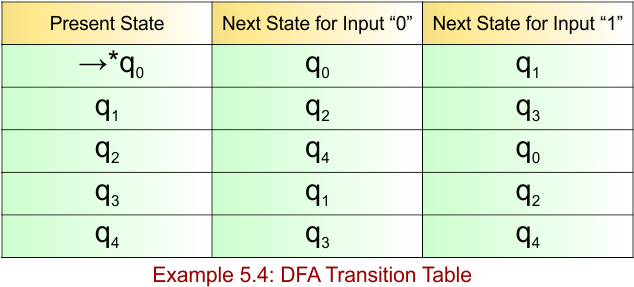
Transition Function (δ) for the input alphabet (“0”, “1”) is defined in the following DFA Transition Table
DFA Question Category 6: General DFA Examples
Let’s discuss some general examples of DFA
DFA Example: 6.1
DFA Problem: Draw a DFA for to accept any number of “a” over the input alphabet Σ = {a}
Solution:
The given DFA example 6.1 provides the following
- Regular Expression = a*
- Accepted Strings = {ε, a, aa, aaa, aaaa, …} (any number of ‘a’, including none)
- Some Rejected Strings = {b, ab, ba, aab, bbb} (any string containing symbols other than ‘a’)
The required DFA diagram, for example 6.1, is given below
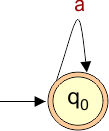
The explanation of the above DFA is given below
- State = q0
- Input Alphabet = a
- Initial State = q0
- Final States = q0
Transition Function (δ) for input alphabet (“a”) is defined in the following DFA Transition Table

DFA Example: 6.2
DFA Problem: Draw a DFA for the language accepting even binary number strings over the input alphabet Σ = {0,1}
Solution:
The given DFA example 6.2 provides the following
- Regular Expression = (0+1)*0
- Accepted Strings = {0, 10, 100, 110, 1110, 1010, 000, …} (binary numbers ending with ‘0’, i.e., even)
- Some Rejected Strings = {1, 11, 101, 111, 1001, 1101} (binary numbers ending with ‘1’, i.e., odd)
The required DFA diagram, for example 6.2, is given below
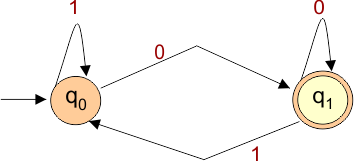
The explanation of the above DFA is given below
- States = {q0, q1}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final States = {q1}
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

If we convert the given binary language into decimal, we easily understand that the given numbers are even binary numbers
| Binary | Decimal |
|---|---|
| 0 | 0 |
| 10 | 2 |
| 100 | 4 |
| 110 | 6 |
| 1000 | 8 |
| 1010 | 10 |
| 1110 | 14 |
| 10000 | 16 |
| so on….. | — |
DFA Example: 6.3
DFA Problem: Draw a DFA for the language accepting Odd binary numbers strings over the input alphabet Σ = {0,1}
Solution:
The given DFA example 6.3 provides the following
- Regular Expression = (0+1)*1
- Accepted Strings = {1, 11, 101, 111, 1001, 1101, …} (binary numbers ending in ‘1’, i.e., odd)
- Some Rejected Strings = {ε, 0, 10, 100, 110, 1110, 1010} (binary numbers ending in ‘0’, i.e., even)
The required DFA diagram, for example 6.3, is given below

The explanation of the above DFA is given below
- States = {q0, q1}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q1
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

if we convert given binary language into decimal, we easily understant that given numbers are odd binary numbers
| Binary | Decimal |
|---|---|
| 1 | 1 |
| 11 | 3 |
| 101 | 5 |
| 111 | 7 |
| 1001 | 9 |
| 1011 | 11 |
| 1111 | 15 |
| so on …. | …. |
DFA Example: 6.4
DFA Problem: Draw a DFA for the language accepting Even or Odd binary numbers strings over input alphabets Σ = {0,1}
Solution:
The given DFA example 6.4 provides the following
- Regular Expression = (0+1)*
- Accepted Strings = {ε, 0, 1, 10, 11, 101, 1110, 1101, …} (all binary strings)
- Some Rejected Strings = Ø (None — all strings are accepted)
The required DFA diagram, for example 6.4, is given below
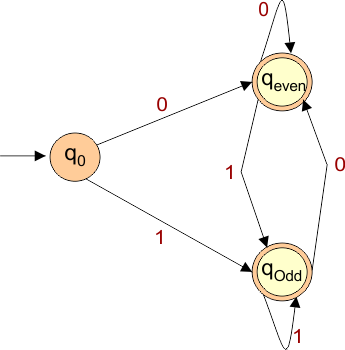
The explanation of the above DFA is given below
- States = {q0, qeven , qodd }
- Input Alphabet = {0, 1}
- Initial State = q0
- Final States = {qeven , qodd}
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 6.5
DFA Problem: Draw a DFA for Language L = {a^n b | n>= 0} over input alphabets Σ = {a,b}
Solution:
The given DFA example 6.5 provides the following
- Regular Expression = a*b
- Accepted Strings = {b, ab, aab, aaab, aaaab, …}
- Some Rejected Strings = {ε, a, aa, abb, ba, bab, bb, aaa, aaba}
The required DFA diagram, for example 6.5, is given below
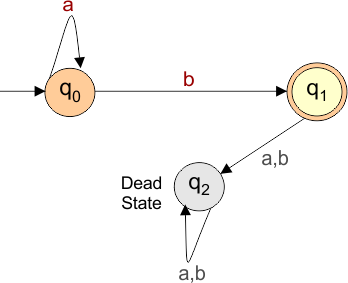
The explanation of the above DFA is given below
- States = {q0, q1, q2}
- Input Alphabet = {a, b}
- Initial State = q0
- Final State = q1
- Dead State = q2
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 6.6
DFA Problem: Draw a DFA for Language L = {0^n 1^m | m, n>= 1, (m) mode (3) = 1} over input alphabets Σ = {0,1}
Solution:
Examples in the Language L:
| String | n (0’s) | m (1’s) | m mod 3 | Accepted? |
|---|---|---|---|---|
| 01 | 1 | 1 | 1 | 1 mod 3 == 1 (yes) |
| 001 | 2 | 1 | 1 | 1 mod 3 ==1 (yes) |
| 0111 | 1 | 3 | 0 | 3 mod 3 == 1 (No) |
| 00111 | 2 | 3 | 0 | 1 mod 3 == 1 (No) |
| 001111 | 2 | 4 | 1 | 4 mod 3 == 1 (yes) |
So,
L = { 01, 001, 0001, 01, 001111, 0001111, … }
(All strings starting with 1 or more 0s, then m 1s such that m % 3 = 1)
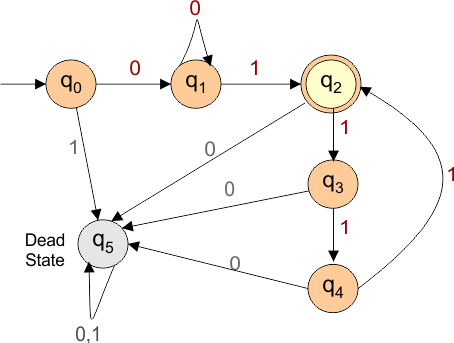
The explanation of the above DFA is given below
- States = {q0, q1,q2,q3,q4,q5}
- Input Alphabet = {0, 1}
- Initial State = q0
- Final State = q2
- Dead State = q5
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table

DFA Example: 6.7
DFA Problem: Design a DFA such that: L ={a^n b^m | n,m >= 1}
Solution:
The given DFA example 6.7 provides the following
L = {ab, aab, aaab, abbb, aabb, abbbb, …}
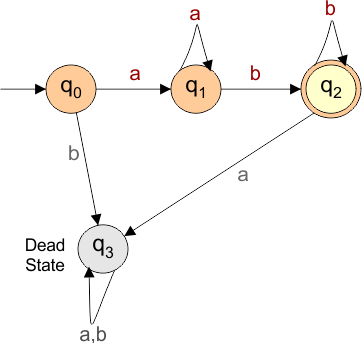
The explanation of the above DFA is given below
- States = {q0, q1, q2, q3}
- Input Alphabet = {a, b}
- Initial State = q0
- Final State = q2
- Dead state = q3
Transition Function (δ) for all input alphabets (“0,1”) is defined in the following DFA Transition Table
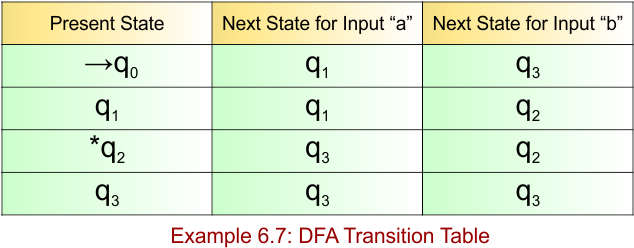
DFA Question Category 7: State and Input-based DFA Examples
Let’s discuss some state and input-based DFA examples, where we have 3, 4, and 5 different input symbols.
DFA Example: 7.1
DFA Problem: Draw a DFA that contains 4 states with the three input alphabet Σ = {a,b,c}
Solution:
The required DFA diagram, for example 7.1, is given below
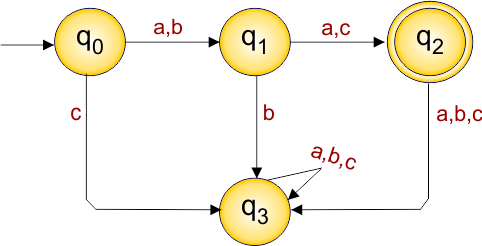
The explanation of the above DFA is given below
- States = {q0, q1,q2,q3}
- Input Alphabet = {a,b,c}
- Initial State = q0
- Final State = q2
Transition Function (δ) for all input alphabets (“a,b,c”) is defined in the following DFA Transition Table
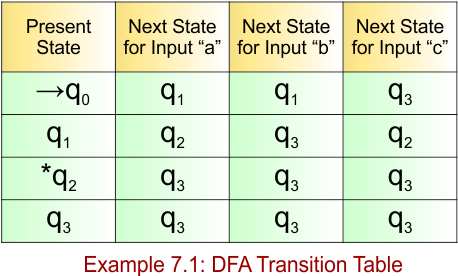
DFA Example: 7.2
DFA Problem: Draw a DFA that contains 4 states with the four input alphabet Σ = {a,b,c,d}
Solution:
The required DFA diagram, for example 7.2, is given below
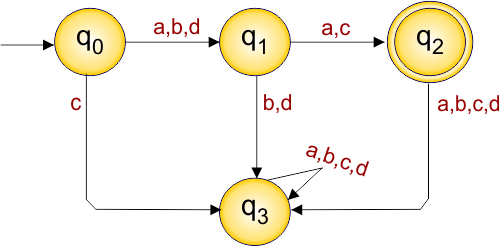
The explanation of the above DFA is given below
- States = {q0, q1,q2,q3}
- Input Alphabet = {a,b,c,d}
- Initial State = q0
- Final State = q2
Transition Function (δ) for all input alphabets (“a,b,c,d”) is defined in the following DFA Transition Table

DFA Example: 7.3
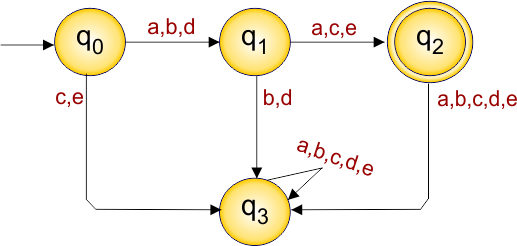
DFA Problem: Draw a DFA that contains 4 states with the five input alphabet Σ = {a,b,c,d,e}
Solution:
The required DFA diagram, for example 7.3, is given below
The explanation of the above DFA is given below
- States = {q0, q1,q2,q3}
- Input Alphabet = {a,b,c,d,e}
- Initial State = q0
- Final State = q2
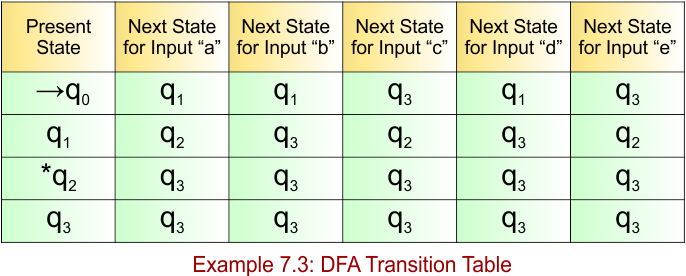
Transition Function (δ) for all input alphabets (“a,b,c,d,e”) is defined in the following DFA Transition Table