PDA Examples
Pushdown Automata (PDA) is a fundamental concept in automata theory, widely used to recognize context-free languages. In this article, we provide PDA automata examples with step-by-step solutions to understand the topic more clearly.
A list of PDA examples is shown in the following diagram
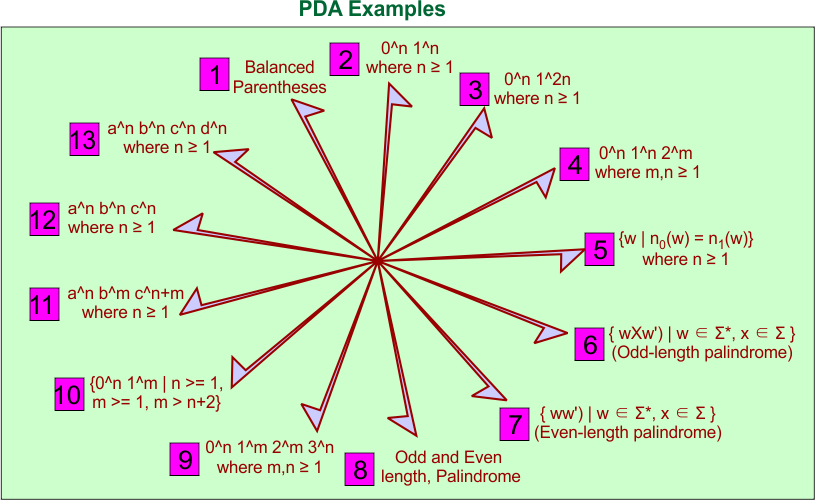
The following Symbols may be used in the PDA automata examples
|
PDA Example 01: PDA for Balanced Parentheses
Design a PDA for a language where all strings are balanced and properly nested (), {}, and [].
Examples accepted:
-
()[]{} -
{[()()]} -
[{()}([])] - so on…
Examples rejected
-
({[)]} -
([)] -
({} - so on…
Algorithm
- PUSH opening symbols:
(,{,[onto the stack. - POP when the matching closing symbol
),},]is read. - If symbols don’t match or the stack is not empty at the end, → reject.
PDA Machine Diagram
Here is a descriptive diagram to accept the string (i.e., “[{()}]“) of the given language
![PDA Example 01, for a Language of balanced paranthesis (), braces {}, and brackets []](https://cstaleem.com/wp-content/uploads/2025/06/PDA-Example-01-for-a-Language-of-balanced-paranthesis-braces-and-brackets-.png)
PDA Stack and Input Tape
Stack working with the input tape in the PDA for a Language that balances the parentheses, braces, and brackets![Input Tap and Stack for String, w = [{()}]ε](https://cstaleem.com/wp-content/uploads/2025/06/Input-Tap-and-Stack-for-String-w-ε.png)
Transition Function
PUSH for opening symbols
- δ(q0, [, Z0) → (q0,
[Z0) - δ(q0,
{, [ ) → (q0,{[) - δ(q0,
(, {) → (q0,({)
POP for Closing symbols
- δ(q0, ) , ( ) → (q1, ε)
-
δ(q0,
},{) → (q1, ε) - δ(q0, ], [ ) → (q1, ε)
Accepting condition
-
δ(q1, ε, Z0) → (q2, Z0)
The string is accepted if: the entire input is read, and the Stack has only the initial symbol (Z0), i.e., all brackets matched and popped correctly.
PDA Example 2: PDA For Language (A) = 0n1n where n ≥ 1
Let’s design the PDA for Language (A) = 0n1n where n ≥ 1
- Accepted Strings Examples: 01, 0011, 000111, 00001111, ………
- Rejected Strings Examples: 0, 1, 10, 1100, 0101, 1001, …….
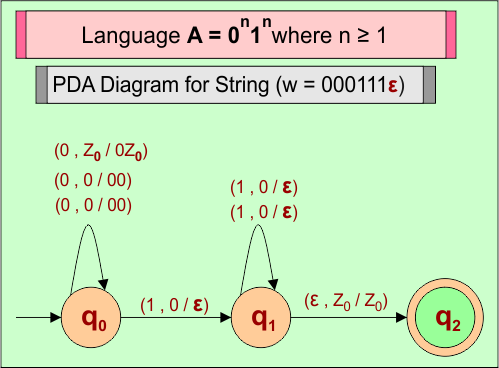
Consider a string (w =”000111ε”) from Language (A) = 0n1n where n ≥ 1 to design its PDA.
Algorithm
Here is the algorithm to accept all strings (i.e., w =”000111ε”) from Language (A) = 0n1n where n ≥ 1
- For each input “0”, PUSH “0” into stack.
- For each input “1”, POP “0” from stack.
- For the last input “ε”, the Stack remains unchanged, and string (“000111ε”) is accepted.
PDA Machine Diagram
Here is a descriptive diagram to accept the string (“000111ε”) of Language (A) = 0n1n where n ≥ 1
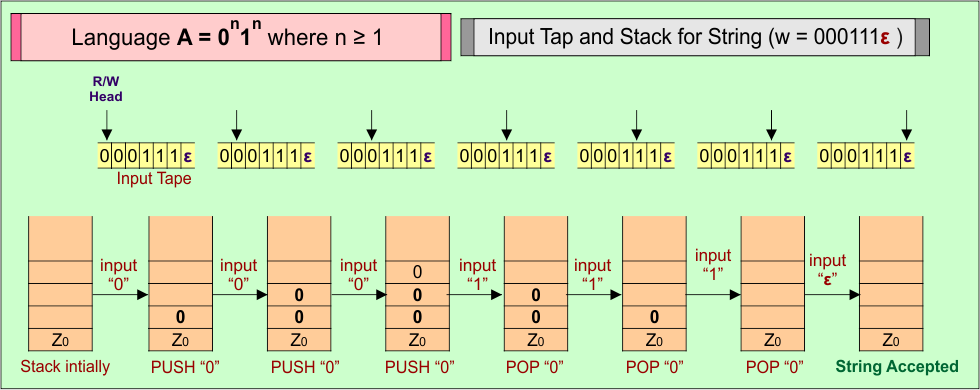
PDA Stack and Input Tape
Stack working with the input tape in the PDA for Language (A) = 0n1n where n ≥ 1
PDA Transition Functions
Here is the descriptive diagram to represent the transition functions to accept the string (“000111ε”) of Language (A) = 0n1n where n ≥ 1

PDA Example 3: PDA For Language (A) = 0n12n where n ≥ 1
Let’s design the PDA for Language (A) = 0n12n where n ≥ 1
- Accepted Strings Examples: 011, 001111, 000111111, 000011111111 ……….
- Rejected Strings Examples: 01, 100, 110000, 101, 001, ……..
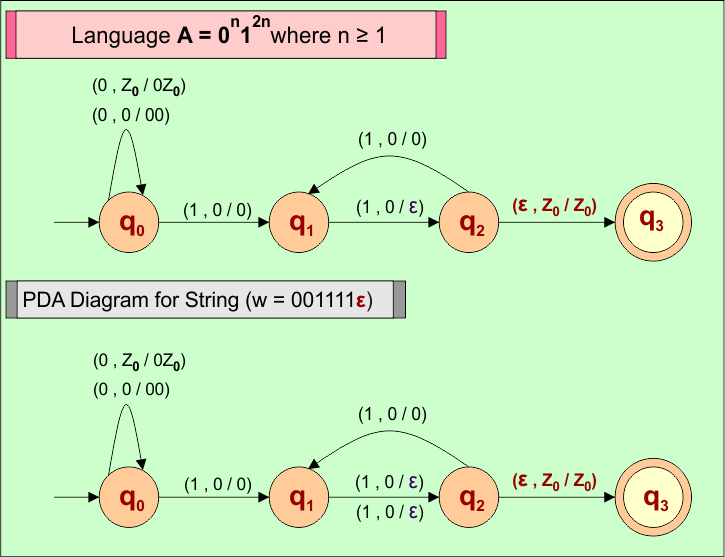
Consider a string (w =”001111ε”) from Language (A) = 0n12n where n ≥ 1 to design its PDA.
Algorithm
Here is the algorithm to accept all strings (i.e., w =”001111ε”) from Language (A) = 0n12n where n ≥ 1
- For each input “0”, PUSH “0” into stack.
- For each input “1”, for every 2
1s, one0is popped- Ignore the first
1in every pair - POP one
0for every second1
- Ignore the first
- For the last input “ε”, the Stack remains unchanged, and string (“001111ε”) is accepted.
PDA Machine Diagram
Here is a descriptive diagram to accept the string (“001111ε”) of Language (A) = 0n12n where n ≥ 1
PDA Stack and Input Tape
Stack working with the input tape in the PDA for Language (A) = 0n12n where n ≥ 1
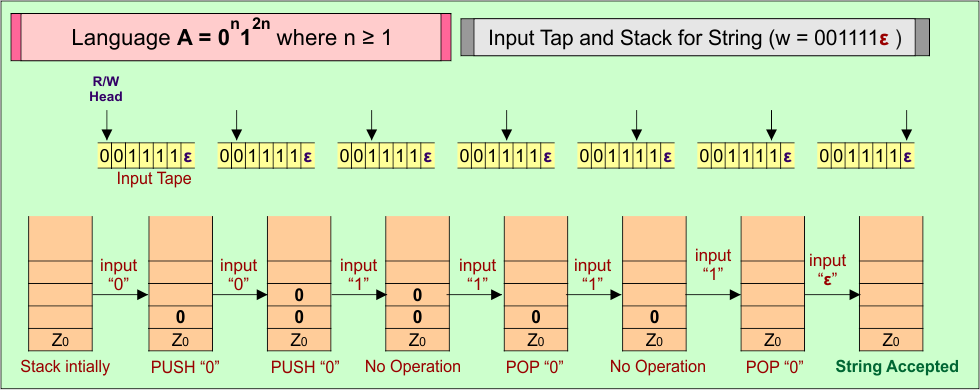
PDA Transition Functions
Here is the descriptive diagram to represent the transition functions to accept the string (“001111ε”) of Language (A) = 0n12n where n ≥ 1

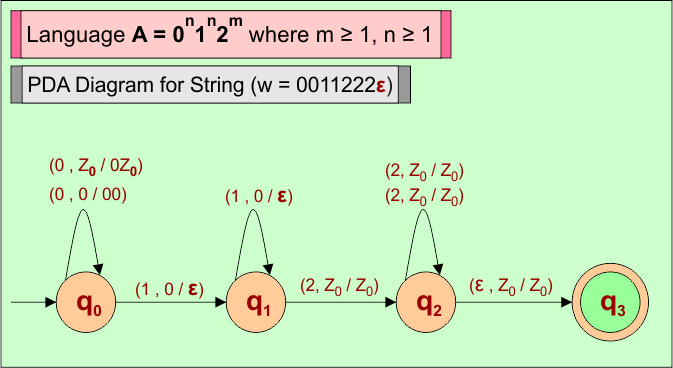
PDA Example 4: PDA For Language (A) = 0n1n2m where m ≥ 1, n ≥ 1
Let’s design the PDA for Language (A) = 0n1n2m where m ≥ 1, n ≥ 1
- Accepted Strings Examples: 012, 00112, 0011222, 0001112222, ……….
- Rejected Strings Examples: 0012, 001112, 0001222, 001112, ……………….
Consider a string (w =”0011222ε”) from Language A = 0n1n2m where m ≥ 1, n ≥ 1 to design its PDA.
Algorithm
Here is the algorithm to accept all strings (i.e., w =”0011222ε”) from Language A = 0n1n2m where m ≥ 1, n ≥ 1
- For each input “0”, PUSH “0” in stack.
- For each input “1”, POP “0” from stack.
- For each input “2”, the Stack remains unchanged
- For the last input “ε”, the Stack remains unchanged, string (“0011222ε”) is accepted.
PDA Machine Diagram
Here is a descriptive diagram to accept the string (“0011222ε”) of Language (A) = 0n1n2m where m ≥ 1, n ≥ 1
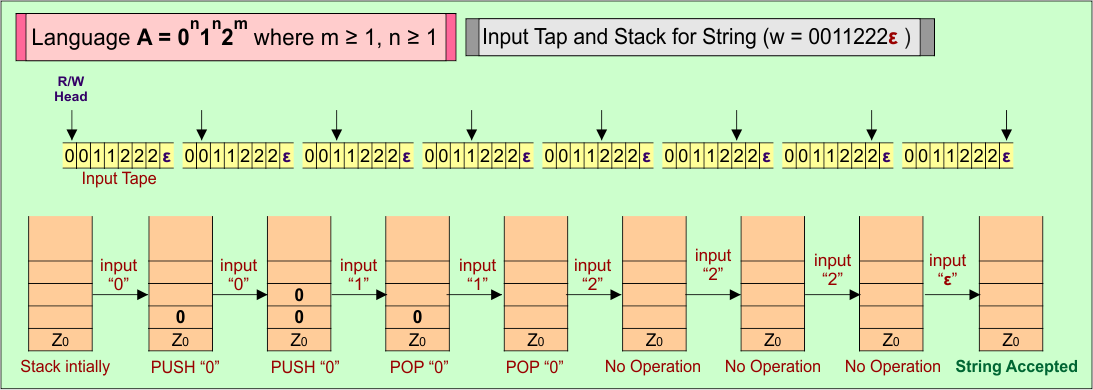
PDA Stack and Input Tape
Stack working with the input tape in the PDA for string (“0011222ε”) of Language (A) = 0n1n2m where m ≥ 1, n ≥ 1
PDA Transition Functions
Here is the descriptive diagram to represent the transition functions to accept the string (“0011222ε”) of Language (A) = 0n1n2m where m ≥ 1, n ≥ 1

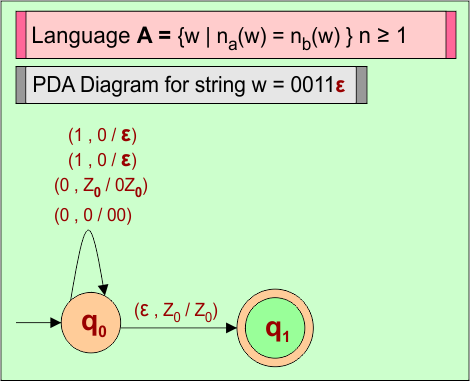
PDA Example 5: PDA For Language (A) = {w | n0(w) = n1(w)} where n ≥ 1
Problem Explained: (Number of 0’s must equal to number of “1’s” in string(“w”) where {w = w | n0(w) = n1(w)}.
Let’s design the PDA for Language (A) = {w | n0(w) = n1(w)}.
- Accepted Strings Examples: 01, 0011, 0101, 001101, 000111, 00011101, ……….
- Rejected Strings Examples: 0, 1, 001, 100, 010100, 00011100, 010001111, ……………….
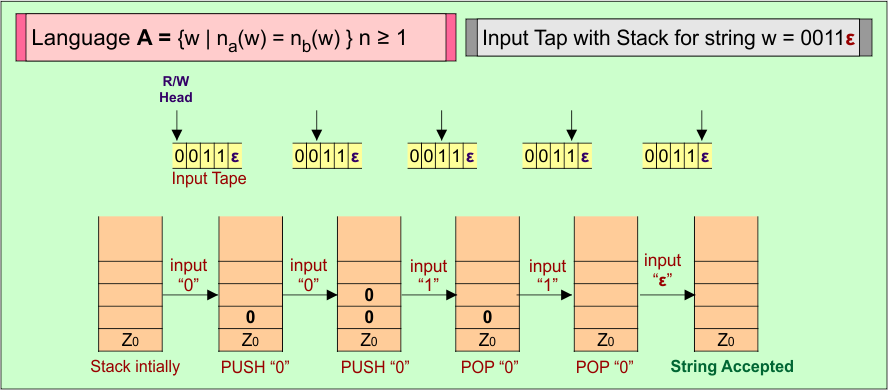
Consider a string (w =”0011ε”) from Language A = {w | n0(w) = n1(w)} where n ≥ 1 to design its PDA.
Algorithm
Here is the algorithm to accept all strings (i.e., w =”0011ε”) from Language A = {w | n0(w) = n1(w)} where n ≥ 1
- For each input “0”, PUSH “0” in stack.
- For each input “1”, POP “0” from stack.
- For the last input “ε”, the Stack remains unchanged, string (“0011ε”) is accepted.
PDA Machine Diagram
Here is a descriptive diagram to accept the string (“0011ε”) of Language (A) = {w | n0(w) = n1(w)} where n ≥ 1.
PDA Stack and Input Tape
Stack working with the input tape in the PDA for Language (A) = {w | n0(w) = n1(w)} n ≥ 1
PDA Transition Functions
Here is the descriptive diagram to represent the transition functions to accept the string (“0011ε”) of Language (A) = {w | n0(w) = n1(w)} n ≥ 1

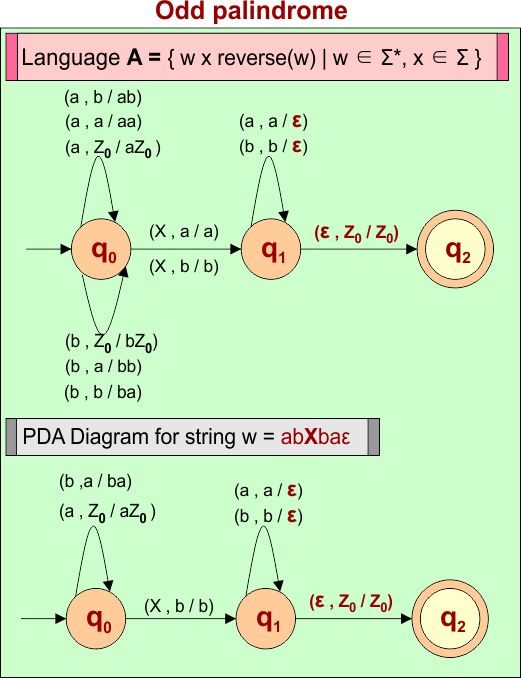
PDA Example 6: PDA For Language A = { wXw’) | w ∈ Σ*, x ∈ Σ }
Let’s design the PDA for Language A = { wXw’) | w ∈ Σ*, X ∈ Σ }. This problem is also called an Odd-length palindrome
- Accepted Strings Examples: aXa, abXba, abbXbba, aaaabXbaaaa,………
- Rejected Strings Examples: ab, abaa,…..
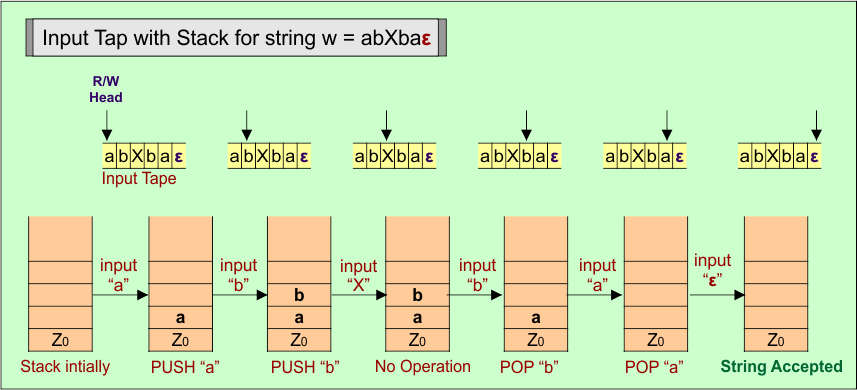
Consider a string (w =”abXbaε”) from Language A = { wXw’) | w ∈ Σ*, x ∈ Σ } to design its PDA.
Algorithm
Here is the algorithm to accept all strings (i.e., w =”abXbaε”) from Language A = { wXw’) | w ∈ Σ*, x ∈ Σ }.
Start of the string
- For each input “a”, PUSH “a” into the stack.
- For each input “b”, PUSH “b” into the stack.
After reaching the Middle of the string by getting (“X”), the stack remains unchanged
- For each input “b”, POP “b” from the stack.
- For each input “a”, POP “a” from the stack.
For the last input “ε”, the Stack remains unchanged, and string (“abXbaε”) is accepted.
PDA Machine Diagram
Here is a descriptive diagram to accept all strings of even length palindromes and a specific string (i.e., “abbaε”)
PDA Stack and Input Tape
Stack working with the input tape in the PDA for odd-length palindrome, string example is “abXbaε”
PDA Transition Functions
Here is the descriptive diagram to represent the transition functions to accept the string (“abXbaε”) of odd length palindrome

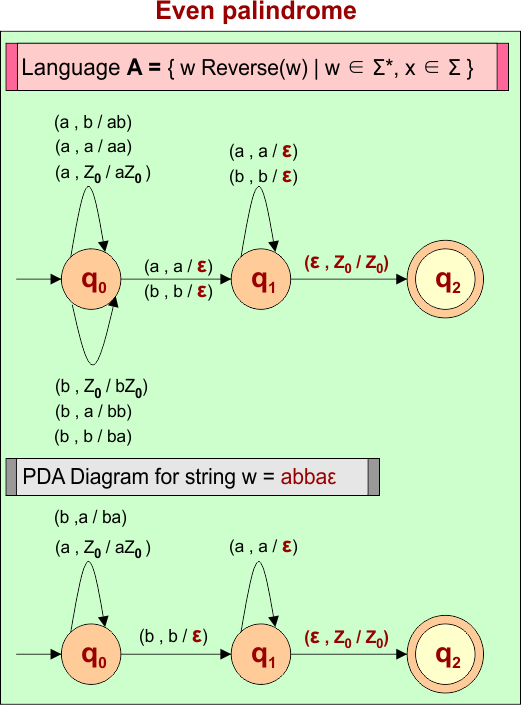
PDA Example 7: PDA For Language A = { ww’) | w ∈ Σ*, x ∈ Σ }
Let’s design the PDA for Language A = { ww’) | w ∈ Σ*, x ∈ Σ }. This problem is also called an even-length palindrome
- Accepted Strings Examples: aa, abba, abbbba, aaaabbaaaa,………
- Rejected Strings Examples: ab, abaa,…..
Consider a string (w =”abbaε”) from Language A = { ww’) | w ∈ Σ*, x ∈ Σ } to design its PDA.
Algorithm
Here is the algorithm to accept all strings (i.e., w =”abbaε”) from Language A = { ww’) | w ∈ Σ*, x ∈ Σ }.
Start of the string
- For each input “a”, PUSH “a” into the stack.
- For each input “b”, PUSH “b” into the stack.
After reaching the Middle of the string
- For each input “b”, POP “b” from the stack.
- For each input “a”, POP “a” from the stack.
For the last input “ε”, the Stack remains unchanged, and string (“abbaε”) is accepted.
Note: Finding center is an other question in even-length palindrome
PDA Machine Diagram
Here is a descriptive diagram to accept all strings of even length palindromes and a specific string (i.e., “abbaε”)
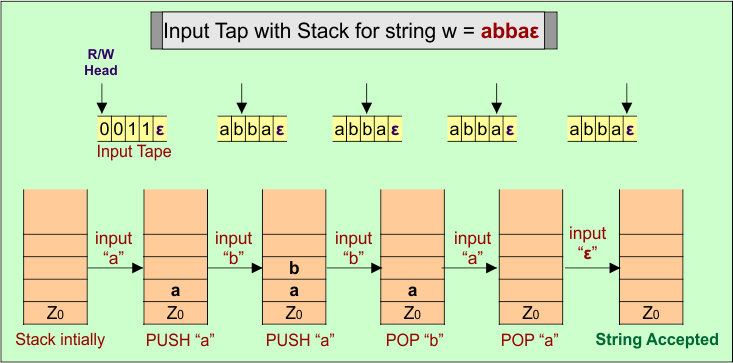
PDA Stack and Input Tape
Stack working with the input tape in the PDA for an even-length palindrome.
PDA Transition Functions
Here is the descriptive diagram to represent the transition functions to accept the string (“abbaε”) of an even-length palindrome.

PDA Example 8: PDA For Odd and Even, Palindrome
Accepted Strings Examples for Odd and Even, Palindrome are given below
- Length of string is even (e.g., 2, 4, 6…), examples:
aa,abba,noon,........ - Length of string is odd (e.g., 1, 3, 5…), examples:
a,aba,madam,……..
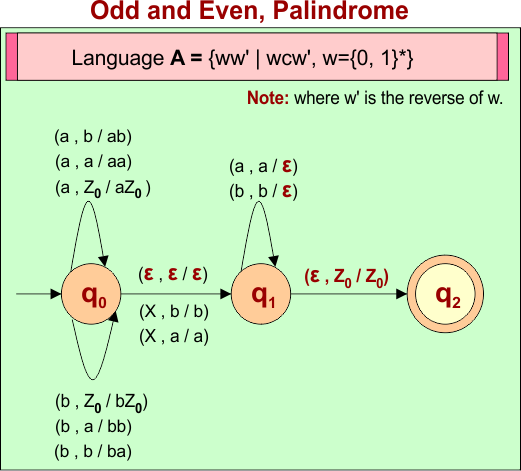
PDA Machine Diagram
Here is a descriptive diagram to accept all strings for Odd and Even length Palindrome
PDA Automata Example 9: PDA For Language A = 0n1m2m3n where n ≥ 1, m ≥ 1
Problem Explained:
Let’s design the PDA for Language (A) = 0n1m2m3n where n ≥ 1, m ≥ 1
- Accepted Strings Examples:
- Rejected Strings Examples:
Consider a string (w =”011223ε”) from Language A = 0n1m2m3n where n ≥ 1, m ≥ 1 to design its PDA.
Algorithm
Here is the algorithm to accept all strings (i.e., w =”011223ε”) from Language A = 0n1m2m3n where n ≥ 1, m ≥ 1
- For each input “0”, PUSH “0” into the stack.
- For each input “1”, PUSH “1” into the stack.
- For each input “2”, POP “1” from the stack.
- For each input “3”, POP “0” from the stack.
- For the last input “ε”, the Stack remains unchanged, string (i.e., “011223ε”) is accepted.
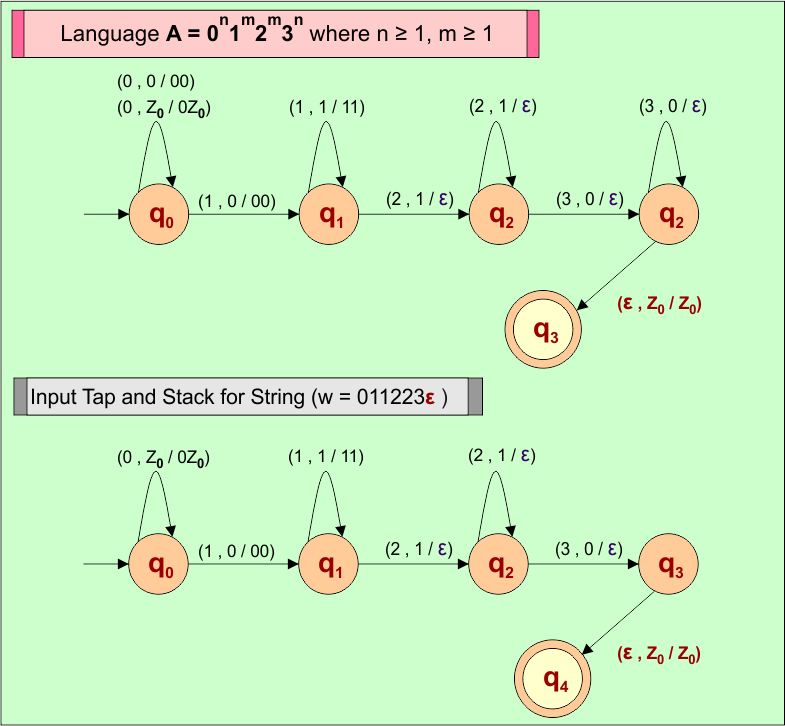
PDA Machine Diagram
Here is a descriptive diagram to accept the string (“011223ε”) of Language (A) = 0n1m2m3n where n ≥ 1, m ≥ 1.
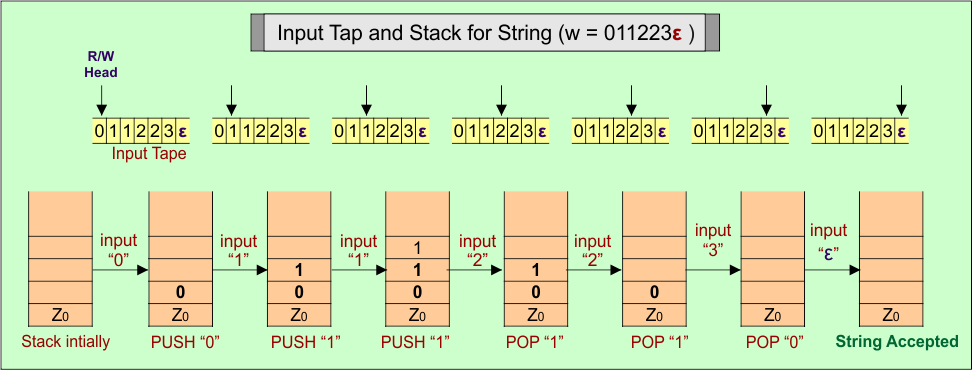
PDA Stack and Input Tape
Stack working with the input tape in the PDA for the string (“011223ε”) of Language (A) = 0n1m2m3n where n ≥ 1, m ≥ 1
PDA Transition Functions
Here is the descriptive diagram to represent the transition functions to accept the string (“011223ε”) of Language (A) = 0n1m2m3n where n ≥ 1, m ≥ 1

PDA Example 10: PDA For Language A = {0^n 1^m | n >= 1, m >= 1, m > n+2}
Let’s design the PDA for Language (A) = {0^n 1^m | n >= 1, m >= 1, m > n+2}
- Accepted Strings Examples: 0111, 001111, 00011111, 0000111111, ……….
- Rejected Strings Examples: 01, 0011, 1110, ……………….
Consider a string (w =”011ε”) from Language (A) = {0^n 1^m | n >= 1, m >= 1, m > n+2} to design its PDA.
Algorithm
| PUSH 0 with each 0 pop 0 with each 1 add two extra “1” |
Here is the algorithm to accept all strings (i.e., w =”0011ε”) from Language A = {0^n 1^m | n >= 1, m >= 1, m > n+2}
- For each input “0”, PUSH “0” in stack.
- For each input “1”, POP “0” from stack.
- After, POP all 0’s,
- For both input “1”, “1”, the stack remains unchanged
- For the last input “ε”, the Stack remains unchanged, string (“0111ε”) is accepted.
PDA Machine Diagram
Here is a descriptive diagram to accept the string (“0111ε”) of Language (A) = {0^n 1^m | n >= 1, m >= 1, m > n+2}

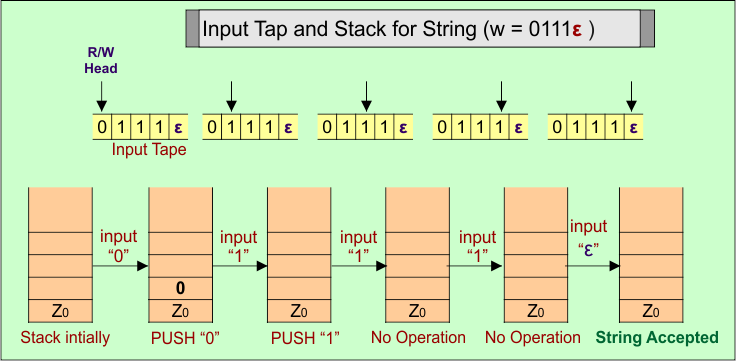
PDA Stack and Input Tape
Stack working with the input tape in the PDA for the string (“0111ε”) of Language (A) = {0^n 1^m | n >= 1, m >= 1, m > n+2}
PDA Transition Functions
Here is the descriptive diagram to represent the transition functions to accept the string (“0111ε”) of Language (A) = {0^n 1^m | n >= 1, m >= 1, m > n+2}

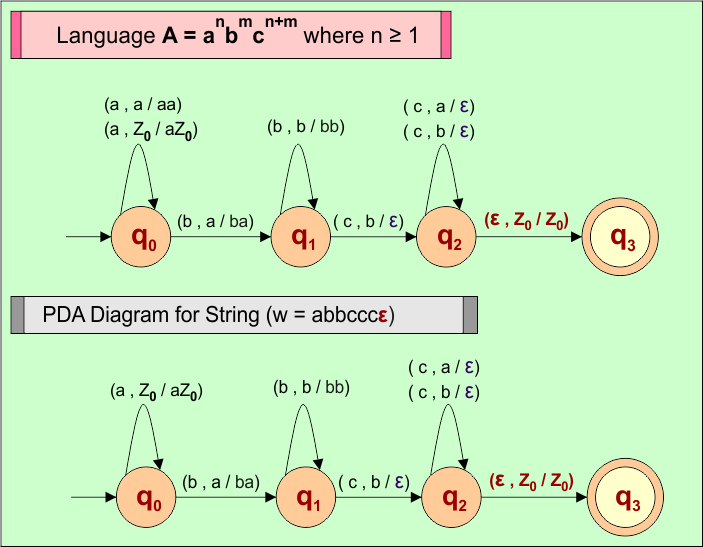
PDA Example 11: PDA For Language A = anbmcn+m where n ≥ 1
Let’s design the PDA for Language (A) = anbmcn+m where n ≥ 1
- Accepted Strings Examples: abcc, aabccc, aaabcccc, abbbcccc,……
- Rejected Strings Examples: abc, abccc, abbc,……..
Consider a string (w =”abbcccε”) from Language A = anbmcn+m where n ≥ 1 to design its PDA.
Algorithm
Here is the algorithm to accept all strings (i.e., w =”abbcccε”) from Language A = anbmcn+m where n ≥ 1
- For each input “a”, PUSH “a” in stack.
- For each input “b”, PUSH “b” in stack.
- For each input “c”, POP (“a” or “b”) from stack.
- For the last input “ε”, the Stack remains unchanged, string (i.e. “abbcccε”) is accepted.
PDA Machine Diagram
Here is a descriptive diagram to accept the string (“abbcccε”) of Language (A) = anbmcn+m where n ≥ 1.
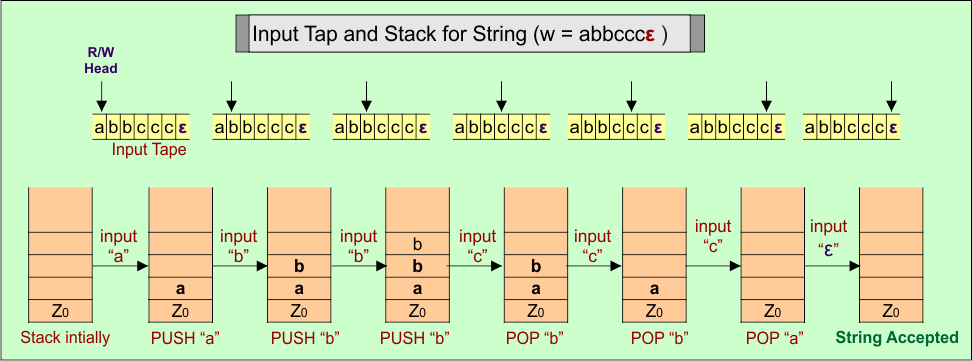
PDA Stack and Input Tape
Stack working with the input tape in the PDA for Language (A) = anbmcn+m where n ≥ 1
PDA Transition Functions
Here is the descriptive diagram to represent the transition functions to accept the string (“abbcccε”) of Language (A) = anbmcn+m where n ≥ 1.

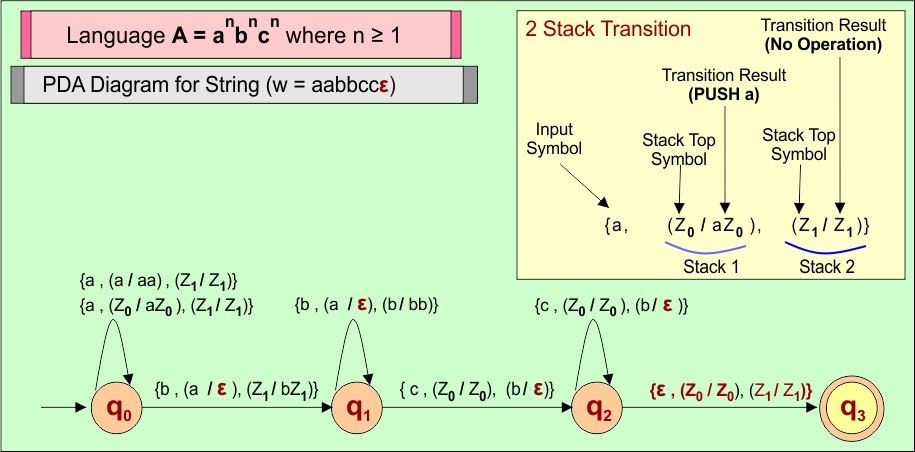
PDA Example 12: PDA For Language A = anbncn where n ≥ 1
Let’s design the PDA for Language (A) = anbncn where n ≥ 1
| Important: Language (A) = anbncn, where n ≥ 1 is not a regular language. If we want to design a PDA for this type of language, then we require at least two stacks. |
Accepted Strings Examples
| n | String | Explanation |
|---|---|---|
| 1 | abc |
1 a, 1 b, 1 c |
| 2 | aabbcc |
2 a’s, 2 b’s, 2 c’s |
| 3 | aaabbbccc |
3 a’s, 3 b’s, 3 c’s |
| 4 | aaaabbbbcccc |
4 a’s, 4 b’s, 4 c’s |
| String | Reason for Rejection |
|---|---|
aabbc |
Unequal count of characters |
abcc |
b and c counts don’t match a |
aabbbccc |
2 a’s, 3 b’s, 3 c’s → not equal |
abcabc |
Wrong order / repeated pattern |
cba |
Wrong order (should be a→b→c) |
Consider a string (w =”aabbccε”) from Language A = anbncn where n ≥ 1 to design its PDA.
Algorithm
Here is the algorithm to accept all strings from Language A = anbncn where n ≥ 1
- For each input a: PUSH a in Stack 1, and Stack 2 is empty
- For each input b: POP a from Stack 1, PUSH b in Stack 2
- For each input c: Stack 1 nothing, POP b from Stack 2
PDA Machine Diagram
Here is a descriptive diagram to accept the string (i.e. “aabbccε”) of Language (A) = anbncn where n ≥ 1
PDA Stack and Input Tape
Stack working with the input tape in the PDA for the string (i.e. “aabbccε”) of Language (A) = anbncn where n ≥ 1
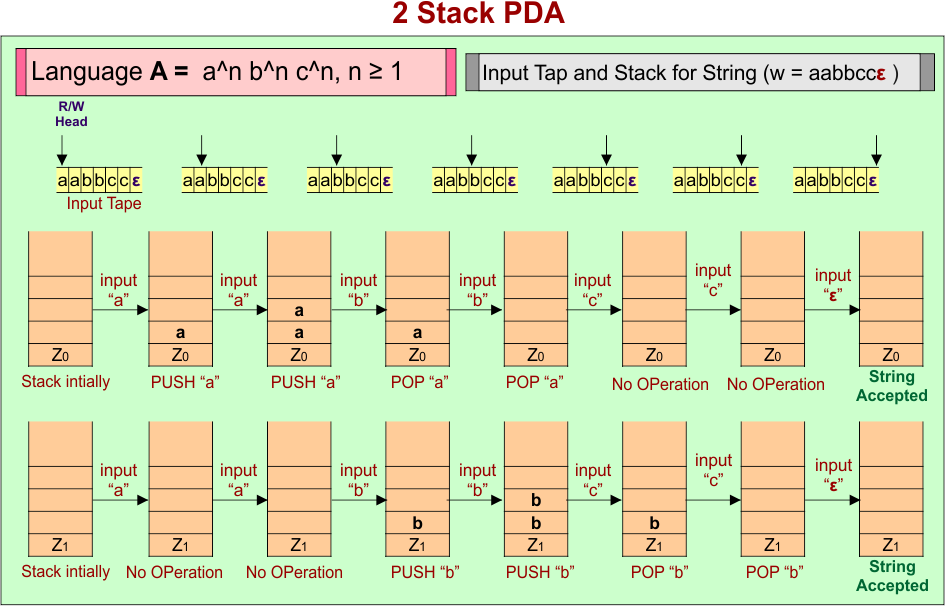
PDA Example 13: PDA For Language A = anbncndn where n ≥ 1
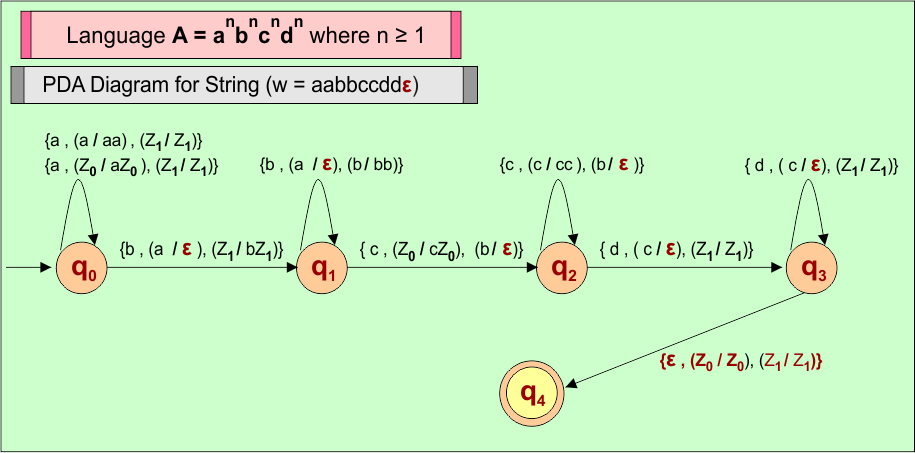
Let’s design the PDA for Language (A) = anbncndn where n ≥ 1.
| Important: Language (A) = anbncndn, where n ≥ 1 is not a regular language. If we want to design a PDA for this type of language, then we require at least two stacks. |
Accepted Strings (n = 1 to 5)
abcdaabbccddaaabbbcccdddaaaabbbbccccddddaaaaabbbbbcccccddddd
Rejected Strings (Invalid examples with reasons)
abcdd– extradaabbcc– missingdaabbbcccddd– unequal number ofaandbabdc– incorrect orderabcdabcd– pattern repetition not allowed
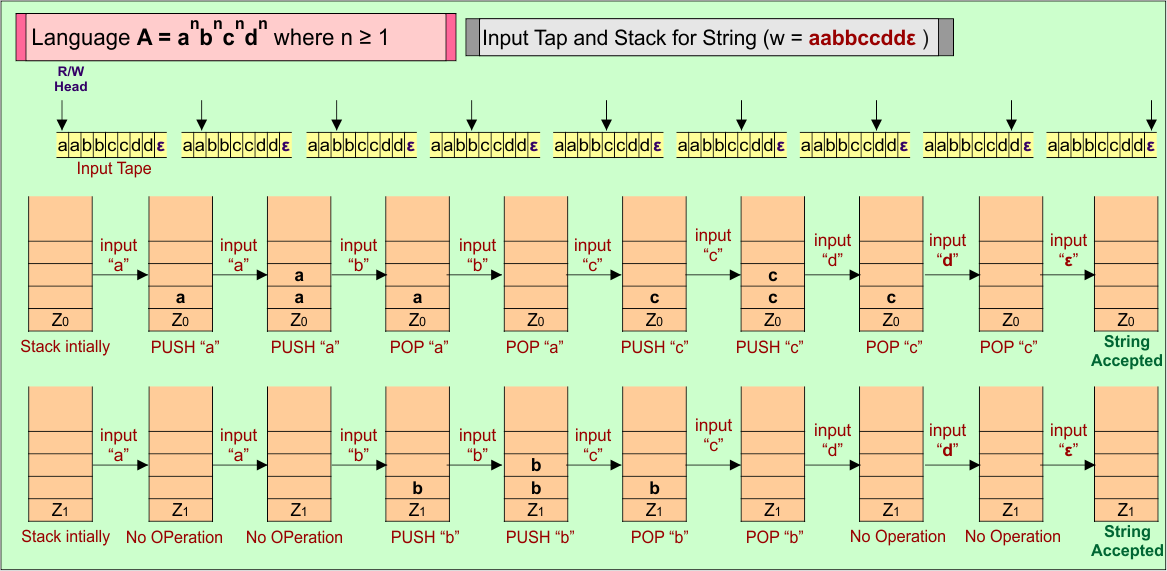
Consider a string (w =”aabbccddε”) from Language (A) = anbncndn where n ≥ 1 to design its PDA.
Algorithm
Here is the algorithm to accept all strings from Language (A) = anbncndn where n ≥ 1
- For each input a: PUSH a in Stack 1, and Stack 2 remains unchanged
- For each input b: POP a from Stack 1, PUSH b in Stack 2
- For each input c: PUSH c in Stack 1, POP b from Stack 2
- For each input d: POP c from Stack 1, Stack 2 remains unchanged
PDA Machine Diagram
Here is a descriptive diagram to accept the string (“aabbccddε”) of Language (A) = anbncndn where n ≥ 1
PDA Stack and Input Tape
Stack working with the input tape in the PDA for the string (“aabbccddε”) of Language (A) = anbncndn where n ≥ 1
1-Stack PDA vs 2-Stack PDA
1-Stack PDA
- A 1-stack PDA uses a single stack for memory.
- It accepts Context-Free Languages (CFLs).
- Transition function for a 1-stack PDA is δ: (Q × Σ ∪ {ε} × Γ) → (Q × Γ*)
- Example: Language
{ a^n b^n | n ≥ 0 }is accepted by 1-stack PDA. - It cannot accept languages like
{ a^n b^n c^n }. - CFLs are exactly the class of languages accepted by 1-stack non-deterministic PDAs.
2-Stack PDA
- A 2-stack PDA has two stacks for memory.
- It is equivalent in power to a Turing Machine.
- It can accept recursively enumerable languages.
- Transition function for a 1-stack PDA is δ: (Q × Σ ∪ {ε} × Γ × Γ) → (Q × Γ* × Γ*)
- Example:
{ a^n b^n c^n | n ≥ 0 }is accepted by 2 – stack PDA. - Thus, 1-stack PDA ⊂ 2-stack PDA in terms of language acceptance.














![Transition Function for string w = [{()}]ε](https://cstaleem.com/wp-content/uploads/2025/06/Transition-Function-for-string-w-ε.png)