Transition Table and Diagrams
A transition table represents the transitions for each state and input symbol in TOC (theory of computations). It plays an important role in defining how an automata machine moves from one state to another based on input symbols.
The transition table contains the following
- Rows: It mostly represents the current state of the automata machine.
- Columns: These represent the input symbols from the alphabet.
- Cells: Each cell in the table specifies the next state. In the case of NFA, more than one state can be found in each cell.
Transition tabular form provides a clear, unambiguous representation of the automata operations, by facilitating analysis and understanding of its behavior.
Components of a Transition Table
Each transition table contains the states, input alphabets, and transitions. Let’s explain these components
- States: All the states in the TOC are listed, usually in the rows. This includes the start state and one or many final states.
- Alphabet: The set of input symbols that the automata machine can read, mostly listed in the columns.
- Transitions: it is defined for each pair of states and input symbol, which tells the next state of the automata machine.
Important: For a DFA, there is exactly one next state for each state-symbol pair. But in NFA, there can be zero, one, or multiple next states for each state-symbol pair.
Transition Table Examples in TOC
A transition table can be used to represent the DFA or NFA diagrams, Let explain both of these behavior in TOC.
DFA Transition Diagram and Table
In a DFA, for every state and input symbol, there is exactly one transition to the next state. This deterministic nature simplifies the transition table since each cell will contain exactly one state. Let’s explain with an example
Example: Draw a DFA that Recognizing Strings Ending in “01”
Let’s define a DFA transition diagram that accepts all strings ending in the substring “01” over the alphabet {0, 1}.
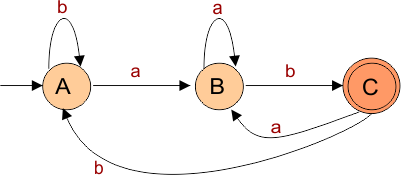
- States: A (start), B (intermediate), and C is the final state.
- Input Alphabet: {0, 1}
Following is the Transition Table in the TOC
| State | 0 | 1 |
| ->A | B | A |
| B | B | C |
| {C} | B | A |
Explanation:
When at start state A,
- For input “0”, the transition goes to state “B”
- For input “1”, the transition remains in the same state “A”
When at state B,
- For input “0”, the transition remains in the same state “B”
- For input “1”, the transition goes to next state “C” which is final.
When at state C,
- For input “0”, the transition goes to state “B”
- For input “1”, the transition goes to state “A”.
Note: ->A denotes the start state, {C} denotes an accept state.
NFA Transition Diagram and Table
NFAs can transition to any number of states (including zero) for a given state and input symbol. This non-determinism is reflected in the transition table where each cell may contain zero, one, or multiple states.
Example: Draw an NFA where the second last bit is 1 over input alphabets are ∑ = {0, 1}.
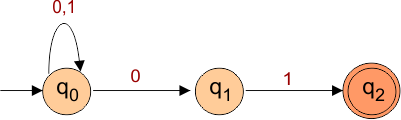
- States: q0, q1, and q2. Where q0 is starting and q2 is the final state
- Alphabet: {0, 1}
Transition Table:
| States | 0 | 1 |
| -> q0 | q0 | q0,q1 |
| q1 | q2 | q2 |
| {q2} | – | – |
Explanation:
When at start state q0,
- For input “1”, the transition goes to states q0 and q1.
- For input “0”, the transition remains in the same state as “q0”
When at state q1,
- For input “0” and “1”, the transition goes to state “q1”
When at state q2,
- No transitions found
Epsilon (ε) NFA Transition Table and Diagram
In ε-NFA is an extension of NFA. Epsilon (ε) transitions occur without consuming any input symbol. It adds another layer of complexity.
Example: Draw an ε-NFA machine that accepts the string “a, b, or c”.
The required ε-NFA is given below
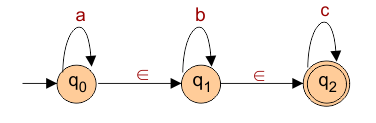
- States: q0, q1, and q2. Where q0 is starting and q2 is the final state
- Alphabet: {a, b, c}
Transition in Table:
| States | a | b | c | Epsilon (ε) |
| -> q0 | q0 | — | – | q1 |
| q1 | — | q1 | – | q2 |
| {q2} | – | – | q2 | – |
FAQ for Transition Table in TOC
Let’s discuss the most important question related to the transition table in TOC.
Question 01: What is a transition table in the context of finite automata?
A transition table helps to understand how the automata machine moves from one state to another, based on the current state and the input symbol it reads. In the case of DFA transition table, a clear, one-to-one mapping for the state-input pair exists but in the case of NFA multiple or no next states can be found for the state-input pair.
Question 02: How does a transition table differ for DFA and NFA?
DFA Transition Tables are designed in such a way that each entry in the table uniquely determines a single next state for a given state and input symbol. This reflects the deterministic nature of DFAs.
NFA Transition Tables can list multiple next states for a single state-input pair, reflecting the non-deterministic nature of NFAs. For a given state and input symbol, an NFA can transition to any number of new states, including zero or more. NFA Transition Tables may also include ε-transitions, which are instances where the automaton moves to a new state without consuming any input.
Question 03: What are ε-transitions, and how are they represented in transition tables?
ε-Transitions are special transitions in NFAs where the automata machine moves from one state to another without consuming any input symbol. In transition tables, ε-transitions are typically represented in a separate column labeled ε.
Question 04: Can transition tables represent infinite languages?
Yes, Finite automata transition tables can represent finite and infinite languages. The automaton itself has a finite number of states and transitions, which are represented in the transition table. However, it can recognize languages with infinitely many strings by cycling through states.
Question 05: How Do We Make Transition Tables for Really Complex Machines?
When dealing with complex machines that have a lot of states or inputs, making a transition table might seem complex. Follow the following method
- List all states: note down all possible states.
- List all inputs: These are the different “input symbols” that can change the machine’s state.
- Fill in the table: For each state and each input, decide what the new state will be. This is like answering, “If I’m here and this happens, where do I go next?”
Question 06: Can Transition Tables Work with Languages That Aren’t Regular?
Transition tables are an effective approach for handling regular languages. However, when dealing with non-regular languages, which require more information than a finite automaton to handle, transition tables become short. For such cases, we require more complex machines like pushdown automata or Turing machines, which have their own methods for tracking more complex patterns.













