Turing Machine Examples
Before understanding the turning machine examples, let’s see the 7-tuples (Q, T, B, ∑, δ, q0, F) which show the mechanism of the Turning machine. Following are the 7-Tuples of the Turing machine.
- Q contains a finite set of states.
- T is the input tape that holds the Input and Special symbols. So, Both input and Special symbols are subsets of input tape T.
- B is a Special symbol, also called a Blank symbol (every cell is filled with a special symbol except the input alphabet initially)
- ∑ is the input symbols (input tape holds initial input alphabet)
- δ is a transition function is Q × T → Q × T × {L,R}. At any state (Q) when the
- If the input tape symbol (T) is applied, it will move to a new state, update the tape symbol (may or may not change), and move the head pointer to either right or left.
- q0 is the initial state.
- F is the set of final states. It is considered accepted when the input string reaches a state of F.
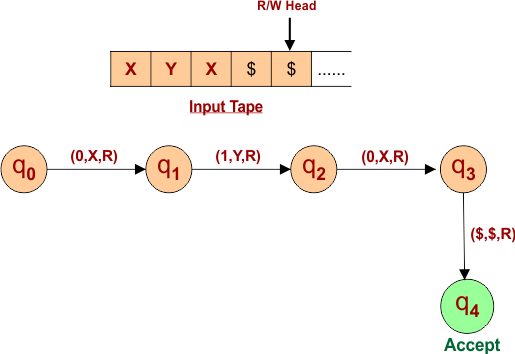
Example 01: Turing Machine for Language L= “010”
Let us construct a Turing machine for simple language L= “010”. The Input tape for language “010” will become as follows.
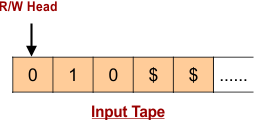
Special symbols are inserted after entering the language “010” into the input tape. This language is considered valid upon the arrival of the first special symbol.
Consider,
- Q = {q0,q1,q2,q3} where q0 is initial state.
- T = {0,1, X, Y,$} where $ represents blank.
- ∑ = {0,1}
- F = {q3}
| Important: Symbols “X and Y” In input Tape are used to Update values of Sigma input ∑ (0,1). It is just identification that tells that the input symbols are read successfully.
(i.e., when reading Sigma input “0”, it should update with “X” in the input tap, and “1” should use “Y”). |
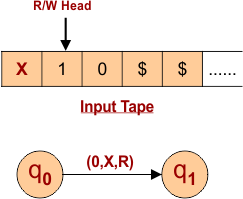
“0” for First Input Symol
- Transition goes to state (q1) from initial state (q0)
- The input tape’s first symbol, “0”, is updated to “X”.
- Read/Write Head Goes to One Position Right.
“1” for Second Input
- Transition goes to state (q2) from state (q1)
- The input tape’s second symbol, “1”, is updated to “Y”.
- Read/Write Head Goes to One Position Right.

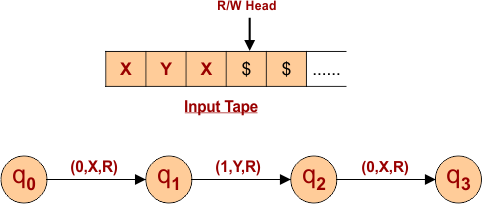
“0” for Third Input
- Transition goes to state (q3) from state (q2)
- The third symbol on the input tape, which is currently “0,” is being changed to “X.”
- Read/Write Head Goes to One Position Right.
“$” for First Special Symbol
- The transition goes to state (q4) from state (q3), which is the accepting state.
- The special symbol “$” on the input tape remains unchanged.
- Read/Write Head Goes to One Position Right.
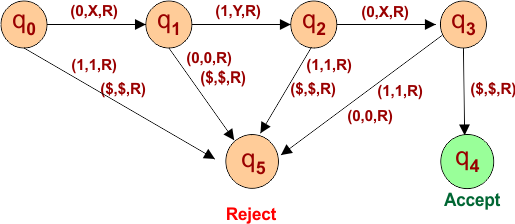
Other than the “010” language, all languages are rejected. All possible paths for each input (0,1 and $) at each state are given below.
Example 02: Turing machine for 0^N1^N
Design a Turing Machine that recognizes the language L = 0^N1^N where N>0
Solution
Given language (L = 0N1N) will generate an equal number of 0s and 1s. Consider the following input tap that contains L=000111.

Algorithm for language 0^N1^N (L = 0N1N)
Following is the algorithm for the above language in the Turing Machine.
- Step 01: Change 0 to X
- Step 02: Move Right to the First 1. If you do not find symbol (1), reject the language.
- Step 03: Change 1 to Y
- Step 04: Move Left to Leftmost 0
- Step 05: Repeat Steps number 01 to 04 until no more 0 and 1 remain in the input tape.
Let’s construct a Turing Machine for a string 000111 of a given language.
According to Step 01, For the first input (0)
- The transition goes from the initial state (q0) to state (q1).
- The system converts the input tape’s first symbol, 0, to X.
- Read/Write head moves one step to the right side.

According to steps 2 and 3
R/W Head moves to the right To update the first symbol (1) on the right side of the input tape,
- Transition goes from state (q1) to state (q2).
- The system converts the input tape symbol,1, to Y.
- R/W Head Move one Position Left to update the Leftmost 0 in the next.
The following diagram shows that, at state q1, input 0 will keep the transition in the same state.

According To steps 4 and 01
R/W Head moves left to leftmost (0) and updates it to (X).
- The transition goes from the state (q2) to state (q1) for input X.
- The system converts the Leftmost 0 of the input tape to X.
- After updating the Leftmost 0 to X, the R/W head moves toward the right side to update the upcoming 1.

Again, according to Steps 2 and 3
R/W Head moves to the right side to update the first symbol (1) on the right side of the input tape.
The following diagram shows the input tape and Turing machine.

Again, according to Steps 4 and 01
Move Left to Leftmost 0 and update it to X.

Once again, according to steps 2 and 3
The R/W Head moves toward the right side to update the first symbol (1) on the right side of the input tape.

At this point,
- The input tape updates all 0s and 1s with X and Y, respectively.
- The current state is q2, and the R/W Head is moving toward the Left side of every input of Y.
- As X input occurs, the state goes to q0, and R/W Head moves toward the right side.
- By consuming all input Y, the state will be q3.
- As the first special symbol ($) occurs, the state goes to the final state (q4), and the R/W head will point to the last symbol of the considered language.
Hence, the following Turing machine is the acceptor of the given language.

Note: For special symbol ($), at state q0, the given language is accepted.
Example of Turing Machine for Regular Languages
Let’s explain some examples of turning machines for regular languages
Important: We can design a Turing machine for all regular expressions where the R/W head always moves towards the right. However, we can design a Turing machine for some regular languages where the R/W head moves in both directions, either left or right.
The R/W head always moves towards the right until it reaches the final state, after which it stops moving.
Turing Machine Example 01:
Construct a TM for the language L = {0n} where n≥1
Solution
The following is the Regular expression for the given example
0(0)*
The following are the all possible strings created from L = {0n}
L= {0, 00, 000, 0000,…….}
Let’s suppose a string of “0000”. R/W head movement for input tap is given below

Finally, the turning machine to accept all possible strings over language L = {0n} where n≥1 is given below

Turing Machine Example 02:
Construct a TM for the language L = {02n+1} where n≥0
Solution
The following is the Regular expression for the given example
0(00)*
The following are the all possible strings created from L = {02n+1}
L= {0, 000, 00000, 0000000,…….}
Let’s suppose a string of “000”. R/W head movement for input tap is given below

Finally, the turning machine to accept all possible strings over language L = {02n+1} where n≥0 is given below
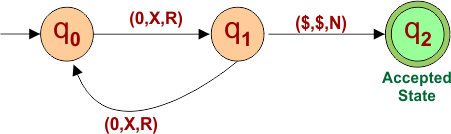
Turing Machine Example 03:
Construct a Turing machine that accepts all strings that start with 0.
Solution
The following is the Regular expression for the given example
0(0+1)*
The following are all the possible strings created
L= {0, 00, 01, 000, 011, …….}
Let’s suppose a string of “011”. R/W head movement for input tap is given below
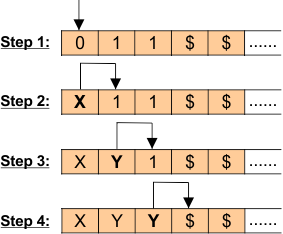
Finally, the turning machine to accept all possible strings starts with “0”

Turing Machine Example 04:
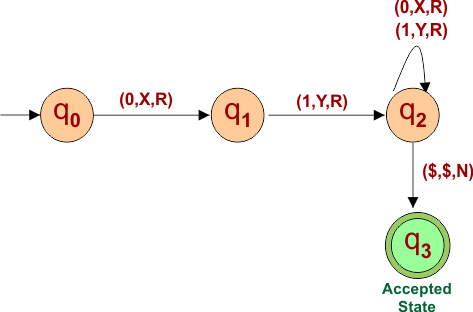
Construct a Turing machine that accepts all strings that start with 01.
Solution
The following is the Regular expression for the given example
01(0+1)*
The following are all the possible strings created
L= {01, 010, 011, 0100, 0111, …….}
Finally, the turning machine to accept all possible strings starts with “01” and is