Dead State in DFA

In automata theory, a Dead State (also known as a trap state or rejecting state) is a key concept in the design and analysis of deterministic finite automata. Whether you’re a computer science student or preparing for competitive exams like GATE or UGC NET, understanding dead states helps you optimize and analyze deterministic finite automata (DFA) effectively.

What is a Dead State?

A dead state is a state in a DFA from which no sequence of inputs can lead to an accepting (final) state. Once the automaton enters a dead state, it cannot recover or proceed to an accepting state regardless of the inputs that follow.

Key Characteristics:

  • A dead state is never an accepting or final state in the automaton.

  • Once entered, all transitions from a dead state lead either back to itself or to other dead states.

  • It typically represents a condition where the input string can no longer be accepted, indicating failure or invalid input.

Why Do We Use Dead States?

Dead states help:

  • Complete the transition function (especially in total DFAs).

  • Represent invalid or non-accepted paths explicitly.

  • Assist in error detection and rejection in language recognition.

Dead State Example

Consider a DFA that accepts only the binary string “10”.

Dead State Example in DFA

You can never reach a final state from a dead stated

Optimizing DFA Using Dead States

While dead states help in clarity, minimization algorithms may remove them if they’re not reachable or useful. However, for complete DFAs, dead states are necessary to define transitions for every possible input.

Difference Between Dead State and Unreachable State

Both the Dead State and Unreachable states are used in a DFA. Let see the comparison between these two terms through diagram and table

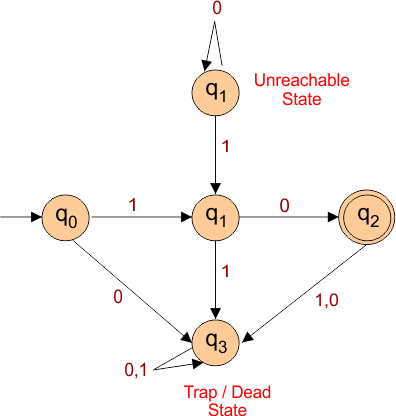
Dead State Example in DFA vs unreachable state

Feature Dead State Unreachable State
Definition A state from which no accepting state is reachable A state that cannot be reached from the start state
Usefulness Often used to handle invalid input paths Typically removed during DFA minimization
Transitions All transitions stay in itself or other dead states May have transitions, but never accessed
Detection Based on inability to reach final states Based on no incoming path from start state
Example Use Case Representing failure in pattern matching Usually eliminated to simplify automata

"Your Support, Our Priority"

"We Make It Easy"