Moore Machine Examples

In this lecture, we will explore some examples of Automata Moore Machines. During the previous lecture, we covered the topic of Moore Machines.

Example 1: Moore Machine For 1’s complement

Design a Moore machine to generate 1’s complement of a given binary number.

Solution

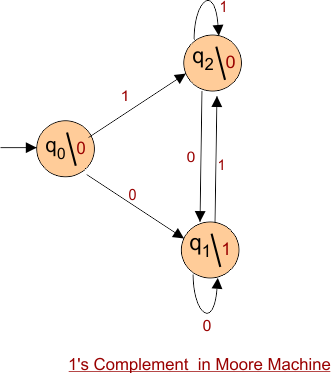
According to the first complement, if the given input is “1”, then the output will be “0”. And if the input is “0”, then the output will be “1”.

For the First complement, there should be at least three states.

• One state is the start state.
• The 2^nd state is to accept “1’s” as input and produce output as “0”.
• The 3^rd state will accept “0’s” as input and produce output as “1”.

Hence, the final Moore machine of given example 1 will be,

For instance, take one binary number 111001, then

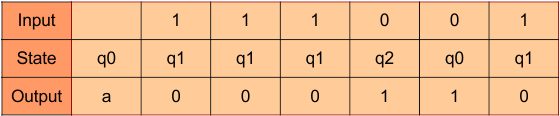
Thus, we get 0000110 as 1’s complement of 111001; we can neglect the initial 0, and the output that we get is 000110, which is 1’s complement of 111001.

Important: The output for a Moore machine is greater than the input in length by 1. Because the start state always gives an output without consuming an input.

Transition table

The Transition table of the constructed Moore Machine is given below

Thus Moore machine 6 tuples {Q, q0, ∑, O, δ, λ} are explained below where

• Q = {q0, q1, q2},
• q0 is the initial state
• ∑ = {0, 1},
• O = {0, 1}. the transition table shows the
• The remaining two tuples ( δ and λ functions) are shown in the transition table 

Example 02 –  Moore Machine

Construct an Automata Moore Machine that prints “a” whenever the sequence “01” is encountered in any input binary string.

Solution

Automata Moore Machine, for the given example, is given below