Deterministic Finite Automata
A Deterministic Finite Automata (DFA) is a key concept in theory of automata and theoretical computer science. It is a type of finite state machine that is used to recognize regular languages. Every DFA is designed to accept a regular language, which can be either finite (a finite set of strings) or infinite (an infinite set of strings).
Here are some Key Points of Deterministic Finite Automata
- Deterministic: For each state and input symbol, only one transition is allowed.
- Finite States: A DFA has a limited number of states.
- Single Initial State: There is exactly one start state.
- Accepting States: One or more final states determine accepted strings.
- Transition Function: Defined as δ: Q × Σ → Q (unique for each input).
- No ε-Moves: Null (ε) transitions are not allowed in a DFA.
- No Memory: It does not store the input string or remember past symbols.
- Consumes All Input Symbols: A DFA processes every input symbol at each state of the DFA.
- Language Recognition: DFA accepts all regular languages, which can be finite or infinite.
- String Rejects or Accepts: A string is accepted if it ends in a final state.
- Dead State: A dead state can be used in a DFA. It is a non-accepting state from which no accepting state can ever be reached.
DFA Working Flow Chart
DFA takes a language as input. If the input is accepted, then the language is considered a regular language; otherwise, it is not a regular language. The flow chart of DFA working is given below

5-Tuples of Deterministic Finite Automata
A DFA is formally represented as a 5-tuple:
DFA=(Q,Σ,δ,q0,F)
Let explain each tuple
I. Q – Finite Set of States
- Represents all possible states (always finite) the DFA can be in.
- Example:
Q = {q0, q1}
II. Σ – Input Alphabet
- A finite set of symbols that the DFA can read as input.
- Example:
Σ = {0, 1}for binary strings.
III. δ – Transition Function
- Describes how the DFA moves from one state to another based on input.
- Formally:
δ: Q × Σ → Q - Example:
δ(q0, 0) = q1means from stateq0, on input0, go toq1.
IV. q₀ – Initial State
- The starting state of the DFA.
- It must be one of the states in
Q. - Example:
q0is the initial state where the DFA begins processing input.
V. F – Set of Accepting (Final) States
- A subset of Q that contains all the accepting states.
- If the DFA ends in any state from
FAfter reading the entire input, the string is accepted. - Example:
F = {q2}
Notations in Deterministic Finite Automata
The following figure shows all basic notations of the DFA
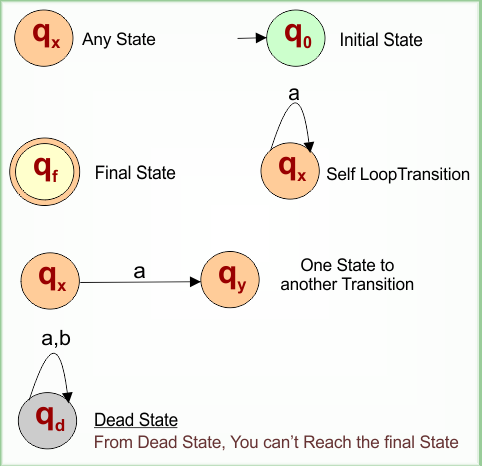
The following are the major notations of deterministic finite automata
-
Any State – A labeled circle (e.g.,
q0,q1) representing a DFA state.
➤ Visual: ○ with state name inside. -
Initial State – The starting point of DFA before any input is read.
➤ Visual: Arrow pointing into the state→ q0. -
Final State – A state where the input is accepted if DFA stops here.
➤ Visual: Double circle ○○ (e.g.,q2). -
Self-loop Transition – A transition where the state points back to itself.
➤ Visual: Arrow looping over the state:q1 —a→ q1. -
One State to Another Transition – Movement between different states on an input symbol.
➤ Visual: Arrow labeled with input symbol:q0 —a→ q1. -
Dead State – A non-final state where all transitions lead back to itself (no acceptance possible).
➤ Visual: Circle with self-loops for all inputs, usually labeledqdordead.
DFA Transition Rules
There are two basic rules used in a DFA transition
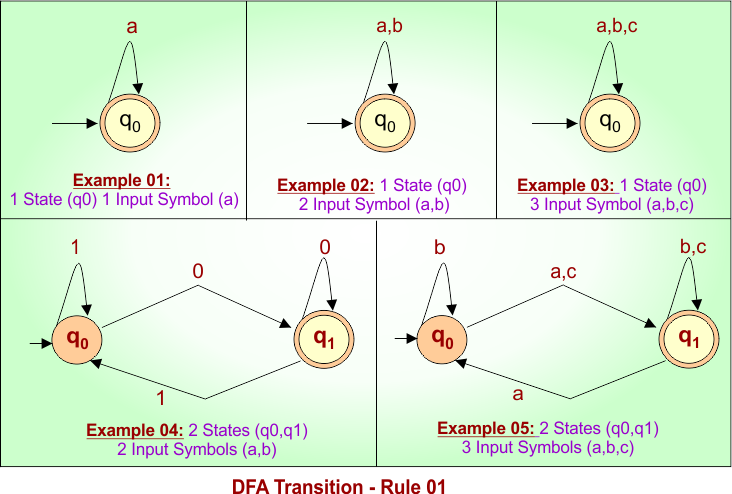
Transition Rule 01: Every state in a DFA must define a transition for each input symbol.
Follwoing figure shows 5 different examples according to Rule No. 01
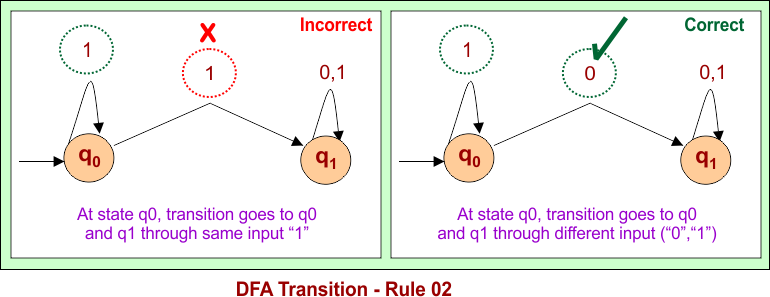
Transition Rule 02: No state in a DFA can have multiple transitions on the same input symbol.
Follwoing figure shows an example, according to Rule No. 02
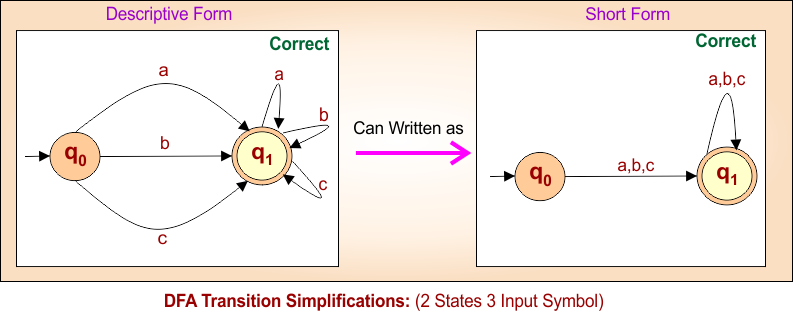
Transition Simplifications in DFA
Find Minimum States for DFA Construction
To find the minimum number of states required for DFA construction, you can follow a rule-based approach based on the type of language.
- When the length of the string (n) ≥ 1 and the initial state is a final state, then the minimum state can be 1 (not always).
- But when the initial state is not final, then the number of minimum states can be according to the following table
| Language Type | Minimum States Required | Examples |
|---|---|---|
Starts with a substring of length n |
n + 2 | Starts with “ab” |
Equals the exact string of length n |
n + 1 | Only “1011” |
Ends with a substring of length n |
n + 1 | Ends with “11” |
Contains a substring of length n |
n + 1 | Contains “ab” |
DFA Acceptance Strategy
To determine whether a DFA accepts a given string, you can follow the following acceptance strategy
- Start at the initial state.
- Read the input string one symbol at a time.
- For each symbol, follow the unique transition.
- If the string ends in a final (accepting) state, it is accepted.
- Otherwise, the string is rejected, and it is not part of that language.
Example: Here is a DFA, which accepts all the strings over the alphabet ∑ {0,1} that end with “10”.
Language with valid strings: L = {10, 010, 110, 0110, 1110, 1010, 11110,…, }
Here is the DFA for the given Language which accept the valid strings and reject the invalid strings

DFA Construction Strategy
We can easily draw an DFA by following the 5-step strategy, which is given below
- Step 01: Understand the Language and draw all possible strings
- Step 02: Find the minimum states required to design a DFA (If it is not known in certain cases, skip this step).
- Step 03: Draw transitions to accept the minimum string.
- Step 04: Add more transitions and states (if required) to complete the deterministic rules of the DFA.
- Step 05: Verify the DFA against several valid and invalid strings to ensure it only accepts the valid inputs and rejects the invalid.
Note: The Following points have already been discussed in this lecture.
|
DFA Construction Examples
Here are the Top 50 examples of Deterministic Finite Automata
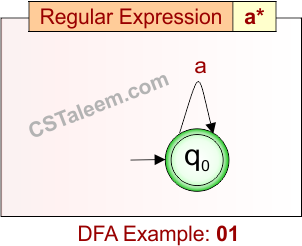
Deterministic Finite Automata: Example 01
Design a DFA for zero or more occurrences of ‘a
- Regular Expression = a*
- L = {ε, a, aa, aaa, aaaa, …}
Language contains all strings made only of ‘a’, including the empty string.
DFA for RE = a* is given below
Deterministic Finite Automata: Example 02
Design a DFA for zero or more occurrences of ‘a’ or ‘b’
- Regular Expression = (a+b)*
- L = {ε, a, b, aa, ab, ba, bb, aaa, abb, …}
Language contains all strings made using any combination of ‘a’ and ‘b’, including the empty string.
DFA for RE = (a+b)* is given below

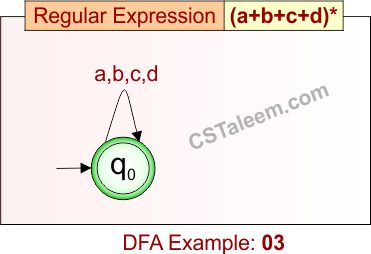
Deterministic Finite Automata: Example 03
Design a DFA for zero or more occurrences of ‘a’, ‘b’, ‘c’, or ‘d’
- Regular Expression = (a+b+c+d)*
- L = {ε, a, b, c, d, ab, ac, ad, ba, bb, …, abcd, dbca, …}
Language contains all strings made using any combination of ‘a’, ‘b’, ‘c’, and ‘d’, including the empty string.
DFA for RE = (a+b+c+d)* is given below
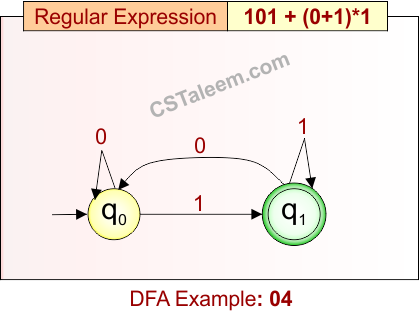
Deterministic Finite Automata: Example 04
Design a DFA for strings that are either exactly ‘101’ or end with ‘1’
- Regular Expression = 101 + (0+1)*1
- L = {101, 1, 01, 001, 101, 0001, 1111, …}
Language contains all strings that are exactly ‘101’ or any string over {0,1} that ends with ‘1’.
DFA for RE = 101 + (0+1)*1 is given below
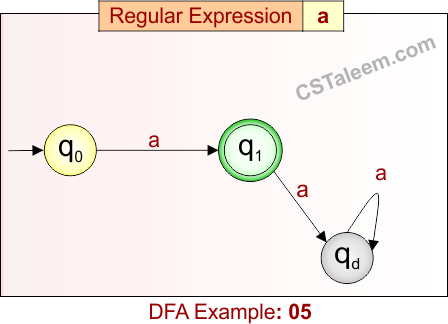
Deterministic Finite Automata: Example 05
Design a DFA for the string that is exactly ‘a’
- Regular Expression = a
- L = {a}
Language contains only one string: exactly a single ‘a’.
DFA for RE = a is given below
Deterministic Finite Automata: Example 06
Design a DFA for the string that is either ‘a’ or ‘b’
- Regular Expression = a + b
- L = {a, b}
Language contains only two strings: ‘a’ or ‘b’.
DFA for RE = a + b is given below
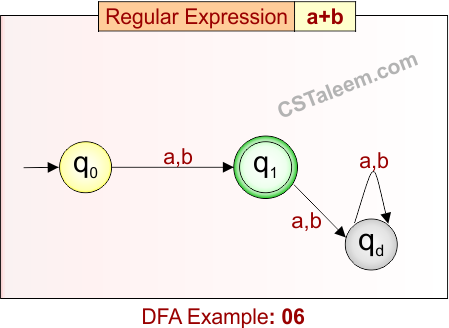
Deterministic Finite Automata: Example 07
Design a DFA for strings that start with ‘a’ followed by any combination of ‘a’ or ‘b’
- Regular Expression = a(a + b)*
- L = {a, aa, ab, aba, abb, aab, aaaa, …}
Language contains all strings that begin with ‘a’ and are followed by zero or more symbols from {a, b}.
DFA for RE = a(a + b)* is given below
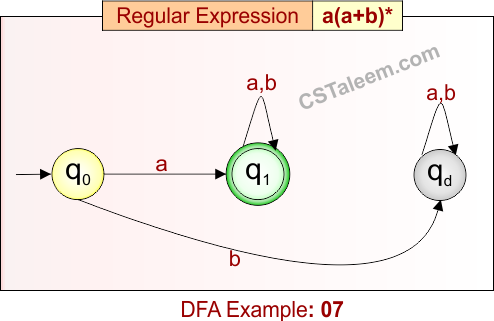
Deterministic Finite Automata: Example 08
Design a DFA for zero or more occurrences of ’10’ or ‘1’
- Regular Expression = (10 + 1)*
- L = {ε, 1, 10, 11, 101, 1010, 1110, 10110, …}
Language contains all strings formed by repeating ‘1’ or ’10’ any number of times, including the empty string.
DFA for RE = (10 + 1)* is given below
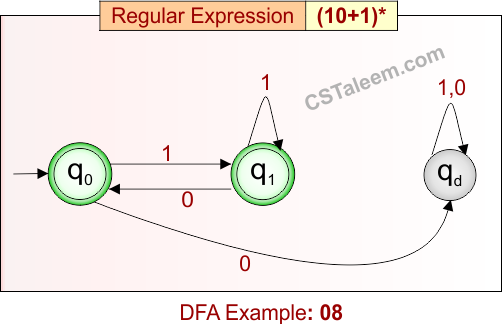
Deterministic Finite Automata: Example 09
Design a DFA for strings that start with ‘a’ followed by zero or more ‘bb’ pairs, then any combination of ‘a’ or ‘b’
- Regular Expression = (a(bb)*)(a + b)*
- L = {a, abb, abbaa, abbb, abba, abbab, abbbba, abbbbb, …}
Language contains all strings that begin with ‘a’, followed by zero or more repetitions of “bb”, and then any number of ‘a’s or ‘b’s.
DFA for RE = (a(bb)*)(a + b)* is given below
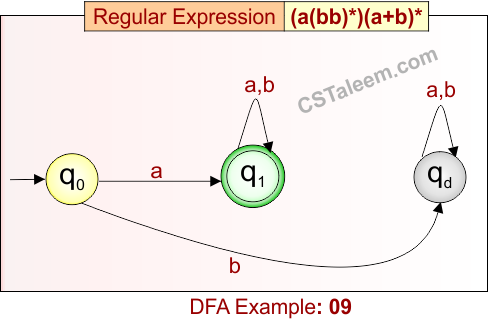
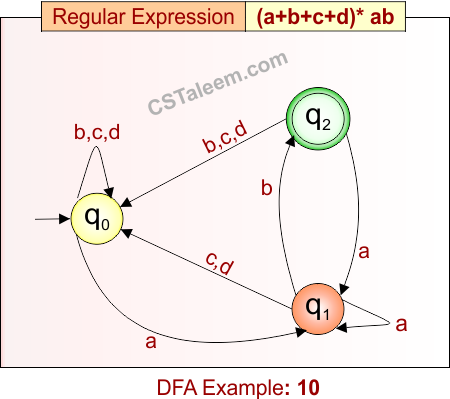
Deterministic Finite Automata: Example 10
Design a DFA for strings that end with ‘ab’ and may have any combination of ‘a’, ‘b’, ‘c’, or ‘d’ before it
- Regular Expression = (a + b + c + d)*ab
- L = {ab, aab, cab, dab, cdab, ddab, bacdab, …}
Language contains all strings over {a, b, c, d} that end with the substring “ab”.
DFA for RE = (a + b + c + d)*ab is given below
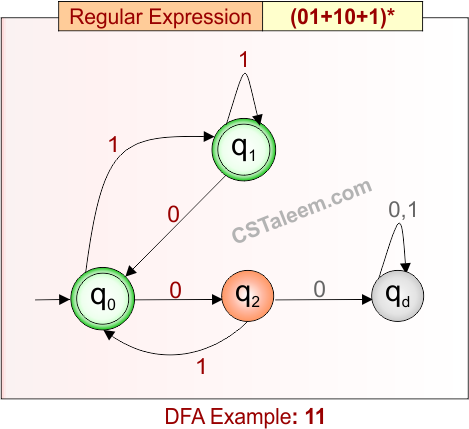
Deterministic Finite Automata: Example 11
Design a DFA for zero or more occurrences of ’01’, ’10’, or ‘1’
- Regular Expression = (01 + 10 + 1)*
- L = {ε, 1, 01, 10, 101, 0110, 1101, 1010, 111, …}
Language contains all strings formed by repeating any combination of ’01’, ’10’, or ‘1’, including the empty string.
DFA for RE = (01 + 10 + 1)* is given below
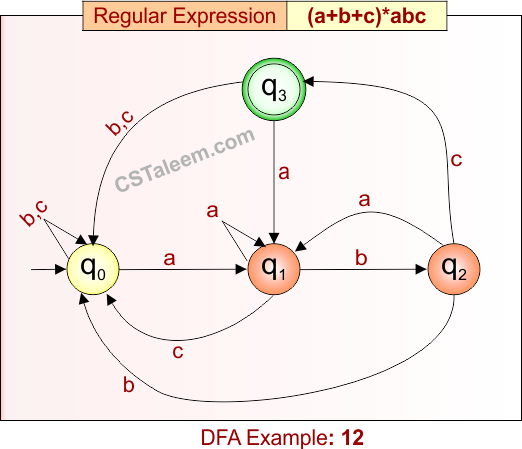
Deterministic Finite Automata: Example 12
Design a DFA for strings that end with ‘abc’ and may have any combination of ‘a’, ‘b’, or ‘c’ before it
- Regular Expression = (a + b + c)*abc
- L = {abc, aabc, babc, cabc, ababc, ccbabc, …}
- Some rejected strings = {ab, ac, abca, aacb, bc, cba, …}
Language contains all strings over {a, b, c} that end with the substring “abc”.
DFA for RE = (a + b + c)*abc is given below
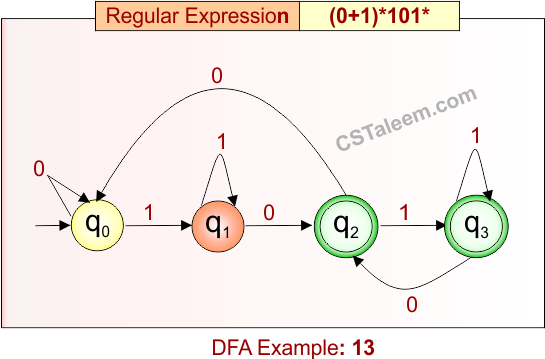
Deterministic Finite Automata: Example 13
Design a DFA for strings that contain ’10’ followed by zero or more ‘1’s, with any combination of ‘0’ or ‘1’ before it
- Regular Expression = (0 + 1)*101*
- L = {10, 101, 1011, 0010, 1101, 00010111, …}
- Some rejected strings = {1, 0, 11, 100, 1110, 0011, …}
Language contains all strings over {0, 1} that include the substring “10” followed by zero or more 1’s.
DFA for RE = (0 + 1)*101* is given below
Deterministic Finite Automata: Example 14
Design a DFA for strings that start with ’10’, followed by zero or more ‘1’s, and then any combination of ‘0’ or ‘1’
- Regular Expression = 101*(0 + 1)*
- L = {10, 101, 1010, 1011, 10110, 1011110, …}
- Some rejected strings = {1, 0, 11, 0010, 110, …}
Language contains all strings that begin with “10”, optionally followed by more ‘1’s, and then any mix of ‘0’s and ‘1’s.
DFA for RE = 101*(0 + 1)* is given below**
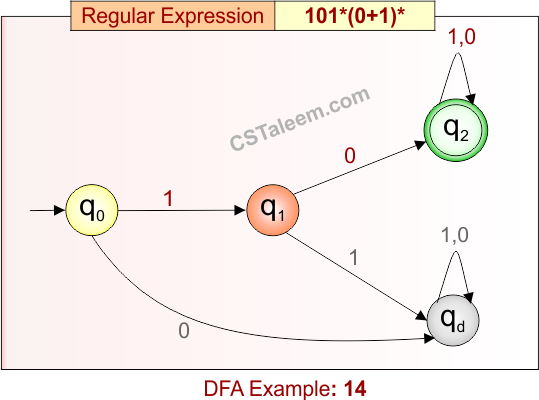
Deterministic Finite Automata: Example 15
Design a DFA for strings that start with ‘bab’ followed by any combination of ‘a’ or ‘b’
- Regular Expression = bab(a + b)*
- L = {bab, baba, babb, babaa, babab, babba, babbbb, …}
- Some rejected strings = {ba, ab, bbab, ababa, bba, …}
Language contains all strings that begin with “bab”, followed by zero or more symbols from {a, b}.
DFA for RE = bab(a + b)* is given below
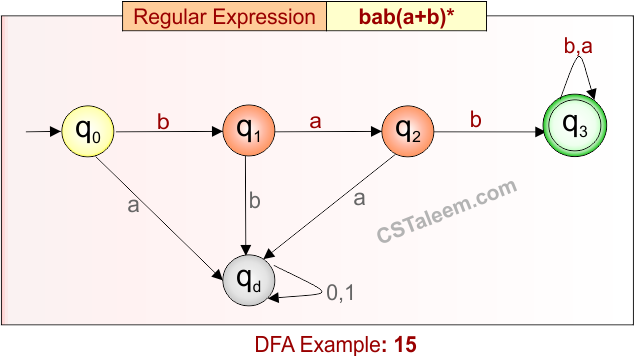
Deterministic Finite Automata: Example 16
Design a DFA for strings that start and end with the same bit (either ‘1’…‘1’ or ‘0’…‘0’), with any combination of ‘0’ or ‘1’ in between
- Regular Expression = 1(1 + 0)*1 + 0(1 + 0)*0
- L = {11, 101, 1001, 1101, 010, 0010, 0000, 0110, …}
- Some rejected strings = {1, 0, 10, 01, 1010, 011, 110, …}
Language contains all strings over {0,1} that start and end with the same bit, and are at least two characters long.
DFA for RE = 1(1 + 0)*1 + 0(1 + 0)*0 is given below
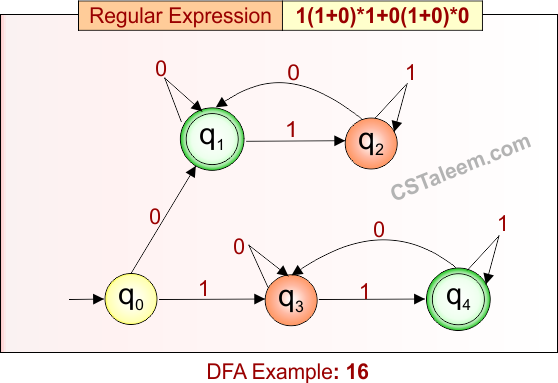
Deterministic Finite Automata: Example 17
Design a DFA for strings that start with ’10’, end with ‘1’, and have any combination of ‘101’, ‘0’, or ‘1’ in between
- Regular Expression = 10(101 + 0 + 1)*1
- L = {101, 1001, 10101, 101011, 100101, 101101, …}
- Some rejected strings = {10, 1010, 11, 100, 101100, 0, 1, …}
Language contains all strings that begin with “10”, end with “1”, and contain any number of repetitions of “101”, “0”, or “1” in between.
DFA for RE = 10(101 + 0 + 1)*1 is given below
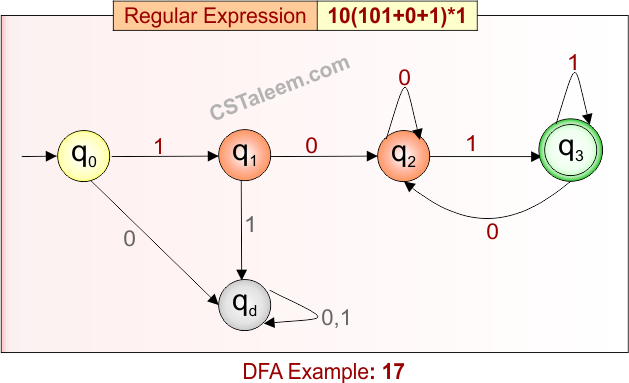
Deterministic Finite Automata: Example 18
Design a DFA for strings that are either a single ‘a’ or start with ‘a’, followed by any combination of ‘a’ or ‘b’, and ending with ‘ba’
- Regular Expression = a(a + b)*ba + a
- L = {a, aba, abba, aaba, aaabba, abbba, …}
- Some rejected strings = {b, ab, ba, aa, abab, abb, baa, …}
Language contains strings that are either exactly “a” or start with ‘a’, followed by any number of ‘a’s and ‘b’s, and end with “ba”.
DFA for RE = a(a + b)*ba + a is given below
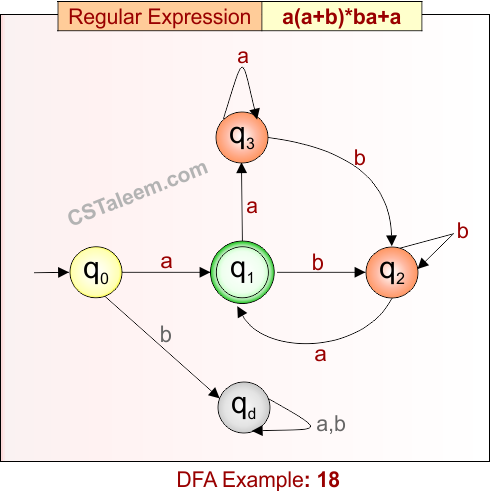
Deterministic Finite Automata: Example 19
Design a DFA for zero or more repetitions of ‘ab’, ‘bb’, ‘cc’, or ‘dd’
- Regular Expression = (ab + bb + cc + dd)*
- L = {ε, ab, bb, cc, dd, abbb, abccdd, bbabcc, ddab, …}
- Some rejected strings = {a, b, c, d, abc, bbc, bbd, abbd, cd, …}
Language contains all strings formed by repeating any number (including zero) of the substrings “ab”, “bb”, “cc”, or “dd”.
DFA for RE = (ab + bb + cc + dd)* is given below
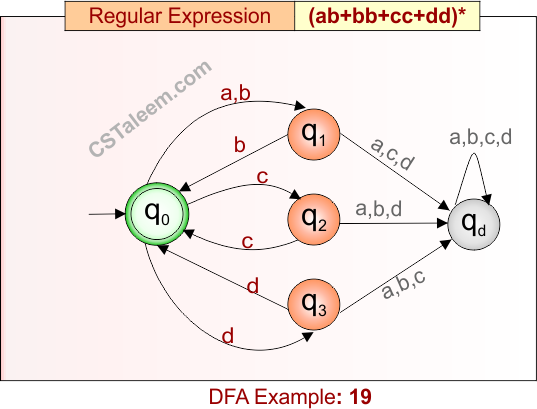
Deterministic Finite Automata: Example 20
Design a DFA for strings that are either ‘aa’, ‘ba’, or any number of repetitions of ‘aa’ and ‘b’
- Regular Expression = aa + ba + (aa + b)*
- L = {ε, aa, ba, b, bb, aaaabb, aab, bbaa, bbaab, …}
- Some rejected strings = {a, ab, bab, aba, aabbba, …}
Language contains strings that are either exactly ‘aa’, ‘ba’, or any number of repetitions of ‘aa’ and ‘b’ (including the empty string if not starting with aa or ba).
DFA for RE = aa + ba + (aa + b)* is given below
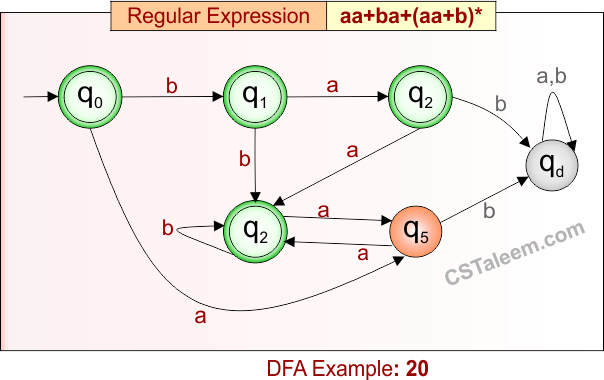
Deterministic Finite Automata: Example 21
Design a DFA for strings that are either exactly ‘ba’ or any number of repetitions of ‘aa’ and ‘b’
- Regular Expression = ba + (aa + b)*
- L = {ε, ba, b, bb, aa, aab, bba, aabaa, bbbaa, …}
- Some rejected strings = {a, ab, aba, baa, bab, abaa, aaa, …}
Language contains strings that are either exactly ‘ba’, or built from any number of ‘aa’ and ‘b’ in any order.
DFA for RE = ba + (aa + b)* is given below
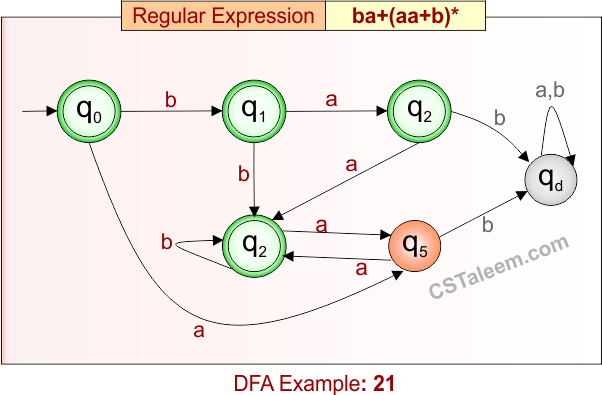
Deterministic Finite Automata: Example 22
Design a DFA for strings with zero or more repetitions of ’11’, followed by ‘0’ or ‘1’, and ending with ’00’
- Regular Expression = (11)*(0 + 1)(00)
- L = {100, 1100, 111100, 11111100, 1111100, 01100, …}
- Some rejected strings = {ε, 00, 11, 01, 1111, 110, 111, 1011, …}
Language contains strings that may start with repeated “11”, then have either a ‘0’ or ‘1’, and must end with “00”.
DFA for RE = (11)*(0 + 1)(00) is given below
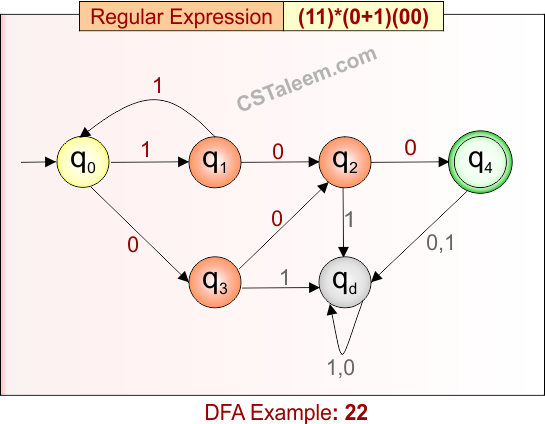
Deterministic Finite Automata: Example 23
Design a DFA for strings with zero or more ‘1’s, followed by either ‘0’ or ‘1’, and then zero or more repetitions of ’00’
Regular Expression = (1)*(0 + 1)(00)*
L = {0, 1, 10, 100, 1100, 11100, 1110000, …}
Some rejected strings = {ε, 00, …}
Language contains strings that start with any number of ‘1’s, followed by a single ‘0’ or ‘1’, and may end with zero or more “00”s.
DFA for RE = (1)*(0 + 1)(00)* is given below
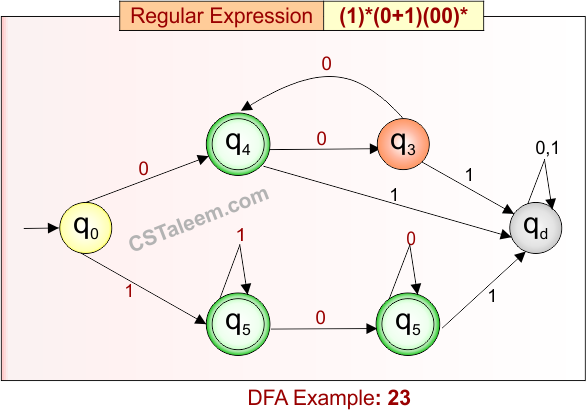
Deterministic Finite Automata: Example 24
Design a DFA for strings that are either:
-
Zero or more repetitions of “00” followed by ‘0’ or ‘1’, or
-
Zero or more repetitions of ‘1’ alone
Regular Expression = (00)*(0 + 1) + (1)*
L = {0, 1, 11, 111, 001, 0001, 0000, 000001, …}
Some rejected strings = {00, 10, 100, 101, 011, …}
Language contains either strings made of only ‘1’s (including empty), or strings starting with even number of 0’s followed by a single 0 or 1.
DFA for RE = (00)*(0 + 1) + (1)* is given below
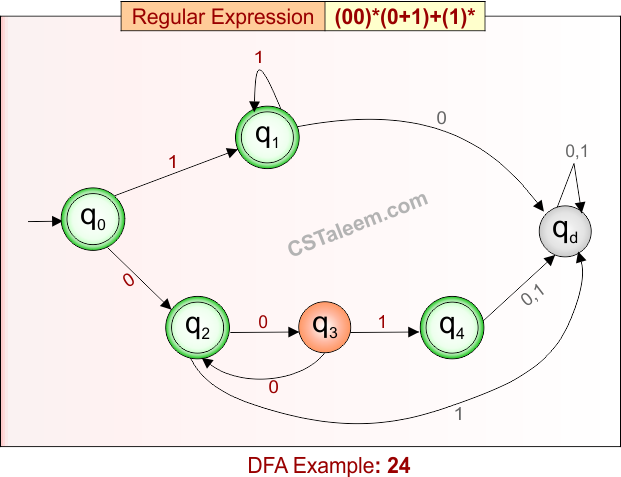
Deterministic Finite Automata: Example 25
Design a DFA for strings that are either:
-
Exactly ‘0’,
-
Or ‘1’ followed by zero or more ‘0’s and then a ‘0’ or ‘1’,
-
Or any number of ‘1’s (including the empty string)
Regular Expression = 0 + 10*(0 + 1) + (1)*
- L = {ε, 0, 1, 11, 111, 10, 100, 1000, 1001, 101, …}
- Some rejected strings = {00, 110, 001, 010, 1110, 1010, …}
Language contains:
-
A single 0
-
OR strings that begin with ‘1’, followed by zero or more ‘0’s and then a ‘0’ or ‘1’
-
OR strings made up entirely of ‘1’s
DFA for RE = 0 + 10*(0 + 1) + (1)* is given below
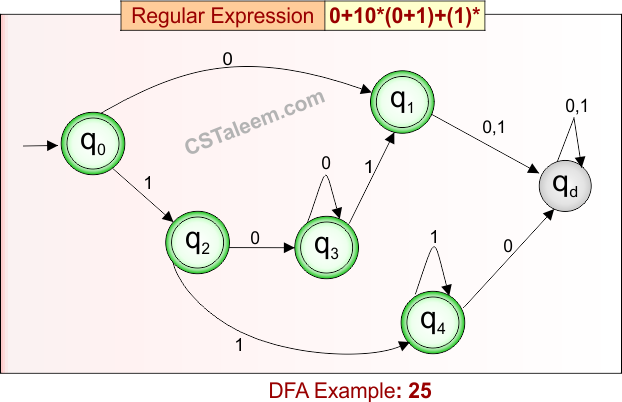
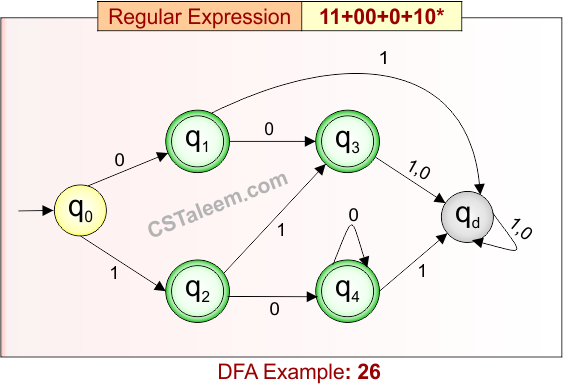
Deterministic Finite Automata: Example 26
Design a DFA for strings that are either:
- Exactly “11”,
- Exactly “00”,
- Exactly “0”,
- Or “1” followed by zero or more “0”s
Regular Expression = 11 + 00 + 0 + 10*
- L = {11, 00, 0, 10, 100, 1000, 10000, …}
- Some rejected strings = {ε, 1, 01, 101, 110, 000, 111, …}
Language contains only specific patterns: “11”, “00”, “0”, or strings starting with “1” and followed by any number of “0”s (including none).
DFA for RE = 11 + 00 + 0 + 10* is given below
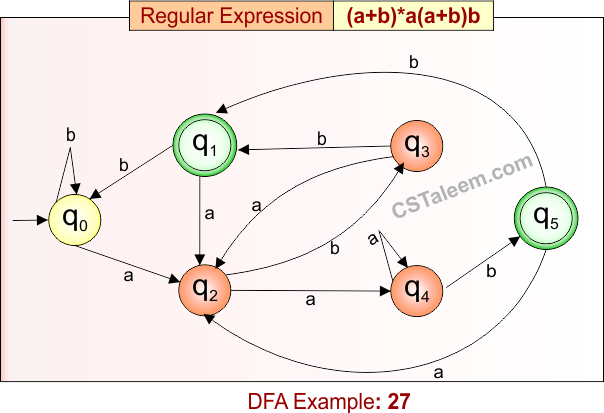
Deterministic Finite Automata: Example 27
Design a DFA for strings that contain any combination of ‘a’ and ‘b’, followed by an ‘a’, then any one symbol from {a, b}, and ending with a ‘b’
- Regular Expression = (a + b)*a(a + b)b
- L = {aab, ababb, aaab, babaab, …}
- Some rejected strings = {ε, a, b, ab, ba, aa, bb, …}
DFA for RE = (a + b)*a(a + b)b is given below
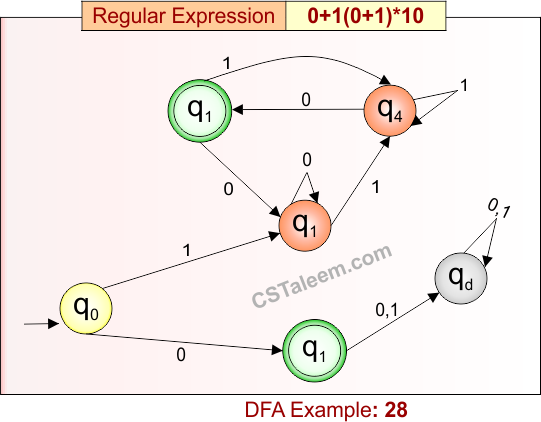
Deterministic Finite Automata: Example 28
Design a DFA for strings that are either exactly ‘0’ or start with ‘1’, followed by any combination of ‘0’ and ‘1’, and end with ’10’
- Regular Expression = 0 + 1(0 + 1)*10
- L = {0, 110, 1010, 10010, 1110, 100110, …}
- Some rejected strings = {1, 10, 00, 011, 100, 1101, 111, …}
DFA for RE = 0 + 1(0 + 1)*10 is given below
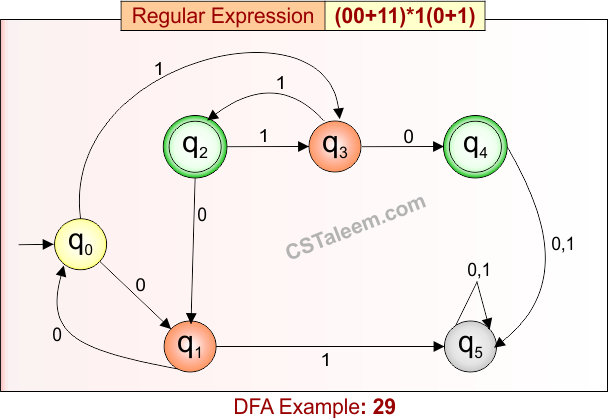
Deterministic Finite Automata: Example 29
Design a DFA for strings that consist of zero or more repetitions of ’00’ or ’11’, followed by a ‘1’, and ending with either ‘0’ or ‘1’
- Regular Expression = (00 + 11)*1(0 + 1)
- L = {10, 11, 0010, 0011, 00110010, 001111, …}
- Some rejected strings = {ε, 0, 00, 01, 110, 001100, 1000, …}
DFA for RE = (00 + 11)*1(0 + 1) is given below
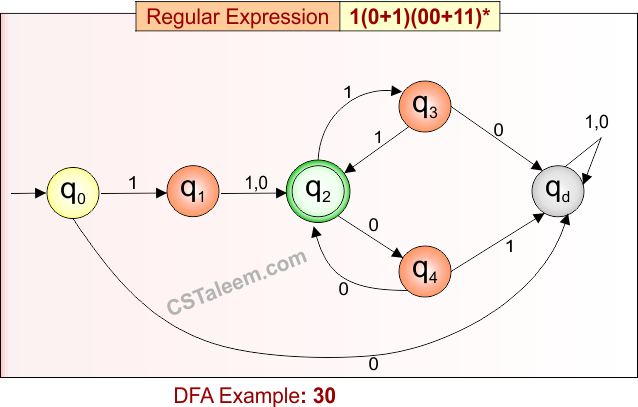
Deterministic Finite Automata: Example 30
Design a DFA for strings that start with ‘1’, followed by either ‘0’ or ‘1’, and then zero or more repetitions of ’00’ or ’11’
Regular Expression = 1(0 + 1)(00 + 11)*
L = {10, 11, 1000, 1111, 100011, 110000, 10110011, …}
Some rejected strings = {ε, 0, 1, 00, 01, 1010, 1110, 1101, …}
Language contains strings that start with ‘1’, then have one symbol from {0,1}, and then zero or more pairs of either ’00’ or ’11’.
DFA for RE = 1(0 + 1)(00 + 11)* is given below
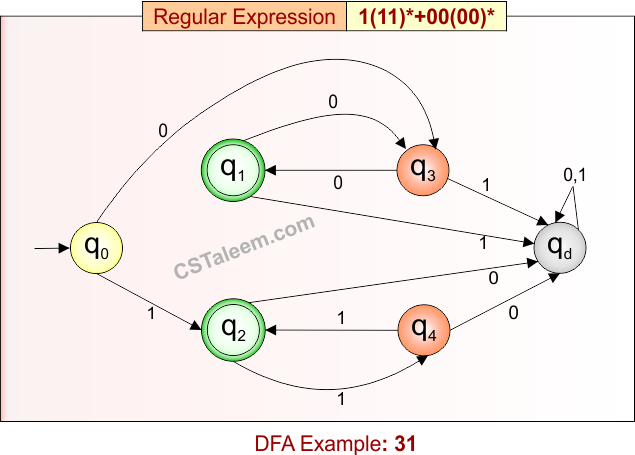
Deterministic Finite Automata: Example 31
Design a DFA for strings that are either:
-
A single ‘1’ followed by zero or more repetitions of “11”,
-
or “00” followed by zero or more repetitions of “00”
Regular Expression = 1(11)* + 00(00)*
- L = {1, 111, 11111, 00, 0000, 000000, 1111111, 00000000, …}
- Some rejected strings = {11, 0, 10, 001, 100, 1110, 0001, …}
Language contains either strings starting with ‘1’ and followed by even number of ‘1’s, or strings starting with “00” and followed by even number of ‘0’s.
DFA for RE = 1(11)* + 00(00)* is given below
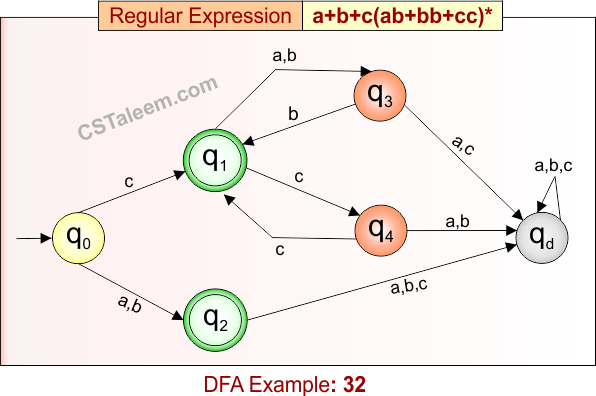
Deterministic Finite Automata: Example 32
Design a DFA for strings that are either:
-
Exactly ‘a’, ‘b’,
-
Or ‘c’ followed by zero or more repetitions of “ab”, “bb”, or “cc”
Regular Expression = a + b + c(ab + bb + cc)*
- L = {a, b, c, cab, cbb, ccc, cabbb, cabab, cbbcc, cabbbccab, …}
- Some rejected strings = {ab, ca, cb, cac, cba, cbc, abc, bac, …}
Language contains strings that are exactly ‘a’ or ‘b’, or start with ‘c’ and are followed by any number (including zero) of “ab”, “bb”, or “cc” blocks.
DFA for RE = a + b + c(ab + bb + cc)* is given below
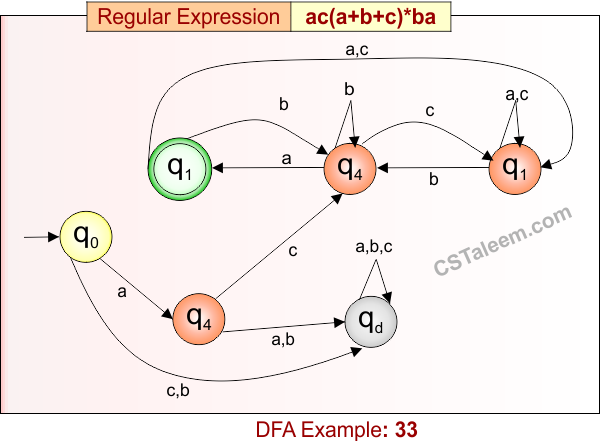
Deterministic Finite Automata: Example 33
Design a DFA for strings that start with ‘ac’, followed by any combination of ‘a’, ‘b’, or ‘c’, and end with ‘ba’
- Regular Expression = ac(a + b + c)*ba
- L = {acba, acaba, acbba, accba, acabcba, acacacba, …}
- Some rejected strings = {ac, acb, acbb, acbca, ba, abca, aca, …}
Language contains all strings that begin with “ac”, end with “ba”, and have any sequence of ‘a’, ‘b’, or ‘c’ in between.
DFA for RE = ac(a + b + c)*ba is given below
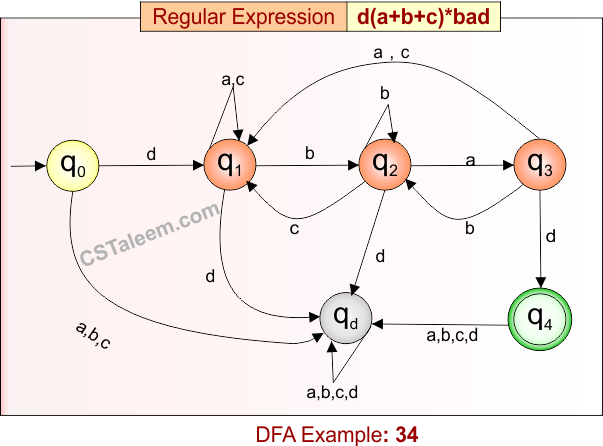
Deterministic Finite Automata: Example 34
Design a DFA for strings that start with ‘d’, followed by any combination of ‘a’, ‘b’, or ‘c’, and end with ‘bad’
- Regular Expression = d(a + b + c)*bad
- L = {dbad, dabcbad, dabcabcabcbad, daaaabcbad, …}
- Some rejected strings = {d, bad, dbac, dabcad, dab, daaad, …}
Language contains all strings that begin with “d”, end with “bad”, and have any sequence of ‘a’, ‘b’, or ‘c’ in between.
DFA for RE = d(a + b + c)*bad is given below
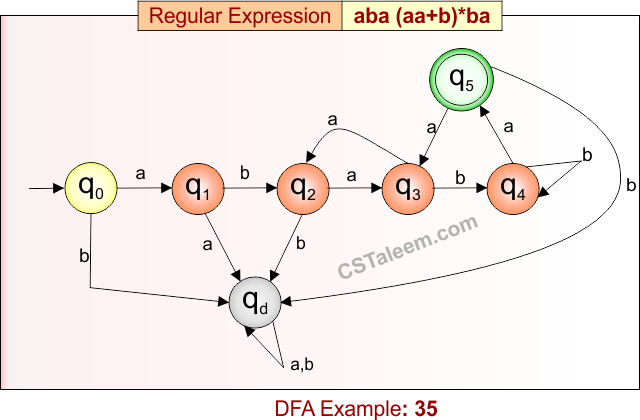
Deterministic Finite Automata: Example 35
Design a DFA for strings that start with ‘aba’, followed by any number of repetitions of ‘aa’ or ‘b’, and end with ‘ba’
- Regular Expression = aba(aa + b)*ba
- L = {ababa, ababba, ababba, ababbaaaaba, …}
- Some rejected strings = {aba, abaa, abba, abaaa, abab, ababaaa, …}
Language contains all strings that begin with “aba”, end with “ba”, and in between may have zero or more repetitions of “aa” or “b”.
DFA for RE = aba(aa + b)*ba is given below
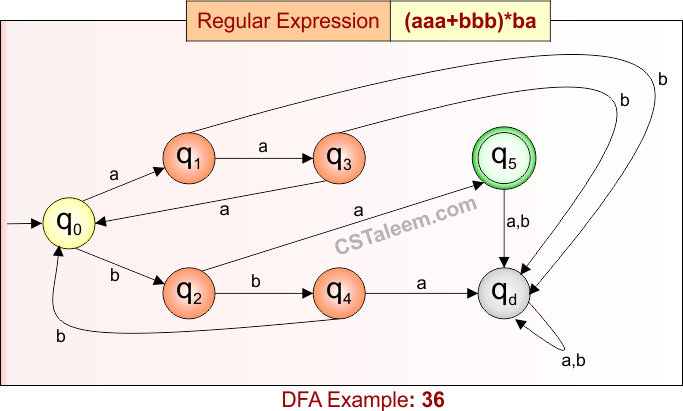
Deterministic Finite Automata: Example 36
Design a DFA for strings formed by zero or more repetitions of ‘aaa’ or ‘bbb’, followed by ‘ba’
- Regular Expression = (aaa + bbb)*ba
- L = {ba, aaabbbba, bbbba, aaaba, aaabbbaaaba, …}
- Some rejected strings = {a, b, aaa, bbb, abab, baa, abba, aaab, …}
Language contains strings that end in “ba”, and may have zero or more blocks of “aaa” or “bbb” before it.
DFA for RE = (aaa + bbb)*ba is given below
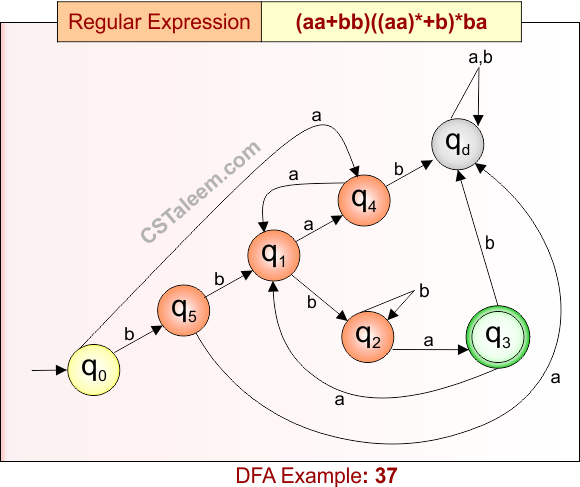
Deterministic Finite Automata: Example 37
Design a DFA for strings that start with ‘aa’ or ‘bb’, followed by any combination of zero or more ‘aa’ blocks or single ‘b’s, and end with ‘ba’
- Regular Expression = (aa + bb)((aa)* + b)*ba
- L = {aaba, bbbaa, aaaaba, bbaabba, bbaabba, aabbaabba, …}
- Some rejected strings = {ba, aba, aab, bbb, aaab, abba, ababa, …}
Language contains strings that start with “aa” or “bb”, may include any number of ‘aa’ or ‘b’, and must end in “ba”.
DFA for RE = (aa + bb)((aa)* + b)*ba is given below
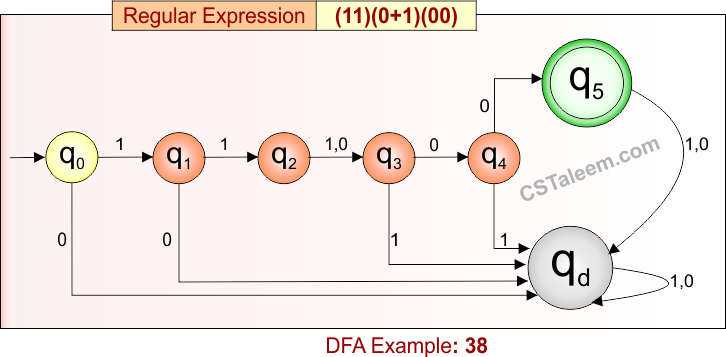
Deterministic Finite Automata: Example 38
Design a DFA for strings that start with ’11’, followed by either ‘0’ or ‘1’, and end with ’00’
- Regular Expression = (11)(0 + 1)(00)
- L = {11000, 11100}
- Some rejected strings = {11, 110, 111, 1000, 0000, 11001, …}
Language contains only strings that begin with “11”, then have a single ‘0’ or ‘1’, and end with “00”.
DFA for RE = (11)(0 + 1)(00) is given below
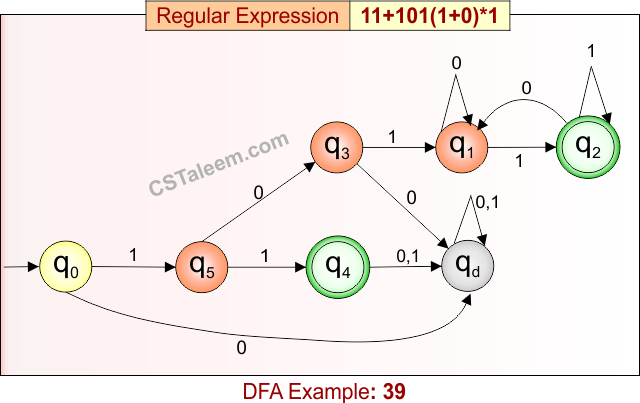
Deterministic Finite Automata: Example 39
Design a DFA for strings that are either exactly ’11’ or start with ‘101’, followed by any combination of ‘0’ or ‘1’, and ending with ‘1’
- Regular Expression = 11 + 101(1 + 0)*1
- L = {11, 1011, 10101, 101001, 101111, 1010000001, …}
- Some rejected strings = {1, 0, 101, 1001, 1010, 111, 101100, …}
Language contains either:
- The exact string “11”, OR
- Strings that begin with “101”, followed by any mix of 0s and 1s, and ending in “1”.
DFA for RE = 11 + 101(1 + 0)*1 is given below
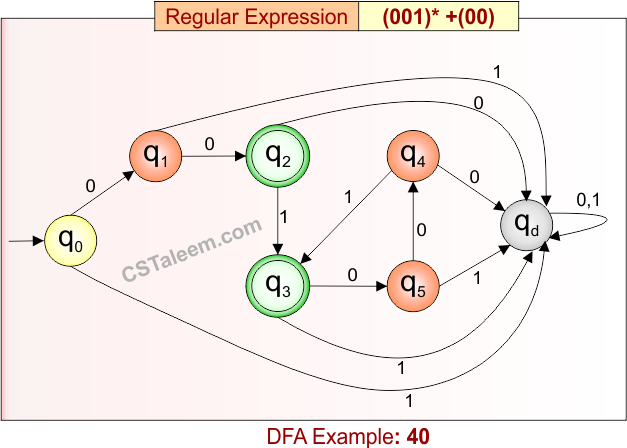
Deterministic Finite Automata: Example 40
Design a DFA for strings that are either zero or more repetitions of “001”, or exactly “00”
- Regular Expression = (001)* + (00)
- L = {ε, 001, 001001, 001001001,…………., 00}
- Some rejected strings = {0, 1, 01, 000, 0010, 00100, 010, …}
Language contains either:
-
the exact string “00”, or
-
any number (including zero) of the substring “001” repeated.
DFA for RE = (001)* + (00) is given below
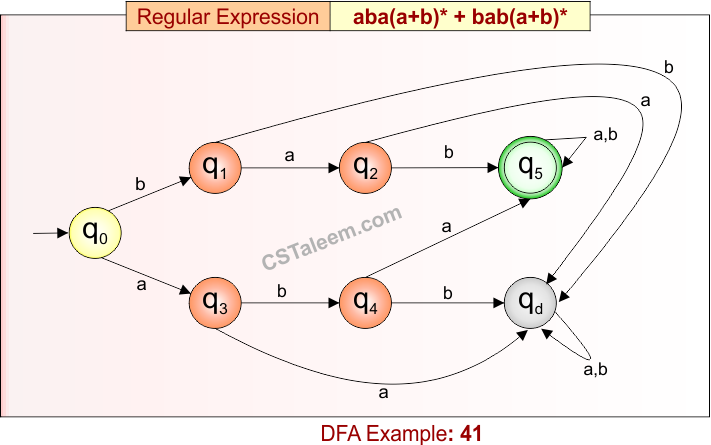
Deterministic Finite Automata: Example 41
Design a DFA for strings that start with ‘aba’ or ‘bab’, followed by any combination of ‘a’ or ‘b’
- Regular Expression = aba(a + b)* + bab(a + b)*
- L = {aba, abab, abaa, ababb, bab, baba, babb, …}
- Some rejected strings = {a, b, ab, ba, abb, baa, …}
Language contains all strings that begin with either ‘aba’ or ‘bab’, followed by any number of ‘a’ or ‘b’.
DFA for RE = aba(a + b)* + bab(a + b)* is given below
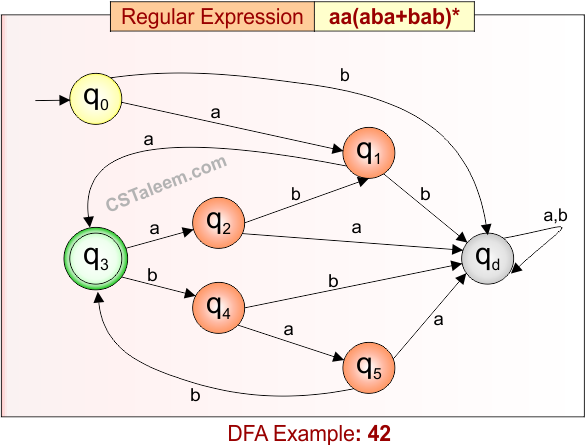
Deterministic Finite Automata: Example 42
Design a DFA for strings that start with ‘aa’, followed by zero or more repetitions of ‘aba’ or ‘bab’
- Regular Expression = aa(aba + bab)*
- L = {aa, aaaba, aaababab, aaabababbab, …}
- Some rejected strings = {a, aaa, aab, aaba, aabba, abaa, aabaa, …}
Language contains all strings that begin with “aa”, and are followed by zero or more repetitions of “aba” or “bab”.
DFA for RE = aa(aba + bab)* is given below
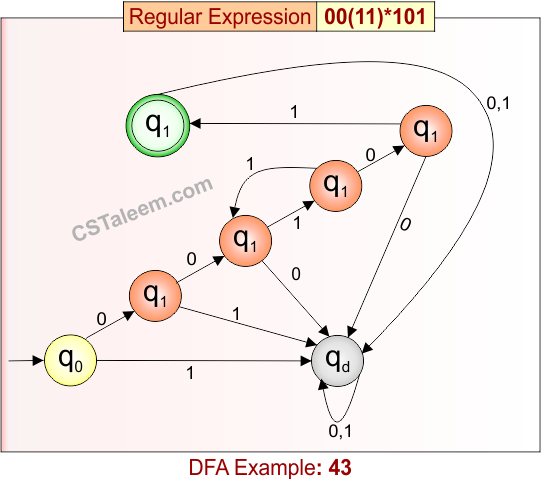
Deterministic Finite Automata: Example 43
Design a DFA for strings that start with ’00’, followed by zero or more repetitions of ’11’, and ending with ‘101’
- Regular Expression = 00(11)*101
- L = {00101, 0011101, 001111101, …}
- Some rejected strings = {00, 001, 0010, 00100, 01101, 000101, …}
Language contains strings that begin with “00”, may have zero or more “11” pairs, and must end with “101”.
DFA for RE = 00(11)*101 is given below
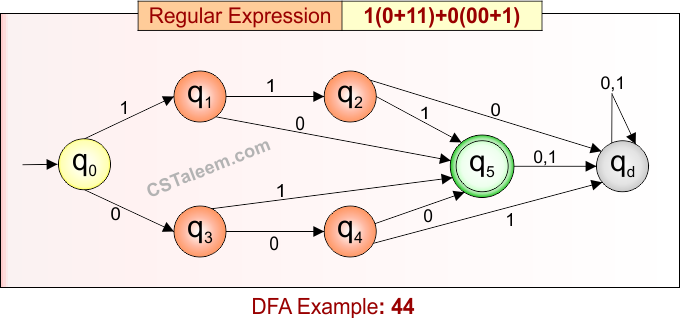
Deterministic Finite Automata: Example 44
Design a DFA for strings that are either:
-
‘1’ followed by ‘0’ or ’11’,
-
OR ‘0’ followed by ’00’ or ‘1’
Regular Expression = 1(0 + 11) + 0(00 + 1)
- L = {10, 111, 000, 01}
- Some rejected strings = {1, 0, 11, 001, 100, 1011, 0001, …}
Language contains exactly four valid strings: “10”, “111”, “000”, and “01”.
DFA for RE = 1(0 + 11) + 0(00 + 1) is given below
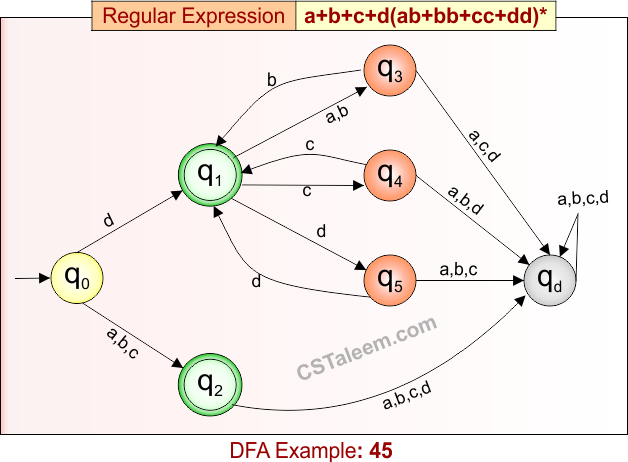
Deterministic Finite Automata: Example 45
Design a DFA for strings that are either exactly ‘a’, ‘b’, or ‘c’, or start with ‘d’ followed by zero or more repetitions of ‘ab’, ‘bb’, ‘cc’, or ‘dd’
- Regular Expression = a + b + c + d(ab + bb + cc + dd)*
- L = {a, b, c, d, dab, dbb, dcc, ddd, , dbbabdd, …}
- Some rejected strings = {ab, da, dc, dbc, dbbd, ddabbdc, dabba, …}
Language contains:
-
Single-symbol strings: “a”, “b”, “c”, or
-
Strings starting with “d”, followed by any number of “ab”, “bb”, “cc”, or “dd”
DFA for RE = a + b + c + d(ab + bb + cc + dd)* is given below
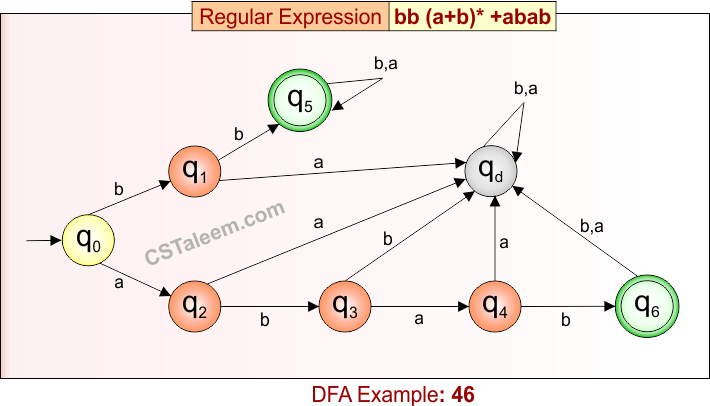
Deterministic Finite Automata: Example 46
Design a DFA for strings that either start with ‘bb’ followed by any combination of ‘a’ or ‘b’, or are exactly ‘abab’
Regular Expression = bb(a + b)* + abab
L = {bb, bba, bbb, bbaa, bbab, bbaba,……., abab}
Some rejected strings = {ab, ba, aabb, abba, baba, aba, …}
Language contains:
-
All strings that begin with “bb” and continue with any number of ‘a’ or ‘b’,
-
Or the exact string “abab”
DFA for RE = bb(a + b)* + abab is given below
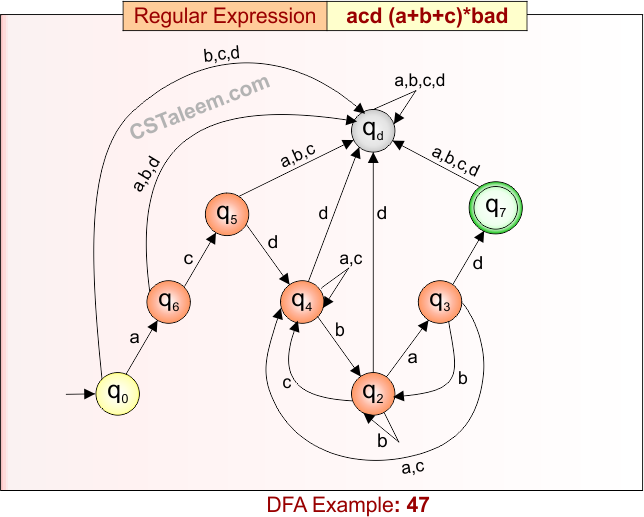
Deterministic Finite Automata: Example 47
Design a DFA for strings that start with ‘acd’, followed by any combination of ‘a’, ‘b’, or ‘c’, and end with ‘bad’
- Regular Expression = acd(a + b + c)*bad
- L = {acdbad, acdabad, acdbcbad, acdabcbabcbad, …}
- Some rejected strings = {acd, bad, acdb, acdba, acdbc, acdcba, …}
Language contains all strings that begin with “acd”, end with “bad”, and have any sequence of ‘a’, ‘b’, or ‘c’ in between.
DFA for RE = acd(a + b + c)*bad is given below
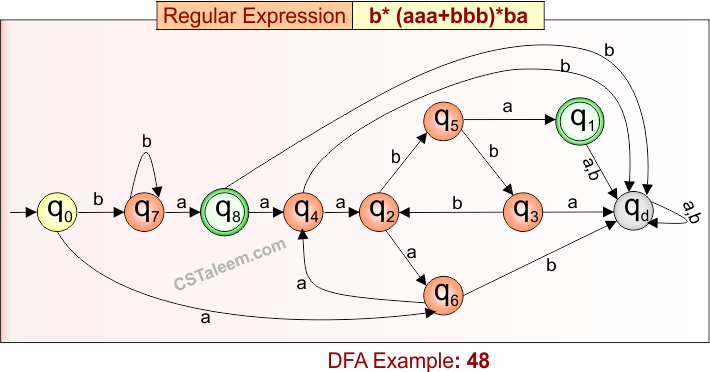
Deterministic Finite Automata: Example 48
Design a DFA for strings that start with zero or more ‘b’s, followed by zero or more repetitions of ‘aaa’ or ‘bbb’, and end with ‘ba’
Regular Expression = b*(aaa + bbb)*ba
L = {ba, bba, bbaaaba, bbba, bbbbbbba, baaabbbba, …}
Some rejected strings = {a, b, bb, ab, aaa, bbb, baba, babba, abba, …}
Language contains all strings that:
-
Begin with any number of ‘b’,
-
May have repetitions of “aaa” or “bbb”,
-
And must end with “ba”
DFA for RE = b*(aaa + bbb)*ba is given below
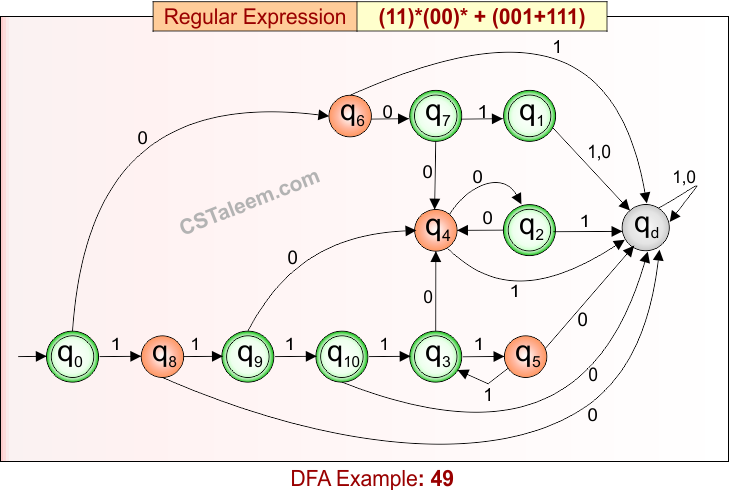
Deterministic Finite Automata: Example 49
Design a DFA for strings that are either:
-
Zero or more repetitions of “11” followed by zero or more repetitions of “00”,
-
OR exactly “001” or “111”
Regular Expression = (11)*(00)* + (001 + 111)
- L = {ε, 11, 00, 1100, 1111, 0000, 11110000, ……., 001, 111}
- Some rejected strings = {1, 0, 10, 100, 101, 11001, …}
DFA for RE = (11)*(00)* + (001 + 111) is given below
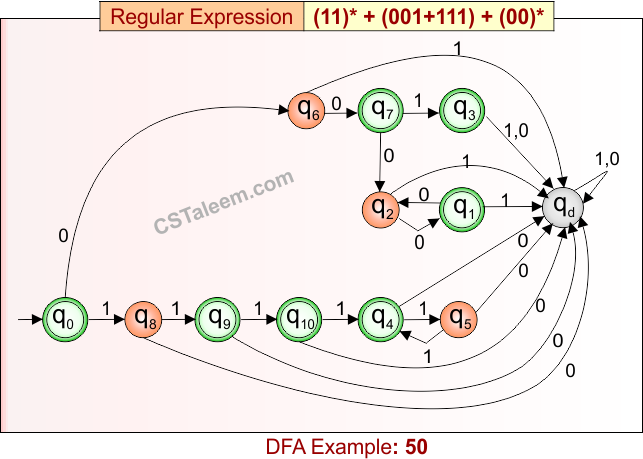
Deterministic Finite Automata: Example 50
Design a DFA for strings that are either:
-
Zero or more repetitions of “11”,
-
OR exactly “001” or “111”,
-
OR zero or more repetitions of “00”
Regular Expression = (11)* + (001 + 111) + (00)*
- L = {ε, 11, 1111, 111111, 00, 0000, 000000,…………., 001, 111}
- Some rejected strings = {1, 0, 01, 10, 100, 110, 011, 0011, …}
DFA for RE = (11)* + (001 + 111) + (00)* is given below
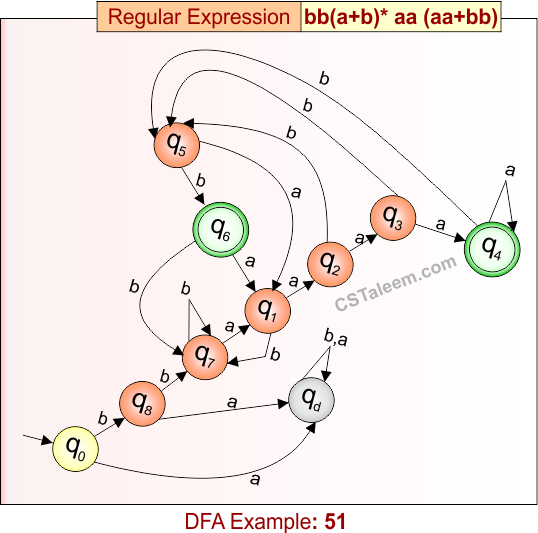
Deterministic Finite Automata: Example 51
Design a DFA for strings that start with ‘bb’, followed by any combination of ‘a’ or ‘b’, then ‘aa’, and end with either ‘aa’ or ‘bb’
- Regular Expression = bb(a + b)*aa(aa + bb)
- L = {bbaaabb, bbaaaaa, bbaaaa, bbabaaabb, bbbaabb, …}
- Some rejected strings = {bb, bbaa, bbaab, bbab, bbabaaa, bbaabbb, …}
Language contains strings that:
-
Start with “bb”,
-
Have any number of ‘a’ or ‘b’,
-
Then contain “aa”,
-
And end with either “aa” or “bb”
DFA for RE = bb(a + b)*aa(aa + bb) is given below
Applications of Deterministic Finite Automata
Here is the top 5 Applications of Deterministic Finite Automata (DFA):
1. Lexical Analysis in Compilers
-
Use: DFA is used by lexical analyzers (tokenizers) to recognize keywords, identifiers, operators, and symbols in source code.
-
Example: Recognizing
int,while,return, etc., from a stream of characters.
2. Pattern Matching / Text Searching
-
Use: DFA-based algorithms efficiently find occurrences of a pattern in a string.
-
Example: Searching for
abcin a long document using Knuth-Morris-Pratt (KMP) algorithm.
3. Network Protocols & Communication
-
Use: DFA models protocols where inputs (signals/packets) determine state transitions in communication systems.
-
Example: Handshake protocol in TCP/IP
4. Input Validation
-
Use: DFA can be used to validate user input or data format against specific rules.
-
Example: Checking if a string is a valid binary number or a date format (e.g.,
dd-mm-yyyy).
5. Control Systems / Robotics
-
Use: DFA models the logic of machines or systems that react to sequences of events.
-
Example: A vending machine accepting a sequence of coins and dispensing items based on input sequence.