Dependency Preserving Decomposition
As we know, table decomposition should be either lossless or dependency-preserving to avoid the loss of data. So, According to dependency preserving,
The decomposition of relation R with FD’s (F) into relation R1 and R2 with their FDs (F1) and (F2) respectively, will be dependency preserving if.
Closure of F (F+) = Closure of F1 (F1+) U Closure of F2 (F2+)
The above equation can be explained as
“If a relation R is decomposed into relation R1 and R2, then the dependencies of R either must be a part of R1 or R2 or must be derivable from the dependencies of R1 and R2.”

Note: After the Union of R1 and R2 attributes, the Resultant must be equal to attributes of the original relation R.
Some more Explanation is here,
Hidden Dependencies
Some dependencies are directly given, but some dependencies are derived from other dependencies. So, these derivable dependencies are known as hidden dependencies. Let’s explain with an example.
- Suppose a relation R(A,B,C,D)
- Give FD’s = A→B, B→C
- From the given dependencies, we can drive FD=A→C.
- So, dependency (A→C) is a hidden dependency.
Dependency Preserving Example
Let’s explain the dependency preserving with an example
Suppose a relation R with A, B, C, and D, and its FDs are A→B, B→C. This Relation R is decomposed into tables R1 with A and B attributes, R2 with B and C attributes, and R3 with B and D attributes.

Solution
1. First of all, Find the closure of each attribute given on the left-hand side of the given FDs of Relation R(ABCD). As given in the following diagram.

2. Second, Find all Non-Trivial FDs of Decomposed Relations (R1, R2, and R3) as given below.

3. Third, find all those Non-trivial FDs that are not determined from the given Relation R(ABCD). Let’s check one by one all Non-Trivial FDs of all decomposed relations R1, R2, and R3.
i. Check (A→B):
As A→B of Relation R1(AB) is directly given in the FDs of Relation R(ABCD). So, this Dependency can be determined from the original table R(ABCD). Because the Closure of A in the Original Table can determine “B”. So, this is a valid Dependency.
ii. Check (B→A):
As B→A of Relation R1 (AB) is not directly given in the FDs of Relation R(ABCD). This Dependency cannot determined from the FDs of the original table R(ABCD). Because the Closure of B in the Original Table cannot determine “A”. So, this is a valid Dependency.
iii. Check (B→C):
As B→C of Relation R2(BC) is directly given in the FDs of Relation R(ABCD), this Dependency can determined from the original table R(ABCD). Because the Closure of B in the Original Table can determine “C”, this is a valid Dependency.
iv. Fourth Check (C→B):
As C→B of Relation R2(BC), it is not directly given in the FD’s of Relation R(ABCD). But this Dependency can determined from the original table R(ABCD) Because the Closure of C in the Original Table can determine “B”. So, this is a valid Dependency.
v. Fifth Check (B→D):
As B→D of Relation R3(BD) is not directly given in the FDs of Relation R(ABCD), But this Dependency can determined from original table R(ABCD) Because Closure of B in the Original Table can determine “D”. So, this Dependency is valid.
vi. Sixth Check (D→B):
As D→B of Relation R3(BD) is directly given in the FDs of Relation R(ABCD). So, this Dependency can be determined from the original table R(ABCD) Because the Closure of D in the Original Table can determine “B”. Thus, this is also a valid Dependency.
So, above all, Non-trivial FD’s are valid except the 2nd FD (B→A), As in the following diagram
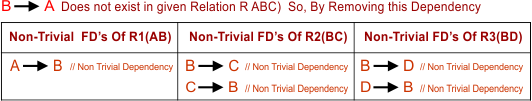
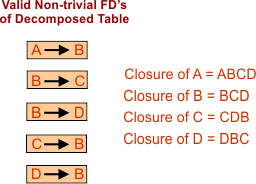
4. Find the closure of all valid Non-trivial FDs of Decomposed Relations (R1, R2, and R3) as given below
5. If all dependencies of a given relation are preserved through all valid non-trivial dependencies of its decomposed tables. Then, the original table will also be preserved.
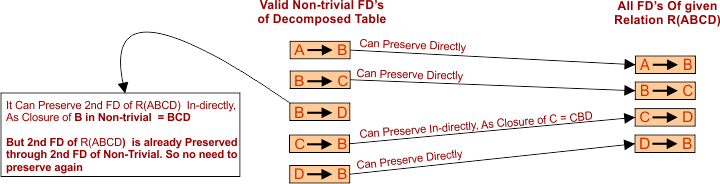
Explanation of the Above diagram
We will check all valid Non-trivial FDs of decomposed tables (one by one) and see whether these FDs can preserve all FDs of the original Relation. If it is preserved, then the decomposition is dependency preservation; otherwise, it is not.
All four FDs of original Relation are preserved through valid Non-trivial FDs No, 1,3,4, and 5. So, it is a dependency-preserving decomposition













