Extended Operators in Relational Algebra
Extended operators are those operators which can derive from other operators, i.e. (Unary or Binary operators).
Types of Extended Operators
There are 3 types of extended operators in Relational Algebra
- Intersection Operator
- Divide Operator
- Join Operator

1. Intersection Operator (∩)
The intersection operator is the reverse of the Union operator. So, this Operator can derive from the Union Operator. This operator can be defined as follows.
Let A and B be two relations.
Then
- A∩ B is the set of all tuples belonging to both A and B.
- In A∩ B, duplicates are automatically removed.
- Intersection operation is both commutative and associative.
Example
Consider the following two relations: A and B
Relation A
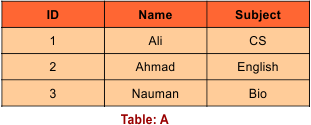
Relation B

Then, A ∩ B is

2. Division Operator (÷):
The division operator (X÷Y) can apply if and only if:
- Attributes of Y is a proper subset of Attributes of X
Proper Subset:
A={1,2,3} is a proper subset of B ={1,2,3,4} because the element 4 is not in the first set A.}
- After the division operation, the Remaining attributes in the table will be = (All attributes of X – All Attributes of Y).
- After the division operation, the Relation will return those tuples from relation X, which are associated with every tuple of Y.
Consider the following two tables: STUDENT_SPORTS and SPORTS
Table: STUDENT_SPORTS

Table: SPORTS

After applying division operator (STUDENT_SPORTS÷ SPORTS)
- The division operation can apply as attributes in the SPORTS table are a proper subset of attributes in the STUDENT_SPORTS table.
- The Result After the division operation, the Remaining attributes in the first table will be {ROLL_NO, SPORTS}-{SPORTS}=ROLL_NO.
- The Roll_No column of the Student_Sports table will have those values that are associated with all Y’s tuple {Hckey, Cricket}. ROLL_NO 1,2 are associated with Hockey only. ROLL_NO 3 is associated with all tuples of Y (Hockey and cricket). So, the resulting table will have the value “3” in the Roll_No column.
3. Join Operations:
A Join operation combines related tuples from different tables. Join operators can apply if and only if a given join condition is satisfied. Join operator denoted by ⋈.
For join operation, there must be some commonality in the two tables. As in the below tables, EMP_ID is common in both tables.
Join operation is used when we need to access data from more than one table.
In the following tables, we need Emp_Name and EMP_Salary. So it requires to join the EMPLOYEE and SALARY tables.
Example: Suppose EMPLOYEE and SALARY Tables
Table: EMPLOYEE
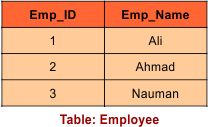
Table: SALARY

Apply Join Operation (EMPLOYEE ⋈ SALARY)
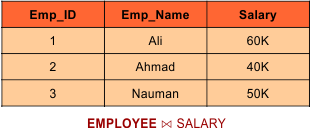
Types of JOIN Operator
- Natural JOIN
- OUTER JOIN
- LEFT OUTER JOIN
- RIGHT OUTER JOIN
- FULL OUTER JOIN
- Equi JOIN
In the next lecture, we will cover all the above Types of Joins.














