Introduction To DBMS

Data Modeling

Cardinality and Modality in ER Model

Participation Constraints in ER Model

Introduction to Relational Algebra

Unary Operators in Relational Algebra

Binary Operators in Relational Algebra

Extended Operators in Relational Algebra

Candidate vs. Super Key AND Prime vs. Non-Prime Attributes

Important Points of Normal Forms

Dependency Preserving Decomposition

Decomposition Without Dependency Preserving

Equivalence of Two Sets of FD’s

Conflict in DBMS | Expert Guide

Types of Recoverable Schedules

Serial Vs. Non-Serial Schedules

Concurrency Problems In Database

Lock Based Concurrency Control Protocol

Categories of Two Phase Locking

Conflicts in Timestamp Protocol

Timestamp Ordering With Examples

Conflict Serializability

Conflict serializability is used to check whether the given non-serial schedule is Serial or not. In conflict serializability,

we check conflict pairs and draw a precedence graph from a given schedule.
If the derived precedence graph from the schedule holds no loop, then that schedule will be a serial schedule.

Keep in mind a serial schedule will always be Serializable and Consistent.

Example of Conflict Serializability

Let’s explain the topic of conflict serializability with an example

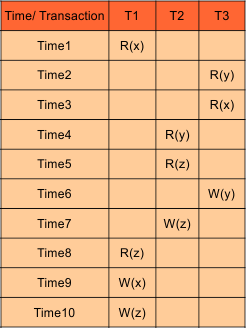
Problem: Check if the following schedule given in the diagram is serializable or not.

Solution:

R(x) means Read operation on data “x”
W(y) means Write operation on data “y”
So, x,y is data, and R, W are read and write operations

First, find the precedence graph from the above schedule. To draw a precedence graph,

Taking all transactions as the vertex.
Draw some arrows/edge based on conflict pairs in other transactions.

Steps to draw precedence graph

At time1, R(x) belongs to T1 exists, as a conflict of R(x) is W(x). so Check W(x) in T2 and T3. As No W(x) exists in T2 and T3, after time1. So, No edge is drawn from T1 to T2 or T3.
At the time 2, R(y) belongs to T3, as a conflict of R(y) is W(y). so Check W(y) in T2 and T1. As No W(y) exists in T2 and T1, after time2. So, No edge is drawn from T3 to T1 or T2.
At time 3, R(x) belongs to T3 exists, as a conflict of R(x) is W(x). so Check W(x) in T2 and T1. As W(x) exists in T1, after time3. So, an edge is drawn from T3 to T1.
At time 4, R(y) belongs to T2 exists, as a conflict of R(y) is W(y). so Check W(y) in T1 and T3. As W(y) exists in T3, after time4. So, an edge is drawn from T2 to T3.
At time 5, R(z) belongs to T2 exists, as a conflict of R(z) is W(z). So, Check W(z) in T3 and T1 after time 5. As a W(z) exists in T1, after time5. So, an edge is drawn from T2 to T1.
At time 6, W(y) belongs to T3 exists, as a conflict of W(y) is R(y) and W(y). so Check R(y) and W(y) in T2 and T1, after time6. No R(y) and W(y) exist in T2 and T1 after time 6. So, No edge is drawn from T3 to T1 or T2.
At time 7, W(z) belongs to T2 exists, as a conflict of W(z) is R(z) and W(z). so Check W(z) and R(z) in T1 and T3, after time7. As a W(z) exists in T1, after time7. So, an edge is drawn from T2 to T1. This edge already exists.
At time8, time9, time10, operation of T1 R(z), W(x), W(z) are executed respectively. Because after time 8, no operation of T2 and T3 exists.

After all time execution, the following precedence graph will be drawn which contains No loop.

Note: In the loop if we move from any edge, we will return to that edge without any problem.

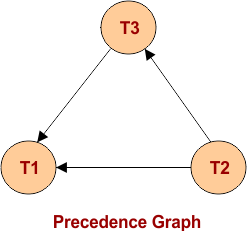
precedence graph in Conflict serializability

If the precedence graph has no loop or acyclic graph, the given schedule will be Conflict serializable and it will always be consistent.