Second Normal Form (2NF)
Before to learn 2NF, 3NF, BCNF, 4NF and 5NF you must know about
A table will be in 2NF if it follows the following
- The table should be in the First Normal form (1NF).
- There should be no Partial Dependency in the relation, it means all the non-prime attributes should be fully functional and dependent on the candidate key.
- The non-prime attribute never determines the non-prime attribute
Partial dependency: A part of the candidate key determining the non-prime attribute is called partial dependency. Suppose AB is the candidate key if a part of the candidate key (i.e., A) determines the non-prime attribute (i.e., X). Like A → X, then it is partial dependency.
Question Point of View for 2NF
If the following conditions exist, then the table will not be in 2NF.
1. According to partial dependency, L.H.S should be the proper subset of Candidate key, and R.H.S should be a non-prime attribute. (proper subset never be equal to actual candidate key)
2. Non-prime attribute determining non-prime attribute
Note: Prime attribute can determine Prime attribute, Prime can determine non-prime attribute, Non-prime can determine prime attribute, but non-prime can never be determined by non-prime attribute
Explanation of 2NF with FD Rules
Question: Consider a relation R= (ABCDEF) and Function Dependency FD = (C→F, E→A, EC→D, A→B). Check whether the given Relationship is in 2NF or not.
Solution:
- First, find Candidate key (C.K) = (EC)
- Second, find Prime attributes = (E,C)
- Third, find Non-Prime attributes = (A, B, D, F)
Now check for 2NF through every FD.
- First FD in Relation = C→F (As Partial dependency exists (L.H.S of FD is subset of candidate key and R.H.S is non-prime should not determine the non-prime attribute) so this FD is not suitable for 2NF)
- Second FD in Relation = E→A (Partial dependency exists, so this FD is not suitable for 2NF)
- Third FD in Relation = EC→D (No partial dependency exists so this FD is suitable for 2NF)
- Fourth FD in Relation = A→B (Non-prime determining non-prime attribute So, this FD is not suitable for 2NF).
Result: As all FDs of Relation do not fulfill the conditions of 2NF, this relation is not in 2NF.
Note: if any FD is not suitable for any normal form (i.e., 2NF), then that table will not be valid for that normal form.
Explain 2NF with a Relational Table.
Suppose a Customer table where attributes are Customer_ID, Store_ID, and Location.
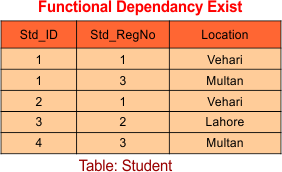
In the above-said table,
- Candidate key: Customer_IDStore_ID So,
- Prime attributes: Customer_ID, Store_ID
- Non-prime attributes: Location
Note that Store_ID determines the Location in the table, which is a partial dependency. Because a part of the candidate key is determining the attribute “Location.” So, the above relation is not in 2NF.
Solution: Divide the above table into two parts as given below,

Now note that both tables above fulfill the conditions of 2NF.













