Third Normal Form (3NF)
A table will be in the third normal form (3NF) when,
1. It is in the Second Normal form. 2. And, it does not have Transitive Dependency.
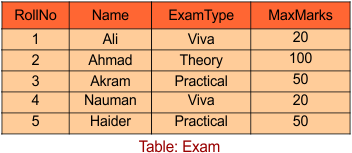
According to the transitive property, A determines B, and B determines C. So, “A” can determine C through B, but not directly. Let’s explain with a Relational table. In the following table, Roll_No is the candidate key, which determines ExamType, and ExamType determines the MaxMarks. So, the following table holds the transition property. That’s why it is not in 3NF.
Removal of Transitive Property
Transitive property can be removed by dividing the table into its parts. 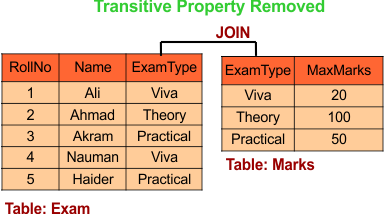
Let’s explain with a Functional dependency example
Conditions for Questions of 3NF
Any functional dependencies (FD) in relation will be 3NF if it fulfills the following condition.
L.H.S of FD should be a candidate or super key OR R.H.S of FD is a prime attribute.
Explanation of 3NF with FD Rules
Example 01:
Question: Consider a relation R =(ABCD) and FD= (AB→ C, C→ D). Check Relation is in 3NF or Not. Solution:
- CK ={ AB}
- Prime attribute ={ A, B}
- Non-prime Attribute= {C, D}
According to the first FD (AB→ C) . The L.H.S of FD contains the candidate key, so it is valid for the 3rd NF, according to the Second FD (C→ D). The L.H.S of FD is not a candidate key or supper key, And R.H.S is also a non-prime attribute. As both conditions were false, this FD is not valid for 3rd NF. Conclusion: As above, all FDs of a relation are not valid, So the relation is not in 3NF.
Example 02:
Question: Consider a relation R =(ABCD) and FD= (AB→CD, D→A). Check Relation is in 3NF or Not. Solution:
- First find Candidate key (C.K) = {AB, DB}
- Second Find Prime attributes = {A, B, D}
- Third Find Non-Prime attributes = {C}
Now check for 3NF
- For the first FD in Relation = AB→CD (As L.H.S contains the Candidate key, this FD is suitable for 3NF).
- For Second FD in Relation = D→A (As L.H.S does not contain the candidate or super key, but R.H.S contains the prime attribute, so this FD is suitable for 3NF.)
Result: As all FDs of Relation fulfill the conditions of 3NF this relation is in 3NF.













