Unary Operators in Relational Algebra
All those Operators that operate on a single operand are known as unary operators. There are various types of unary operators in relational algebra.
Types of Unary Operators
Unary operators are of three types
- Projection Operator
- Selection Operator
- Rename Operator
1. Projection Operator
- Projection Operator (π) displays the columns of a table based on the specified attributes.
- It just works on Columns
Syntax
π<attribute list>(R)
Attribute List contains single or multiple attributes
Example: Consider the following Student relation
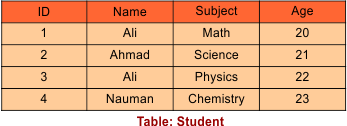
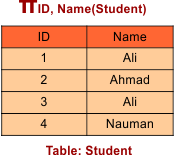
Then, we have the Result for Query πID, Name(Student)
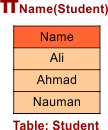
Result for Query πName(Student)
Note: This operator removes the redundancy if it is a single column. I.e., The Name “Ali” was twice in the same column (Name), and it was removed.
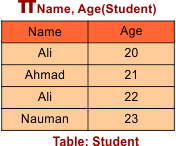
But in multiple columns, the name “Ali” becomes unique through other tuples, as in the below examples, and is not removed. As the First name “Ali” is age 20 and the other is age 22, both ”Ali” names are unique.
Result for Query πName, Age(Student)
2. Selection Operator
- Selection Operator (σ) performs a selection operation.
- It selects those rows or tuples from the table that satisfies the selection condition.
- It works with rows(tuples)
Syntax
σ<selection_condition>(R)
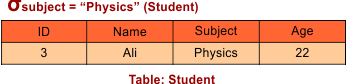
Query 1: Select tuples from a relation “Student” where the subject is “Physics.”
σsubject = “Physics” (Student)
The result of the above query from the Student table is given under,
Query: Select tuples from a relation “STUDENT” where the Name is “Ali” and the age is “20.”
σName = “Ali” ∧ age = “20” (STUDENT)
The result of above query from the Student table is given under,
Important Points of Selection Structure
Point-01:
- Along with the selection conditions, We may use logical operators (i.e. !, ∧ , ∨) and relational operators ( i.e., =, ≠ , <=, >, etc.).
- The projection operator is used to display the selected tuples.
Point-02:
- The selection operator always selects the entire tuple. So, It cannot select a part of a tuple.
Point-03:
- projection operator does not display the selected tuples.
Point-04:
- The selection operator follows the commutative property i.e., σ X ∧ Y (R) = σ Y ∧ X (R)
Point-05
- Rows selected by selection operation are always less than or equal to the number of rows in the original table.
So,
- Minimum Cardinality = 0
- Maximum Cardinality = |R|
3. Rename Operation (ρ)
- To rename relation, the rename operation is used, which allows us to rename the output relation
- .’Rename’ operation is denoted with rho(ρ).
Syntax:
ρ x (R)
Where the result of the current table with expression R is saved with the new table name of x.
Note: Through renaming operation we can rename the existing or new output table.
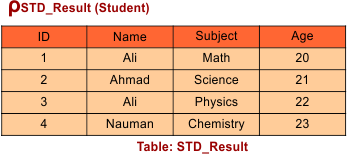
Example: Suppose the following “Student” table
Case 01: Change the name of a given table
To change the name of the above table to “STD_Result” Table: Student
Query syntax: ρ STD_Result (Student)
CASE 02: Change the Name of Output table
Select ID and Name from the “Student” table where the Subject is “Physics” and rename the output table to STD_Result as well.
Query syntax: ρ STD_Result (πID, Name (σsubject = “Physics” (Student)))
The output of the above query is given below,
CASE 03: Rename Output Table and its attributes
Select ID, Name from the “Student” table where the Subject is “physics” and
- Rename the output table to STD_Result
- Rename attribute ID, Name to STD_ID and STD_Name
Query syntax: ρ STD_Result (STD_ID, STD_Name) (πID, Name (σsubject = “Physics” (Student)))
Output of above query given under,
