Simultaneous Vs. Hierarchical Memory
In computer architecture, two basic methods are used to access the different levels of memory.
- Simultaneous Access Memory Organization
- Hierarchical Access Memory Organization
Notations
Some notations are used in this topic, details given below
Suppose,
- T1 = Access time of level L1·
- S1 = Size of level L1·
- C1 = Cost per byte of level L1·
- H1 = Hit rate of level L1
Same notations will be used for level L2 as (T2, S2, C2 and H2) and Same for Level 3.
1. Simultaneous Access Memory Organization
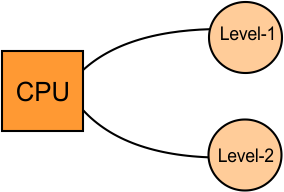
It is also known as an independent memory organization. In simultaneous access memory organization, All memory levels are directly connected with the CPU. Whenever the CPU requires any word, it searches in all the memory- levels simultaneously to find that particular word.
Example-01: Simultaneous Access Memory
When two memory –levels (L1 and L2) are directly connected to the CPU, then the average access time to any Word and cost per bit is given below
Average Memory Access Time
Average time required for accessing the memory per operation = H1 x T1 + (1 – H1) x T2
Note: The required searching word may definitely be present in the last level.· So, the hit rate for the last level is always 1.
Average Cost Per Byte
The average cost per byte of the memory = { C1 x S1 + C2 x S2 } / { S1 + S2 }
Example-02: Simultaneous Access Memory
When three memory –levels (L1, L2, and L3) are directly connected to the CPU, then average access time to any Word and cost per bit is given below

Average Memory Access Time
Average time required to access memory per operation = H1xT1 + (1 – H1) x H2 x T2 + (1 – H1) x (1 – H2) x T3
Average Cost Per Byte
The average cost per byte of the memory = { C1 x S1 + C2 x S2 + C3 x S3 } / { S1 + S2 + S3 }
2. Hierarchical Access Memory Organization
In hierarchical memory organization, all memory levels are connected with each other in a sequence, as explained below.
- Level 1 is directly connected to the CPU.
- Level 2 is directly connected to Level 1.
- and Level 3 is directly connected to Level 2 and so on.
Whenever the CPU requires any word, then
- It searches for the required word first in level 1, and if it’s not found, then it looks for it in the next level (level 2).
- In the same way, If the required word is not found in level 2 then CPU moves to next (level 3) and so on.
Example-01: Hierarchical Access Memory
When two memory levels (L1 and L2) are connected to the CPU in a hierarchical fashion. The average access time to any Word and cost per bit, shown

Average Memory Access Time:
Average time required to access memory per operation = H1 x T1 + (1 – H1) x (T1 + T2)
Average Cost Per Byte-:
Average cost per byte of the memory = { C1 x S1 + C2 x S2 } / { S1 + S2 }
Example-02: Hierarchical Access Memory
When three memory levels (L1, L2, and L3) are directly connected to the CPU in a hierarchical fashion. Then, the average access time to any Word and cost per bit, are given below

Average Memory Access Time:
Average time required to access memory per operation = H1 x T1 + (1 – H1) x H2 x (T1 + T2) + (1 – H1) x (1 – H2) x (T1 + T2 + T3)
Average Cost Per Byte:
The average cost per byte of memory = { C1 x S1 + C2 x S2 + C3 x S3 } / { S1 + S2 + S3 }
PRACTICE Questions BASED ON MEMORY ORGANIZATION
Question Number 1:
Consider a system with 2-level caches. Access time of L1, L2, and Main memory are 1ns, 10ns, and 500ns. The hit ratios of L1 and L2 are 0.8 and 0.9. What is the average access time of the system ignoring search time within the cache?
Solution: As mentioned in the question, ignore the search time in the cache. So, it is independent memory organization because we cannot ignore the search time at any level in hierarchical memory organization. So
Average Access Time = H1T1 + (1-H1) H2T2 + (1-H1)(1-H2)T3
=0.8×1 + (0.2) x0.9×10 + (0.2)(0.1)x500
=12.6ns
Note: If the memory organization method is not mentioned in the question, first try the independent method to solve the problem.
Question Number 2:
Find the average memory access time when the cache hit rate is 70%, cache access time is 10 ns, and the main memory access time is 200 ns through the following cases
- Independent memory organization.
- Hierarchical access memory organization
Solution
Case-01: Independent Memory Organization

Average memory access time
= H1 x T1 + (1 – H1) x T2
= 0.7 x 10 ns + (1 – 0.7) x 200 ns = 7 ns + 0.3 x 200 ns = 4 ns + 60 ns = 64 ns
Case 02: Hierarchical Access Memory Organization

Average memory access time
= H1 x T1 + (1 – H1) x (T1 + T2)
= 0.7 x 10 ns + (1 – 0.7) x (10 ns + 200 ns) = 7 ns + 0.3 x 210 ns = 4 ns + 63 ns = 67 ns
Question Number 03:
Let’s suppose a computer has a cache, main memory (RAM), and a hard disk used for virtual memory. Access to the cache takes 1 ns, access to the main memory takes 10, and access to the disk takes 1000 ns. Suppose the hit ratio of the cache is 0.9, and the main memory is 0.8. The effective access time required to access a referenced word on the system is the case when
- Simultaneous access memory organization is used.
- Hierarchical access memory organization is used.
Solution
Part-01:Simultaneous Access Memory Organization-

The memory organization will be as shown-
Effective memory access time
= H1 x T1 + (1 – H1) x H2 x T2 + (1 – H1) x (1 – H2) x H3 x T3
= 0.9 x 1 ns + (1 – 0.9) x 0.8 x 10 ns + (1 – 0.9) x (1 – 0.8) x 1 x 1000 ns = =?
Part-02: Hierarchical Access Memory Organization-
The memory organization will be as shown-

Effective memory access time
= H1 x T1 + (1 – H1) x H2 x (T1 + T2) + (1 – H1) x (1 – H2) x H3 x (T1 + T2 + T3)
= 0.9 x 1 ns + (1 – 0.9) x 0.8 x (1 ns + 10 ns) + (1 – 0.9) x (1 – 0.8) x 1 x (1 ns + 10 ns + 1000 ns) =?













