Intro to COA

K-way Set Associative Mapping

It is a mixture of Direct and Fully associative mapping.

K-way Set Associative Mapping- Example

  • Total No. of Set= Total No. of lines/K
  • Here, K is K-way Set Associative
  • For a 2-way set associative (K=2)
  • Total No. Of Set = 4/2 = 2 sets (S0, S1)

Which block will be in which line? It Is calculated by the formula K MOD N. Here, “K” is the Block Number, and “N” is the Total number Set in the Cache.

For example

  • If Block No =0, then (0 MOD 2) = 0. It means Block 0 will be in Set 0.
  • and If Block No =7, then (7 MOD 2) = 1. It means Block 7 will be in Set 1.
  • and If Block No =10, then (10 MOD 4) = 0. It means Block 10 will be in Set 0.

So,

The one of the following block will be in set zero (S0) in any line L0 or L1 at a time.
B0, B2, B4, B8,……,B28, B30
The one of the following block will be in set one (S1) in any line L2 or L3 at a time.
B1, B3, B5, B7,………. ,B29, B31

Physical Address

When the Cache has 4 lines and considers a 2-way set associative

K-way Set Associative (block and block offset format values)

Searching for a block through Tag (Cache Hit or miss)

Suppose the CPU generates an address 0011000 for 128-word main memory.

The first two bits (00) represent the Block offset, and the next bit (0) represents the set number. The last four bits (0011) represent the Tag in Cache memory.

The tag bits of the CPU address do not match the tag bits of any line of Set S0. So, it is a cache miss case.

K-way Set Associative Mapping-Explain-with-Example-Cache Hit or miss

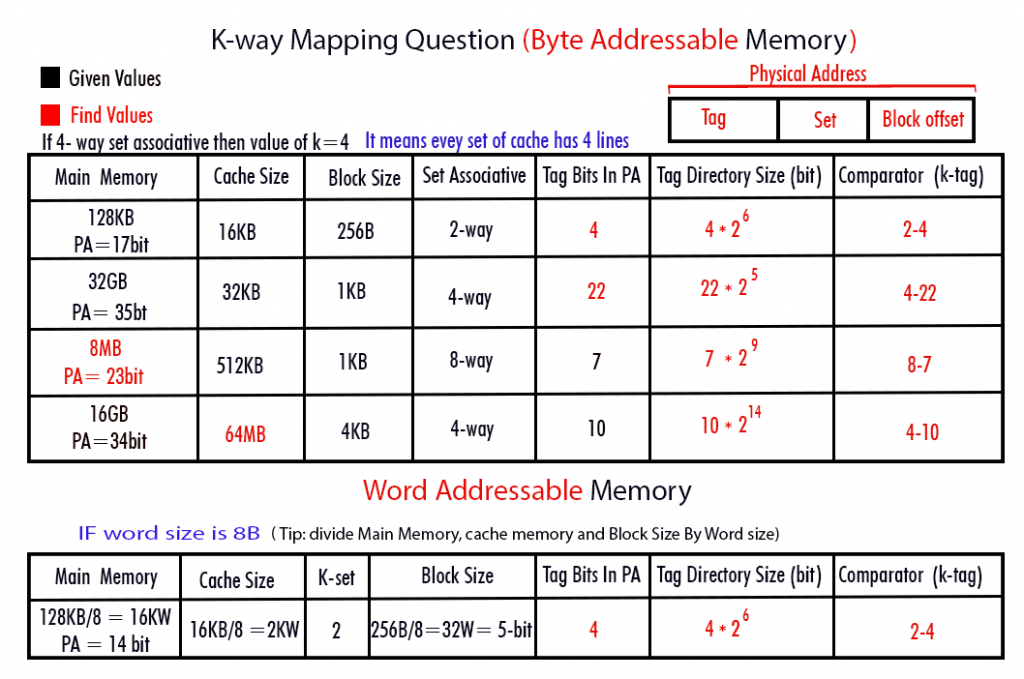
Numerical Problems

Formulas for K-way

  • Physical address = Tag + set +block offset
  • Comparator value in k-way set associative is = (k-value) – (tag bit). e.g. (7-8) means that 7 lines of a set are compared with 8 bits of tag.

Q1. If the cache size is 64KB and the Block/line size is 8B, how many bits are required to represent lines of 4-way set associative cache memory?

Total lines = Cache size/ Block size = 64KB/8B = 213B

So 13 bits are require to represent lines in cache.

Total bits for set = Total lines / K-way = 213B/22 = 211

So 11 bits are require to represent sets in cache.

Q2. If we find 10 bits for Set in a 4-way set associative and block size is 16 kb, Then the Cache size will be.

Cache size in K-set associative = total set * total lines per set * line size

Cache size = 210  *4* 214 B= 64 MB.

Problem 01:

K-way Set Associative (Byte and Word addressable) Numaricals

Problem 02: A 4-way set associative cache memory with a capacity of 16KB is built using a block size of 8 words. The word length is 32 bits. The size of the physical address space is 4GB. Find the no of bits for the Tag field.

Block size = 8×4 Bytes = 32 B = 25B

No of Sets in Cache = Size of Cache/ Block Size* K-way = 4KB/25B*4 = 27B

Physical Address Space = 4GB = 232 B

So According to Formula

Physical Address space = Tag + Total no. of sets + Block Size

232 B = Tag + 27B + 25B

Tag = 220B

So, 20 Bits are require to represent the tag number

Advantages and Disadvantages

Advantage: Comparison time is reduced as compared to fully associative

Disadvantage: Some Conflict miss factors involved.

Example: A person who has to live in one room is direct mapping. It is straightforward to find him. But there is a restriction for him not to move anywhere. Fully associative means a person can live anywhere in Pakistan, so searching time is increased, but the restriction is removed, and K-way tells us a person can live in one state in the country.