Simplify Boolean Expressions Using K-MAP
The K-Map method is a simple and efficient method for simplifying Boolean Expressions. In this lecture, we will learn to solve two and three variables Boolean functions using K-MAP. This method is also known as the Karnaugh Map.
K-MAP is represented in the form of a Truth Table. In a truth table, a function of n variables will have 2^n min-terms. For example, there will be four min-terms for two variables, i.e.(x,y), and 8 min-terms for 3 variables.
Note: Min-terms and Max-terms are forms of Literals.
Two-Variable K-Map
The 0 and 1 represent the row and column. X and Y are variables of a Boolean function. The following diagram shows the arrangement of two variables of the Boolean function in the form of K-MAP.
- According to Pic A, the Square in Row 0 and Column 0 is m0. Square in Row 0 and Column 1 is m1. M0, m1, m2… m (n) are the min-terms.
- According to Pic B, the Square in Row 0 and Column 0 is X’.Y’ and so on.

Example 01: Simplify the Boolean Function F(X, Y) = x.y+x’y
Step 01: Represent the function in the form of K-MAP
Represent the corresponding boxes of (x.y) and (x’.y) with 1 and the remaining with 0.

Step 02: Mark any group of two or for adjacent 1 as shown below

Step 03: write a simplified expression for each group
X’.y+x.y = (x’+x).y = 1.y =y
Step 04: write the final simplified form as a sum of products
F(X, Y) = y
Example 02: Simplify the Boolean Function F(X, Y) = x.y’+x’.y+x.y
Step 01: Represent the function in the form of K-MAP
Represent the corresponding boxes of (x.y’), (x’.y), and (x.y) with 1 and remaining with 0.

Step 02: Mark any group of two or for adjacent 1 as shown below

Step 03: write a simplified expression for each group
Group 01: X’.y+x.y = (x’+x).y = 1.y =y
Group 02: X.y’+x.y = (y’+y).x = 1.x =x
Step 04: write the final simplified form as a sum of products
F(X, Y) = x+y
Example 03: Simplify the Boolean Function F(X, Y) = x’.y’+ x.y’+x’.y+x.y
Step 01: Represent the function in the form of K-MAP
Represent the corresponding boxes of (x’, y’),(x.y’), (x’.y), and (x.y) with 1 and remaining with 0.

Step 02: Mark any group of two or for adjacent 1 as shown below
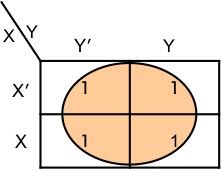
Step 03: write a simplified expression for each group
All boxes are filled with one, so there will be only one group.
Group 01: x’.y’+ x.y’+x’.y+x.y = y’(x+x’)+ y(x+x’)= y’.1+y.1= y’+y = 1
Step 04: write the final simplified form as a sum of products
F(X, Y) = 1
Three-Variable K-Maps
There are eight min-terms in a three-variable map. Therefore, the map consists of eight squares.

Using the K-Map method, let’s explain some examples of three-variables Boolean algebra simplifications.
Example 01: Simplify the Boolean Function F(X, Y, Z) = x.y.z’+ x’.y’.z’+ x.y’.z’+x’.y.z
Step 01: Represent the function in the form of K-MAP
Represent the corresponding boxes of x.y.z’, x’.y’.z’, x.y’.z’, and x’.y.z with 1 and remaining with 0.
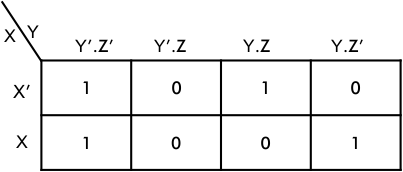
Step 02: Mark any group of two or for adjacent 1 as shown below

Step 03: write a simplified expression for each group
Group 01: x’.y’.z’ + x.y’.z’ = y’.z’(x+x’) = y’.z’(1)= y’.z’
Group 01: x.y’.z’ + x.y.z’ = x.z’(x+x’) = x.z’(1) = x.z’
Step 04: write the final simplified form as a sum of products
F(X, Y) = y’.z’+ x.z’













