Direct Mapping
In Direct Mapping, each block of main memory is mapped to a specific line in the cache.
When determining which block is in which line, the formula K MOD N is used because the block size is equal to the line size. where “K” is the Block Number and “N” is the Total number of lines in the Cache.
For example
- If Block No =0, then (0 MOD 4) = 0. It means Block 0 will be in Line 0.
- and If Block No =7, then (7 MOD 4) = 3. It means Block 7 will be in Line 3.
- and If Block No =10, then (10 MOD 4) = 2. It means Block 10 will be in Line 2.
So,
The one of the following block will be in Line zero (L0)
B0, B4, B8, B12, B16, B20, B24, B28
The One of the following blocks will be in Line zero (L1)
B1, B5, B9, B13, B17, B21, B25, B29
The One of the following blocks will be in Line zero (L2)
B2, B6, B10, B14, B18, B22, B26, B30
The One of the following blocks will be in Line zero (L3)
B3, B7, B11, B15, B19, B23, B27, B31
Address Mapping from RAM to Cache
Let suppose there is a Main Memory (RAM) of size 128 Words and a Cache of size 16 Words. Main Memory and Cache are divided into blocks and Lines, respectively. The size of each block Line is 4- words, as shown in the following diagram.

To represent 32 blocks, 5-bits are required. And To represent 4-words in the block offset, 2-bits are required. And To represent 4 lines in cache memory, 2 bits are required.

For Example, if an address of Word 0 of block 22 in the main memory is (1011000) given below

Where,
Block offset: Represent Block size
Block No: Represent Total No of Block In main memory
Line No: Represent Total No. of Lines in Cache
Tag: Represent possible Blocks in each Line
Tag Explanation: There are 32 blocks in the main memory. So, only 8 blocks can come in L0, 8 Blocks in L1, 8 Blocks in L2, and 8 Blocks in L3, but one block in one line at a time. So, to represent 8 blocks for each line, only 3 bits are required.
Note: if there are 8 words, then 3 bits are required for block offset.
Searching for a block through Tag (Cache Hit or miss)
Suppose the CPU generates an address 0010100 for 128-word main memory. The first two bits (00) represent the Block offset, the next two bit (01) are used to represent the Block number, and the last three bits (001) represents the Tag in Cache memory.
To find the Particular block in cache memory
- First, find the line where the required Block is present in cache memory
- Second, Compare the tag bits of the generated address with the tag bits of the line where the actual Block is present. If it matches, then Cache Hit; otherwise, cache miss.
Note: Only one comparator is required in direct mapping to find cache hit or miss. As we know the exact block through K MOD N formula. We match the tag of the given address with the tag of a particular cache line only Once. So, the Comparator value in direct mapping is always one.
Explain with an Example: For address 0010100 in the following diagram; it is a cache, Hit. But if the address is 1010011, then it is a cache miss because the last three Tag bits (101) are not found in the tag bits of cache lines.

Note: if the cache misses, then we replace the block of that line (in cache) with the required block (from main memory)
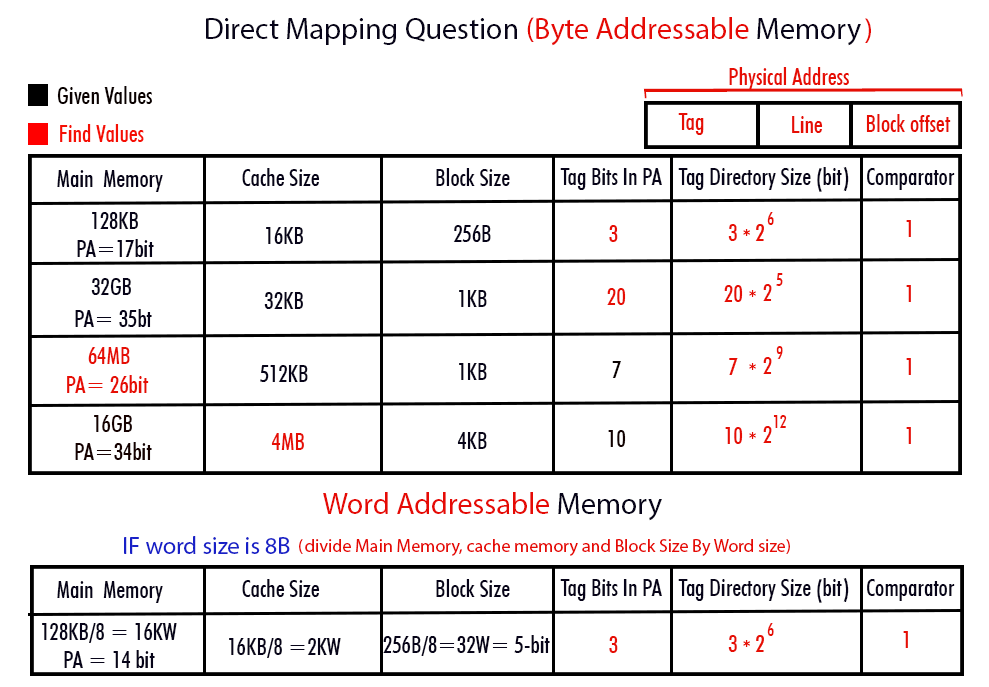
Numerical: Physical address
Q1: If the memory size is 128 KB and memory is Byte addressable, then how many bits are required to represent the Physical address of the main Memory
128KB = 217B
So, 17 bits are required for the physical address (PA) of the main memory
Q2: If the memory size is 128 KB, memory is word addressable, and the word size is 8 bytes, then how many bits are required to represent the Physical address of the main Memory?
128KB/8B = 214B
So, 14 bits are required for the physical address (PA) of the main memory
Block Offset / Line Offset
Q3: If we have 8 words in the block and each word is f 32-bit, how many Bits are required for Block offset? Main memory is byte-addressable
Total words * size of word in bytes = 8*4= 32= 25B
So, 5 bits are required for Block Offset/Line offset
Q4. If we have 8 words in the block and each word is f 32 bit, then how many
Bits required for Block offset. Main memory is word addressable
Total words = 8 = 23B
So, 3 bits are required for Block Offset/Line offset
Cache Lines
Q5. If the cache size is 64KB and the Block/Line size is 8B, then how many
bits are required to represent lines of cache memory
Total lines = Cache size/Block size = 64KB/8B = 213B
So, 13 bits are required to represent lines in the cache
Q6. if we have PA, Block Offset, and Line Bits, then we can calculate
Tag through the following equation in Direct Mapping
Physical Address (PA) = Block Offset + Line + Tag
Shortcut Formula’s
- Cache memory = total bits for line representation+ total bits for block offset
- Tag bits for direct mapping= size of main memory/cache memory
- Tag Directory = tag bits * total no. of lines
- Comparator = 1
Problem 01: Consider a directly mapped cache of size 32 KB with a block size of 32 bytes. The CPU generated 32-bit addresses. Find the number of bits required for cache indexing and tag bits, respectively.
Block Size = 32B = 25 B (5 bits are used for Line or Block offset)
Cache size = 32 KB
Total cache lines = Cache size / Block size = 32KB/32B = 210B (so 10 bits are required for cache indexing or cache lines)
As we know
Physical Address (PA) = Tag + Line + Block Offset
32 bit = Tag + 10bit + 5bits
Tag = 32-10-5 = 17bits
Problem 02:
Advantages
The advantage of direct mapping is that the Checking of cache Hit or Miss is very simple in the Direct Mapping method. If we have the physical address of a word, then we go to that word line number in the Cache and compare the Tag of this word and the cache line tag. If both are similar, then the cache hit; otherwise, the cache misses.
Disadvantage
The disadvantage is conflict miss. We know that it is fixed for each block to come in a particular cache line. If Block (B1) is loaded in Line 1 and B5 comes. Then it replaces the B1 rather to move in other lines even if other lines are empty at that time.













