Pumping Lemma for Regular Languages
Pumping Lemma is applied to infinite languages to show that languages are not regular. It should never be used to prove that a language is regular. That’s why the pumping lemma is also called a negative test. A simple description of the pumping lemma is given in the following diagram.

| V. Important:
Point 01: Keep in mind that all finite languages are regular, and there is no need to check whether they are regular or not, but all infinite languages may or may not be Regular. For example, as a^n, b^n is an infinite language but not a Regular language. So, the Pumping Lemma Test is important to check whether infinite languages are regular or not.
|
Main Methods to Determine if a Language is Regular
Although there are many methods to check whether the infinite languages are regular or not, the pumping Lemma is one of the most important.
| Method | Description |
|---|---|
| 1. Pumping Lemma | Used to prove a language is not regular by contradiction (using the “pumping property”). |
| 2. Myhill–Nerode Theorem | A powerful method that checks regularity based on the number of equivalence classes — finite ⇒ regular. |
| 3. Finite Automaton Construction | If you can build a DFA, NFA, or ε-NFA, then the language is regular. |
| 4. Regular Expression Existence | If a regular expression can be written for the language, it is regular. |
| 5. Closure Properties | Use known closure operations (union, concat, etc.) to build or break down a language into regular parts. |
| 6. State Minimization (DFA) | Helps in analyzing the DFA structure to determine regularity (used alongside Myhill–Nerode). |
Pumping Lemma For Regular Languages – Key Concept
The pumping lemma is used for only regular languages and context-free languages (with separate versions for each) to prove that a language is not regular or not context-free. In this class, we only discuss the pumping lemma for regular languages
Look at the following diagram
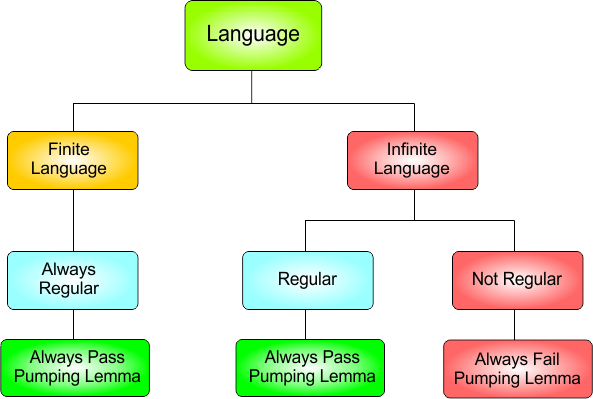
The above diagram says there are three cases with regular language
-
Case 01:If a language is finite, then it is regular and always satisfies the Pumping Lemma.
-
Case 02: If a language is infinite and regular, then it always satisfies the Pumping Lemma.
-
Case 03: If a language is infinite and non-regular, then it fails the Pumping Lemma.
In this lecture, we will discuss these 3 cases with various examples
Key Terminologies in Pumping Lemma For Regular Languages
Before explaining various key terminologies, let’s see how various variables that we are using in the pumping lemma are explained in the following diagram.
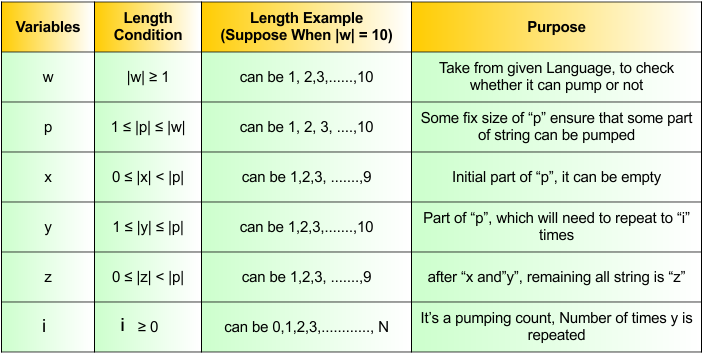
Let’s explain the main terminologies in the pumping lemma for regular languages
i. String “w” from Language
In general, a language can generate infinitely many strings (“w”) unless it is explicitly defined as a finite language. In the context of the pumping lemma, we always assume the language is infinite, because finite languages are always regular.
Example:
L = {an ∣ n≥0}
Strings (“w”) generated = {ϵ, a, aa, aaa, aaaa,…}
An infinite number of strings, used in pumping lemma discussions
ii. Magical Number “p”
The magical number (also called pumping length) is a fixed positive integer such that every string w in a regular language with ∣w∣ ≥ p can be split as w=xyz pumped (i.e., xyiz ∈ L where i≥0).
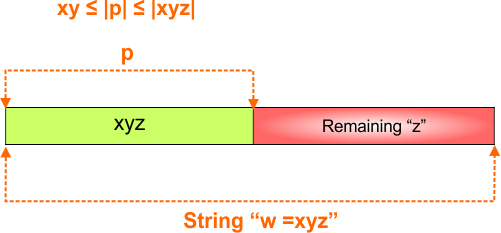
Note: Length of “x” and “z” can be “≥0″, but “y” and “p” must be “≥1″.
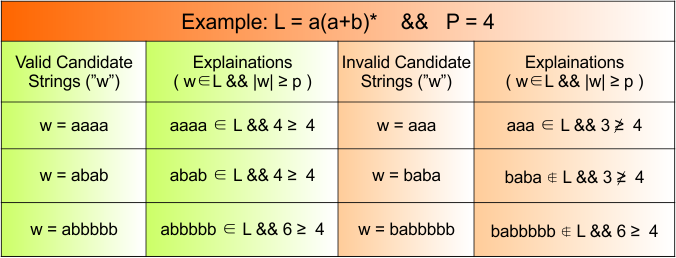
Example: L = {an ∣ n≥0}, Let p = 4
- Strings (“w”) generated = {ϵ, a, aa, aaa, aaaa,…}
- All those strings where string w ∈ L and ∣w∣ ≥ p are called candidate strings; shorter strings are ignored.
- Valid choices of strings “w” (candidate strings ) = {aaaa, aaaaa, aaaaaa,…}
- Invalid choices of strings “w” = { a, aa, aaa}
Important Note:
-
Minimum Pumping Length (magical number “p”) : The smallest positive integer p such that all strings w ∈ L with ∣w∣≥p| can be split as w=xyz and pumped is called Magical number.
-
For any language L, in the pumping Lemma if p = n is working, then p = n+1, n+2, n+3, …. also work with same logic of “y”.
- Find the Magical Number (P) by using Hit and Trial method. Once you become expert in pumping Lemma, you can Guess the Magical Number easily in the first sight of language.
iii. Candidate String
A candidate strings are those string that meets the following conditions
- w ∈ L
- |w| ≥ p
used to test whether the language satisfies the Pumping Lemma.
In simple words, it is a long enough string selected from the language to check if it can be pumped.
|
Problem in Candidate Strings: The Pumping Lemma says that if a language (L) is regular, then every candidate must be pumped. It is impossible to check all candidate strings manually because candidate strings can be infinite. Solution: We provide the general proof, which applies to all candidate strings, which proves all candidate strings can pump. We provide various examples in this lecture where “general proof” is given. |
Important: If even one candidate string out of “n” fails, then the language is not regular, where n≥1.
iv. Candidate String Division (“xyz”)
The following picture will help you to understand the division of every candidate string into three parts “xyz”.
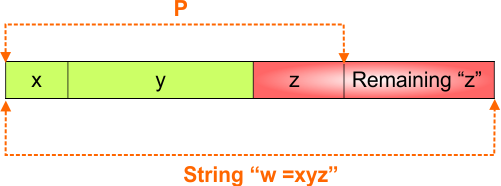
Example: L={an ∣ n≥0}, p=4
Choose a Candidate string: w=aaaa,
All possible divisions of the candidate string “w” are given below, which follow the following conditions
- w=xyz
- ∣xy∣ ≤p
- ∣y∣ ≥ 1
| x | y | z |
|---|---|---|
| ε | a | aaa |
| ε | aa | aa |
| ε | aaa | a |
| ε | aaaa | ε |
| a | a | aa |
| a | aa | a |
| a | aaa | ε |
| aa | a | a |
| aa | aa | ε |
| aaa | a | ε |
v. Repetition of “Y” in Candidate String Using “i”
“y” is the “repeating part” of the string, and “i” tells how many times y is repeated. For a regular language, all xyiz must remain in the language.
Example: L={an ∣ n≥0}, p=4
Choose a Candidate string: w=aaaa, where consider x = ε, y= aa, and z = aa, the repition of y is given below
| i | xy^i z | Resulting String |
|---|---|---|
| 0 | “” + “” + aa | aa |
| 1 | “” + aa + aa | aaaa |
| 2 | “” + aaaa + aa | aaaaaa |
| 3 | “” + aaaaaa + aa | aaaaaaaa |
Important Note:
- If some section of “y” does not work, then try some other section of “y” in the given string “w”. Pumping Lemma says that we need some section “y” which can be repeated and the result is inside L.
- Remember for different candidate strings, different “y” can work. So, different w’s can be pumped in different ways
Pumping Lemma Conditions for Regular Languages

If L is a regular language, then there exists a constant p (called the pumping length) such that every string w in L with length at least p can be divided into three parts
w = xyz
Such that
-
|y| ≥ 1
(y is not empty — it contributes something to the string) -
|xy| ≤ p
(The repetition part occurs within the first p characters) -
For all i ≥ 0, the string xyiz ∈ L
(i.e., you can “pump” y — repeat it any number of times — and the string stays in the language)
Pumping Lemma Algorithm for Infinite Regular Language
Here is a descriptive diagram for the pumping lemma algorithm
Step 1: Assume that the language L is regular. By the Pumping Lemma for regular languages, there exists a pumping length “p”, where p ≥ 1.
Step 2: Draw all possible strings from the given language.
Step 3: Choose a string w ∈ L such that |w| ≥ p
Step 4: Split the selected string into xyz. Consider all possible decompositions of the stringw = x y z ;such that the following conditions hold:
-
|xy| ≤ p -
|y| ≥ 1
(This ensures that x and y are within the first p symbols of w and that y is non-empty.)
Step 5:For each valid decomposition, check whether:
x yⁱ z ∈ L for all i ≥ 0
If there exists any value of i ≥ 0 such that: x yⁱ z ∉ L Then the pumping condition fails.
Step 06: Provide a general proof that all strings must pump at any “p” using the same logic of “y” by repeating steps 3, 4, and 5.
Step 7: If the pumping condition fails for every possible decomposition, then the pumping lemma is violated. So, L is NOT regular.Otherwise, if the pumping condition holds, no conclusion can be drawn about the regularity of L.
Note:
|
Pumping Lemma Algorithm for Finite Regular Languages
- Step 01: For a finite language L, the minimum pumping length is p = m+1, where m is the length of the longest string in L.
- Step 02: For a language L, if there exists a pumping length p such that no candidate string violates the pumping conditions, then L satisfies the pumping lemma.
Case 01 Examples: Pumping Lemma For Finite Regular Languages
All finite regular language satisfiy the pumping lemma. Here is two line algorithm proof
Example 01: L = {10}
Step 01: the Language given in example 01 is finite, because number strings are finite. The length of all strings is given below
- Length of string (“10”) = 2
The maximum length of any string in the given language is 2. So, pumping length p will be 2+1 = 3
Step 02: If p = 3, no candidate string is found, as no candidate string exists; hence, nothing violates the pumping conditions. Hence, L satisfies the pumping lemma.
Example 02: L = {10, 1111, 010101, 11110000}
Step 01: the Language given in example 02 is finite, because number strings are finite. The length of all strings is given below
- Length of string (“10”) = 2
- Length of string (“1111”) = 4
- Length of string (“010101”) = 6
- Length of string (“11110000”) = 8
The maximum length of any string in the given language is 8. So, pumping length p will be 8+1 = 9
Step 02: if p = 9, no candidate string is found, as no candidate string exists; hence, nothing violates the pumping conditions. Hence, L satisfies the pumping lemma.
Example 03: L = {10, 1111, 010101, 11110000, 1111100000}
Step 01: the Language given in example 03 is finite, because number strings are finite. The length of all strings is given below
- Length of string (“10”) = 2
- Length of string (“1111”) = 4
- Length of string (“010101”) = 6
- Length of string (“11110000”) = 8
- Length of string (“1111100000”) = 10
The maximum length of any string in the given language is 10. So, pumping length p will be 10+1 = 11
Step 02: if p = 11, no candidate string is found, as no candidate string exists; hence, nothing violates the pumping conditions. Hence, L satisfies the pumping lemma.
Case 02 Examples: Pumping Lemma For Infinite Regular Languages
If a language L is infinite and regular, then it satisfies the Pumping Lemma. Let explain some examples
Example 01: L = a(a+b)*
Step 1: Assume that the language L is regular. Assume p = 2
Step 2: Given a language, generate all possible strings starting with “a” over alphabets “a” and “b”.
L = {a, aa, ab, aaa, abb, aba, aab, aaaa,…………….}
Step 3: Choose a string, i.e., w = abb. The string we choose must be greater than or equal to the “p” values.
Step 4: Let split the given string into “xyz” where|xy| ≤ p and|y| ≥ 1
Let
- x = a
- y = bb
- z = epsilon
Not, Split “xyz” can be done in various ways by using the given conditions
Step 5: Now, check whether y = ab can pump using the condition(x yⁱ z ∈ L for all i ≥ 0) or not?
orignal string w = abb ∈ L
when i = 0, w = a ∈ L
when i = 1, w = abb ∈ L
When i = 2, w = abbbb ∈ L
When i = 3, w = abbbbbb ∈ L
so on,…
Step 6: If the value of “y” is at the 2nd position of the string w, then all pumping strings belong to the given language. General proof is also satisfied.
Step 7: Since all the pumping conditions are satisfied, no conclusion can be drawn about whether L is regular or not.
Important points of Example 1:
|
Example 02: L = (a+b)*a
Step 1: Assume that the language L is regular. Assume p = 2
Step 2: Given a language, generate all possible strings ending with “a” over alphabets “a” and “b”.
L = {a, aa, ba, aaa, bba, aba, bba, aaaa,…………….}
Step 3: Choose a string, i.e., w = bba. The string we choose must be greater than or equal to the “p” values.
Step 4: Let split the given string into “xyz” where|xy| ≤ p and|y| ≥ 1
Let
- x =b
- y = b
- z = a
Not, Split “xyz” can be done in various ways by using the given conditions
Step 5: Now, check whether y = ab can pump using the condition(x yⁱ z ∈ L for all i ≥ 0) or not?
orignal string w = bba∈ L
when i = 0, w = ba∈ L
when i = 1, w = bba ∈ L
When i = 2, w = bbba∈ L
When i = 3, w = bbbba ∈ L
so on,…
Step 6: If the value of “y” is at the first position of the string w, then all pumping strings belong to the given language. General proof is also satisfied.
Step 7: Since all the pumping conditions are satisfied, no conclusion can be drawn about whether L is regular or not.
Important points of Example 2:
|
Example 03: L = aaab*
Step 1: Assume that the language L is regular. Assume p = 4
Step 2: Given a language, generate all possible strings starting with “aaa” and ending with zero or more “b’s”.
L = {aaa, aaab, aaabb, aaabbb, aaabbb, aaabbbb,…………….}
Step 3: Choose a string, i.e., w = aaabb. The string we choose must be greater than or equal to the “p” values.
Step 4: Let split the given string into “xyz” where|xy| ≤ p and|y| ≥ 1
Let
- x =aaa
- y = b
- z = b
Not, Split “xyz” can be done in various ways by using the given conditions
Step 5: Now, check whether y = ab can pump using the condition(x yⁱ z ∈ L for all i ≥ 0) or not?
orignal string w = aaabb∈ L
when i = 0, w = aaab∈ L
when i = 1, w = aaabb ∈ L
When i = 2, w = aaabbb∈ L
When i = 3, w = aaabbbb ∈ L
so on,…
Step 6: If the value of “y” is at the 4th position of the string w, then all pumping strings belong to the given language. General proof is also satisfied.
Step 7: Since all the pumping conditions are satisfied, no conclusion can be drawn about whether L is regular or not.
Important points of Example 3:
|
Example 04: L = c(ab)*
Step 1: Assume that the language L is regular. Assume p = 3
Step 2: Given a language, generate all possible strings starting with “c” and ending with zero or more set of “ab”.
L = {c, cab, cabab, cababab, cabababab, cababababab,…………….}
Step 3: Choose a string, i.e., w = cabababab. The string we choose must be greater than or equal to the “p” values.
Step 4: Let split the given string into “xyz” where|xy| ≤ p and|y| ≥ 1
Let
- x =c
- y = ab
- z = ababab
Not, Split “xyz” can be done in various ways by using the given conditions
Step 5: Now, check whether y = ab can pump using the condition(x yⁱ z ∈ L for all i ≥ 0) or not?
orignal string w = cabababab∈ L
when i = 0, w = cababab∈ L
when i = 1, w = cabababab∈ L
When i = 2, w = cababababab∈ L
When i = 3, w = cabababababab∈ L
so on,…
Step 6: If the value of “y” is at the 2nd and 3rd position of the string w, then all pumping strings belong to the given language. General proof is also satisfied.
Step 7: Since all the pumping conditions are satisfied, no conclusion can be drawn about whether L is regular or not.
Important points of Example 4:
|
Example 05: L={an ∣ n≥0}
Step 1: Assume that the language L is regular. Assume p = 1
Step 2: It generates all strings consisting of only the symbol a, including the empty string.
L = { ε, a, aa, aaa, aaaa, … }
Step 3: Choose a string, i.e., w = aaa. The string we choose must be greater than or equal to the “p” values.
Step 4: Let split the given string into “xyz” where|xy| ≤ p and|y| ≥ 1
Let
- x =epsilon
- y = a
- z = aa
Not, Split “xyz” can be done in various ways by using the given conditions
Step 5: Now, check whether y = ab can pump using the condition(x yⁱ z ∈ L for all i ≥ 0) or not?
orignal string w = aaa∈ L
when i = 0, w = aa∈ L
when i = 1, w = aaa∈ L
When i = 2, w = aaaa∈ L
When i = 3, w = aaaaa∈ L
so on,…
Step 6: If the value of “y” is at the first position of the string w, then all pumping strings belong to the given language. General proof is also satisfied.
Step 7: Since all the pumping conditions are satisfied, no conclusion can be drawn about whether L is regular or not.
Important points of Example 5:
|
Example 06: L={a3 , a5 , a7 , ……………} or L={a2n+1 ∣ n≥1}
Step 1: Assume that the language L is regular. Assume p = 4
Step 2: This language contains strings of a with odd length starting from 3.
L = { aaa, aaaaa, aaaaaaa, aaaaaaaaa, aaaaaaaaaaa, … }
Step 3: Choose a string, i.e., w = aaaaa. The string we choose must be greater than or equal to the “p” values.
Step 4: Let split the given string into “xyz” where|xy| ≤ p and|y| ≥ 1
Let
- x =aa
- y = aa
- z = a
Not, Split “xyz” can be done in various ways by using the given conditions
Step 5: Now, check whether y = ab can pump using the condition(x yⁱ z ∈ L for all i ≥ 0) or not?
orignal string w = aaaaa∈ L
when i = 0, w = aaa∈ L
when i = 1, w = aaaaa∈ L
When i = 2, w = aaaaaaa∈ L
When i = 3, w = aaaaaaaaa∈ L
so on,…
Step 6: If the value of “y” is at the 4th and 5th position of the string w, then all pumping strings belong to the given language. General proof is also satisfied.
Step 7: Since all the pumping conditions are satisfied, no conclusion can be drawn about whether L is regular or not.
Important points of Example 6:
|
Example 07: L=(011)*
Step 1: Assume that the language L is regular. Assume p = 3
Step 2: L=(011)∗ means zero or more repetitions of “011”
- L = {ϵ, 011, 011011, 011011011, 011011011011, … }
Step 3: Choose a string, i.e., w = 011011. The string we choose must be greater than or equal to the “p” values.
Step 4: Let split the given string into “xyz” where|xy| ≤ p and|y| ≥ 1
Let
- x = ϵ
- y = 011
- z =011
Not, Split “xyz” can be done in various ways by using the given conditions
Step 5: Now, check whether y = ab can pump using the condition(x yⁱ z ∈ L for all i ≥ 0) or not?
orignal string w = 011011∈ L
when i = 0, w = 011∈ L
when i = 1, w = 011011∈ L
When i = 2, w = 011011011∈ L
When i = 3, w = 011011011011∈ L
so on,…
Step 6: If the value of “y” is at the first three positions of the string w, then all pumping strings belong to the given language. General proof is also satisfied.
Step 7: Since all the pumping conditions are satisfied, no conclusion can be drawn about whether L is regular or not.
Important points of Example 7:
|
Example 08: L=0(01)*1
Step 1: Assume that the language L is regular. Assume p = 3
Step 2: L = 0(01)∗1 means:
-
String starts with 0
-
Followed by zero or more repetitions of “01”
-
Ends with 1
- Example: L = {01, 0011, 001011, 00101011, …}
Step 3: Choose a string, i.e., w = 0011. The string we choose must be greater than or equal to the “p” values.
Step 4: Let split the given string into “xyz” where|xy| ≤ p and|y| ≥ 1
Let
- x = 0
- y = 01
- z =1
Not, Split “xyz” can be done in various ways by using the given conditions
Step 5: Now, check whether y = ab can pump using the condition(x yⁱ z ∈ L for all i ≥ 0) or not?
orignal string w = 0011∈ L
when i = 0, w = 01∈ L
when i = 1, w = 0011∈ L
When i = 2, w = 001011∈ L
When i = 3, w = 00101011∈ L
so on,…
Step 6: If the value of “y” is at the first three positions of the string w, then all pumping strings belong to the given language. General proof is also satisfied.
Step 7: Since all the pumping conditions are satisfied, no conclusion can be drawn about whether L is regular or not.
Important points of Example 8:
|
Example 09: L=0(01)*1
Step 1: Assume that the language L is regular. Assume p = 3
Step 2: L = 0(01)∗1 means:
-
String starts with 0
-
Followed by zero or more repetitions of “01”
-
Ends with 1
- Example: L = {01, 0011, 001011, 00101011, …}
Step 3: Choose a string, i.e., w = 0011. The string we choose must be greater than or equal to the “p” values.
Step 4: Let split the given string into “xyz” where|xy| ≤ p and|y| ≥ 1
Let
- x = 0
- y = 01
- z =1
Not, Split “xyz” can be done in various ways by using the given conditions
Step 5: Now, check whether y = ab can pump using the condition(x yⁱ z ∈ L for all i ≥ 0) or not?
orignal string w = 0011∈ L
when i = 0, w = 01∈ L
when i = 1, w = 0011∈ L
When i = 2, w = 001011∈ L
When i = 3, w = 00101011∈ L
so on,…
Step 6: If the value of “y” is at the first three positions of the string w, then all pumping strings belong to the given language. General proof is also satisfied.
Step 7: Since all the pumping conditions are satisfied, no conclusion can be drawn about whether L is regular or not.
Important points of Example 9:
|
Example 10: L=0(01)*1
Step 1: Assume that the language L is regular. Assume p = 4
Step 2: L = 00(01)∗1 means:
-
String starts with 00
-
Followed by zero or more repetitions of “01”
-
Ends with 1
- Example: L = {001, 00011, 0001011, 000101011, …}
Step 3: Choose a string, i.e., w = 00011. The string we choose must be greater than or equal to the “p” values.
Step 4: Let split the given string into “xyz” where|xy| ≤ p and|y| ≥ 1
Let
- x = 00
- y = 01
- z =1
Not, Split “xyz” can be done in various ways by using the given conditions
Step 5: Now, check whether y = ab can pump using the condition(x yⁱ z ∈ L for all i ≥ 0) or not?
orignal string w = 00011∈ L
when i = 0, w = 001∈ L
when i = 1, w = 00011∈ L
When i = 2, w = 0001011∈ L
When i = 3, w = 000101011∈ L
so on,…
Step 6: If the value of “y” is at the first three positions of the string w, then all pumping strings belong to the given language. General proof is also satisfied.
Step 7: Since all the pumping conditions are satisfied, no conclusion can be drawn about whether L is regular or not.
Important points of Example 10:
|
Case 03 Examples: Pumping Lemma For Infinite Non-Regular Languages
If a language L is infinite and non-regular, then it does not satisfy (fails) the Pumping Lemma for regular languages.
Example 01: L={anbn ∣ n≥0}
Step 1: Assume that the language L is regular. Assume p = 4
Step 2: This language contains strings with equal number of a’s followed by b’s.
L = { ε, ab, aabb, aaabbb, aaaabbbb, …}
Step 3: Choose a string, i.e., w = aaabbb. The string we choose must be greater than or equal to the “p” values.
Step 4: Let split the given string into “xyz” where|xy| ≤ p and|y| ≥ 1
Let
- x =aa
- y = ab
- z = bb
Not, Split “xyz” can be done in various ways by using the given conditions
Step 5: Now, check whether y = ab can pump using the condition(x yⁱ z ∈ L for all i ≥ 0) or not?
orignal string w = aaabbb∈ L
when i = 0, w = aabb∈ L
when i = 1, w = aaabbb ∈ L
When i = 2, w = aaababbb ∉ L
When i = 3, w = aaabababbb ∉L
so on,…
Step 6: By applying general proof, we cannot get any suitable place of “y” in “w” where all strings should pump.
Step 7: Since not all the pumping conditions are satisfied. So, L is not regular.
Example 02: L= {w ∣ #a(w) = #b(w) }
Step 1: Assume that the language L is regular. Assume p = 3
Step 2: All strings w that contain an equal number of a and b symbols, in any order
L = {ε, ab, ba, aabb, abab, bbaa,aaabbb …}
Step 3: Choose a string, i.e., w = aaabbb. The string we choose must be greater than or equal to the “p” values.
Step 4: Let split the given string into “xyz” where|xy| ≤ p and|y| ≥ 1
Let
- x =aa
- y = a
- z = bbb
Not, Split “xyz” can be done in various ways by using the given conditions
Step 5: Now, check whether y = ab can pump using the condition(x yⁱ z ∈ L for all i ≥ 0) or not?
orignal string w = aaabbb∈ L
when i = 0, w = aabbb ∉ L
when i = 1, w = aaabbb ∈ L
When i = 2, w = aaaabbb ∉ L
When i = 3, w = aaaaabbb ∉L
so on,…
Very important: Suppose if we increase “p” range to “10”, then a possible string like “aaaaaaaaaaabbbbbbbbbbb” will also violate.
Step 6: By applying general proof, we cannot get any suitable place of “y” in “w” where all strings should pump.
Step 7: Since not all the pumping conditions are satisfied. So, L is not regular.
Note: L= {w ∣ #a(w) = #b(w) } in not equal to (ab)* becuase (ab)* cannot genrate strings like abba,….
Example 03: L= L={a2ibi ∣ i≥0}
Step 1: Assume that the language L is regular. Assume p = 6
Step 2: This represents strings with twice as many a’s as b’s, where all a’s come before b’s.
L = {ε, aab, aaaabb, aaaaaabbb, …}
Step 3: Choose a string, i.e., w = aaaabb. The string we choose must be greater than or equal to the “p” values.
Step 4: Let split the given string into “xyz” where|xy| ≤ p and|y| ≥ 1
Let
- x =aaa
- y = ab
- z = b
Not, Split “xyz” can be done in various ways by using the given conditions
Step 5: Now, check whether y = ab can pump using the condition(x yⁱ z ∈ L for all i ≥ 0) or not?
orignal string w = aaaabb∈ L
when i = 0, w = aaab ∉ L
when i = 1, w = aaaabb∈ L
When i = 2, w = aaaababb ∉ L
When i = 3, w = aaaabababb ∉L
so on,…
Step 6: By applying general proof, we cannot get any suitable place of “y” in “w” where all strings should pump.
Step 7: Since not all the pumping conditions are satisfied. So, L is not regular.
Note: whatever “y” you take and when you repeat it 0 times, then a2ibi will never meet.
Prove Language is not Regular Using Pumping Lemma (Contradiction)To prove that a language is not Regular using Pumping Lemma , follow the below steps: (We prove using Contradiction)
|
Pumping Lemma – Shortcut Method May Help You
Example 01: Using the Pumping Lemma, prove that the language A = { yy | y ∈ {0,1}* } is not Regular
Below is a descriptive diagram that explains why the language A = { yy | y ∈ {0,1}* } is not regular.

A straightforward, short description of the given example to prove that the language A = { yy | y ∈ {0,1}* } is not Regular is given below, by using different “p” and “i” values
- We want to prove A = {yy | y ∈ {0,1}*} is not regular.
- Assume it is regular and choose a string S = 0101 from A.
- Let pumping length be p = 2, so |xy| ≤ 2 and |y| > 0.
- Split: x = 0, y = 1, z = 01 → S = xyz = 0101.
- Pump y: xy²z = 01101, which is not in the form yy.
- So, pumping fails → A is not regular.
Example 02: Using Pumping Lemma prove that the language A = { anbn | n ≥ 0 } is not Regular
Below is a descriptive diagram that explains why the language A = { anbn | n ≥ 0 } is not regular.

A straightforward, short description of the given example to prove that the language A = { anbn | n ≥ 0 } is not Regular is given below, by using different “p” and “i” values
- We want to prove that A = { aⁿbⁿ | n ≥ 0 } is not regular.
- Assume A is regular and let the pumping length be p = 3.
- Choose a string S = aaabbb from A (n = 3).
- Split S into x = aa, y = a, z = bbb, where |xy| ≤ p and |y| > 0.
- Pump y: xy²z = aaaabbb, which has 4 a’s and 3 b’s → not in A.
- So, the string after pumping is not in the language → A is not regular
Example 03: Using Pumping Lemma prove that the language A = { anb2n | n ≥ 0 } is not Regular
Below is a descriptive diagram that explains why the language A = { anb2n | n ≥ 0 } is not regular.

A simple, short description of the given example to prove that the language A = { anb2n | n ≥ 0 } is not Regular is given below, by using different “p” and “i” values
- We want to prove that A = { aⁿb²ⁿ | n ≥ 0 } is not regular.
- Assume A is regular and let the pumping length be p = 3.
- Choose a string S = aaabbbbbb from A (n = 3 → 3 a’s and 6 b’s).
- Split S into x = aa, y = a, z = bbbbbb, where |xy| ≤ p and |y| > 0.
- Pump y: xy²z = aaaabbbbbb, which has 4 a’s and 6 b’s → not in A (should be a⁴b⁸).
- So, the string after pumping is not in the language → A is not regular













