Epsilon NFA (∈-NFA)
Epsilon NFA (∈-NFA) is similar to the NFA but with a little difference in that, it has an epsilon (∈) transition that NFA doesn’t have. A Transition that does not consume any input symbol is called an ε-transitions. Epsilon NFA (∈-NFA) is also called a null NFA or an NFA lambda.
- ∈-NFA state diagrams usually label Epsilon with the Greek letter “∈”. It is also called lambda.
- ∈-transitions give a convenient way of designing the machine systems.
- Due to ε-transitions, the first string of language may be empty.
Note: ∈ab∈a = aba, where ∈ is empty. Epsilon (∈) transition is also known as an empty move or empty transition.
Formal Definition of Epsilon-NFA
The formal definition of ∈-NFA is represented through 5-tuple (Q, ∑, δ, q0, F) where,
- Q is a finite set of all states (q0, q1, q2, …, qn) where n is a finite number.
- ∑ Is a finite set of symbols called the alphabet. i.e. {0, 1}.
- δ : Q x (∑ U ∈) → 2Q is a total function called as transition function.
- q0 is the initial state from which any input is processed (q0 ∈ Q).
- F is a set of final states, where F will be a subset ( ⊆ ) of Q.
|
Important !!
|
Examples of Epsilon-NFA
There are various examples of epsilon-NFA. Let’s explain some of them.
∈ – NFA: Example 01
Draw an epsilon NFA that accepts the string “ab”.
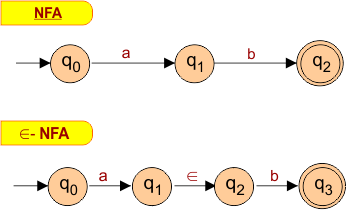
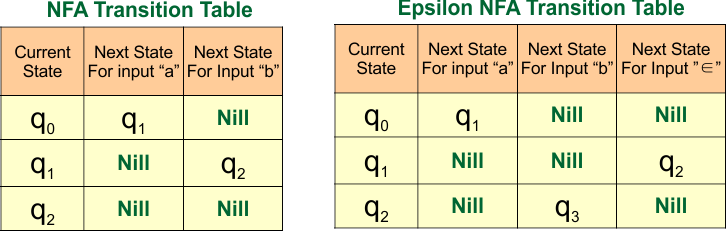
The transition table for the above NFA and epsilon NFA diagram is given below
∈ – NFA: Example 02
Draw an epsilon NFA that accepts the string “a or b”.
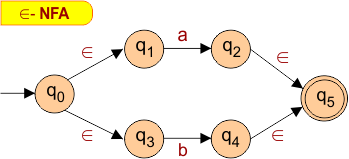
The transition table for the above epsilon NFA diagram is given below
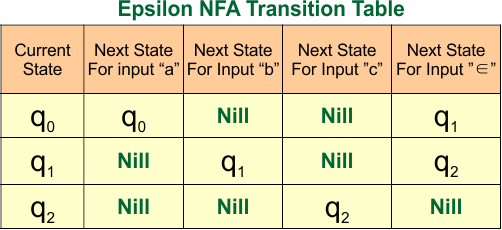
∈ – NFA: Example 03
Draw an epsilon NFA that accepts the string “a, b, or c”. 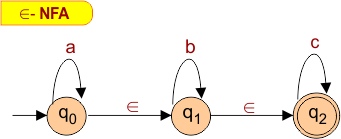
The transition table for the above epsilon NFA diagram is given below
Epsilon-NFA: Example 04
Draw an epsilon NFA that accepts the string “a*”.
The transition table for the above epsilon NFA diagram is given below
∈ – NFA: Example 05
Create a ∈-NFA for regular expression: ((b)*a)*
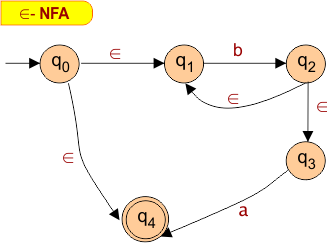
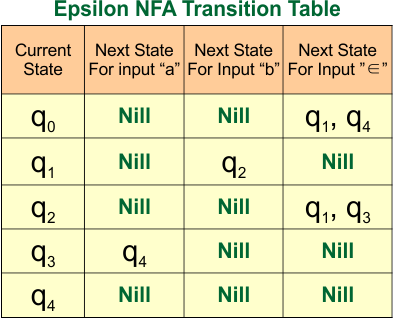
The transition table for the above epsilon NFA diagram is given below
Epsilon Closure in Epsilon NFA
For each state in the Epsilon-NFA, determine its epsilon closure. This involves identifying all the states that can be reached only through epsilon transitions, including the state itself. Understanding the epsilon closure is essential for tracking which states can be accessed without processing any input symbols.
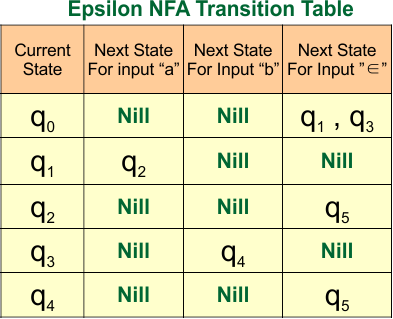
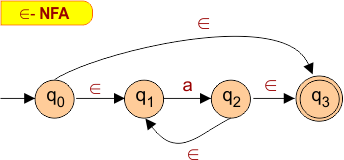
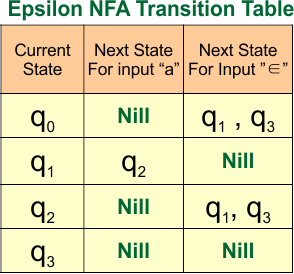
For Example, consider the following epsilon NFA

In the above epsilon NFA, the epsilon closure of all states is given below
- The epsilon closure of state “q0” is q0, q2, q1, and q3.
- The epsilon closure of state “q1” is q1 and q3.
- The epsilon closure of state “q2” is only q2 (itself).
- The epsilon closure of state “q3” is only q3 (itself).
Epsilon closure helps in converting epsilon NFA to NFA and epsilon NFA to DFA.
Epsilon NFA To NFA Conversion Algorithm
Now we will see some examples of epsilon NFA to NFA conversion using the following algorithm
Epsilon NFA To NFA Conversion Algorithm
If the epsilon exists between any two states in an automata, then the removal of epsilon through some rules is called the elimination of epsilon from the epsilon-NFA.
Suppose there are two vertices / states, V1 and V2; the epsilon between them is below.
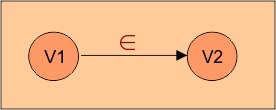
Look at the following steps for the elimination of epsilon from epsilon NFA
- Step 1: First, find the epsilon location. Label the vertices as V1 (start of epsilon edge) and V2 (end of edge) where epsilon exists.
- Step 2: Find all edges starting from V2. Simply, duplicate V2 edges to V1 with the same labels. Now, remove the epsilon
- Step 3: If V1 is the initial state, make V2 initial. If V2 is the final state, make V1 final. Remove all unreachable states (if they exist).
- Step 4: Check if there are any more epsilons. Repeat steps 1 to 3 until no epsilons remain.
Note: if more than one epsilon exists in the epsilon-NFA, then first remove the epsilon that is far away from the initial state.
Tip: An unreachable state cannot be reached from the initial state against any input.
Let’s discuss various examples according to the given steps for epsilon NFA to NFA conversions
Example 01: Convert Epsilon NFA to NFA
Consider the following epsilon NFA
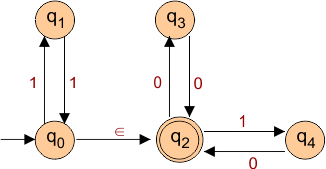
Step 01: Find Epsilon Location
Epsilon exists between q0 and q2. So, q0 becomes V1 and q2 becomes V2. Now apply the steps of epsilon removal.
Step 02: Find starting edges from V2, duplicate it to V1, Remove Epsilon
Two edges are starting from V2 (q2)
- First Edge: Goes to q3 for input “0”.
- Second Edge: Goes to q4 for input “1”.
Simply, duplicate these edges (starting from V2) to V1 and remove the epsilon edge.

Step 03: Check Initial, Final, and Unreachable State Conditions
- Initial state condition: As V1 (q0) is the initial state. So V2(q2) becomes initial as well.
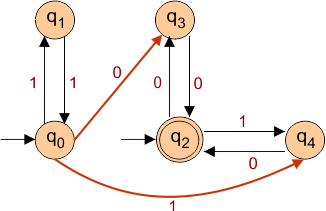
- Final state condition: As V2 (q2) is a final state. So V1(q0) also becomes the final state.
- Unreachable state condition: There is no unreachable state. So we cannot remove any state from the above NFA
Step 04: Check for any more Epsilon
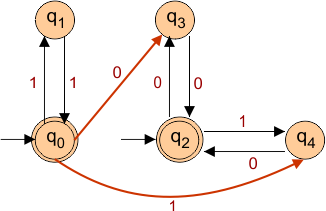
Only the single epsilon was given in the example, which had already been removed. So, the final NFA is given below

Example 02: Convert Epsilon NFA to NFA
Consider the following epsilon NFA

Step 01: Find Epsilon Location
In the above epsilon NFA, there are two epsilons.
- First, Epsilon exists between q0 and q1.
- Second Epsioln exists between q1 and q4.
First, we remove the second epsilon, because it is far away from the initial state.
Step 02: Find starting edges from V2, duplicate it to V1, Remove Epsilon
Only single edges start from V2 (q4) and go to q5 for input “0”. Simply duplicate this edge V1 (q0) and remove the epsilon edge with its label. we get the following

Step 03: Check Initial, Final, and Unreachable State Conditions
- Initial state condition: As V1 (q1) is not an initial state. So V2(q4) cannot be an initial state; NFA remains unchanged.
- Final state condition: As V2 (q4) is not a final state. So V1(q1) cannot be a final state. NFA remains unchanged.
- Unreachable state condition: A constructed NFA has one unreachable state, which is q4. Simply remove this state along with its outgoing edges.

Step 04: Check for any more Epsilon
Yes, still there exists one more epsilon edge between “q0” and “q1”. So, repeat the first 3 steps to remove the remaining epsilons.
Again, step 1: Find Epsilon Location
Epsilon exists between q0 and q1. So, q0 becomes V1 and q1 becomes V2. Now apply the steps of epsilon removal.
Again, step 02: Find starting edges from V2, duplicate it to V1, and Remove Epsilon
Only single edges start from V2 (q1) and go to q3 for input “0”. Simply, duplicate this edge with its label to V1 (q0) and remove the epsilon edge.

Again, Step 03: Check Initial, Final, and Unreachable State Conditions
- Initial state condition: As V1 (q0) is an initial state. So V2(q1) becomes initial as well. As given below
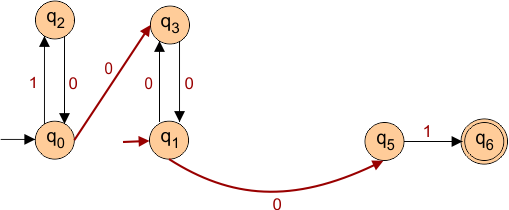
- Final state condition: As V2 (q1) is not a final state. So V1(q0) cannot be a final. NFA remains unchanged
- Unreachable state condition: There is no unreachable state. So we cannot remove any state from the above NFA
Again, step 04: Check for any more Epsilon
As there were two epsilons given initially in the example, both are removed. No more epsilon exists.
Final Result:
So the final NFA, after removing all epsilons from the given epsilon NFA, is given below
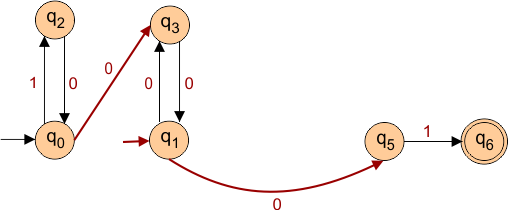
Example 03: Convert Epsilon NFA to NFA
Consider the following epsilon NFA
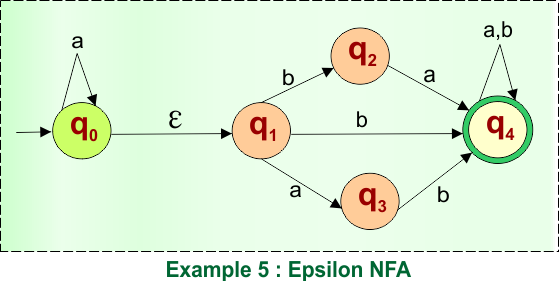
Step 01: Find Epsilon Location
Epsilon exists between q0 and q1. So, q0 becomes V1 and q1 becomes V2. Now apply the steps of epsilon removal.
Step 02: Find starting edges from V2, duplicate it to V1, Remove Epsilon
Three edges are starting from V2 (q1)
- First Edge: Goes to q2 for input “b”.
- Second Edge: Goes to q4 for input “b”.
- Third Edge: Goes to q3 for input “a”.
Simply, duplicate these edges (starting from V2) to V1 and remove the epsilon edge.
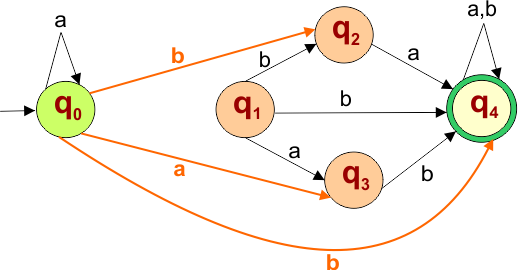
Step 03: Check Initial, Final, and Unreachable State Conditions
- Initial state condition: As V1 (q0) is the initial state. So V2(q1) becomes initial as well.

- Final state condition: As V2 (q1) is not the final state. So V1(q0) can not be the final state.
- Unreachable state condition: There is no unreachable state because “q1” is now the starting state as well. So we cannot remove any state from the above NFA
Step 04: Check for any more Epsilon
Only the single epsilon was given in the example, which had already been removed. So, the final NFA is given below
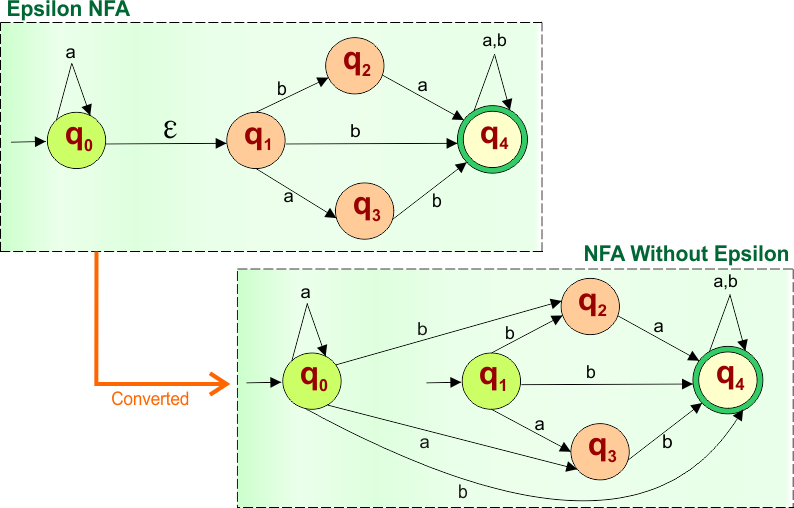
Comparison of ε-NFA, NFA, and DFA
ε-NFA, NFA, and DFA are models of finite automata used to recognize regular languages, differing in how they handle transitions. A detailed comparison summary is given below
| Feature | DFA | NFA | ε-NFA |
|---|---|---|---|
| 1. Determinism | Fully Deterministic | Nondeterministic | Highly Nondeterministic (due to ε-moves) |
| 2. Epsilon (ε) Transitions | Not allowed | Not allowed | Allowed (transition without input) |
| 3. Transition Function | δ: Q × Σ → Q | δ: Q × Σ → 2^Q | δ: Q × (Σ ∪ {ε}) → 2^Q |
| 4. Number of Transitions per Input | Only one possible next state | Multiple possible next states | Multiple or ε-moves to new states |
| 5. Ease of Construction | Complex for large patterns | Easier than DFA | Simplest to design (modular, flexible) |
| 6. Execution Paths | Single unique path per input string | May have multiple paths | May explore paths using ε before input |
| 7. Acceptance Criteria | Accepts if the final state is reached | Accepts if any path leads to the final state | Same as NFA with ε-transitions |
| 8. Language Recognition Power | Regular languages only | Regular languages only | Regular languages only |
| 9. Conversion Possibility | Already deterministic | Can be converted to DFA | Can be converted to NFA/DFA via ε-closure |
| 10. Practical Use Cases | Lexical analyzers, compilers | Intermediate models in automata design | Used for regex engines, modular NFA design |
Applications of ε-NFA
Here are simplified applications of ε-NFA
- Regex to Automata Conversion – ε-NFA helps in converting regular expressions to automata easily using ε-transitions.
- Modular Automaton Design – Breaks complex problems into smaller NFAs and connects them using ε-transitions.
- Compiler Design – Used in building lexical analyzers during the token generation phase.
- Parallel Path Execution – Allows exploring multiple paths without consuming input, useful in theoretical modeling.
- Simplifying NFA Construction – Makes it easier to construct NFAs with fewer transitions for complex patterns.













