CFL in TOC
Context-free grammar has production rules that are used to generate cfl (context-free language) in toc. Context-free languages are accepted by push-down automata (PDA).
- PDA accepts all Regular languages and CFL.
- For all context-free languages, there must be one comparison in terminals of string e L= {anbn n>=0}
A context-free Grammar (CFG) is a 4-tuple such that
G = (V , T , P , S)
where
- V = Finite set of variables / non-terminal symbols. These are denoted by capital letters.
- T = Finite set of terminal symbols. These are used to replace the variables. These are denoted by lowercase letters.
- P = Production rules are used to generate a CFL. i.e. A → α , where A ∈ V and α ∈ (V ∪ T)*. Remember that the left side must contain only one variable, but the right side ((V ∪ T)*) may contain more than one terminal and non-terminal.
- S = Start symbol
Examples Of CFL in TOC
In this lecture, we will provide various examples of context-free languages (CFLs) along with their corresponding grammar. Each CFL example will discuss the CFL, its CFG, and include a descriptive diagram of the CFG derivation string.
Almost 12 examples of CFL in TOC are discussed in this lecture. Let’s start one by one.
CFL Example 1: L = {anbn ∣ n≥0}
The language L = {anbn ∣ n≥0} will generate the strings where the number of “a’s” is equal to the number of “b’s”. For “n = 0,” there are no values (ε) for “a” and “b.”
Output strings for various values of n:
- For “n = 0”, output string = ε
- For “n = 1”, output string = ab
- For “n = 2”, output string = aabb
- For “n = 3”, output string = aaabbb
- For “n = 4”, output string = aaaabbbb
- So on..
CFG for L = {anbn ∣ n≥0}
Let’s define the CFG for L = {anbn ∣ n≥0} through its 4 tuples G = (V, Σ, R, S)
-
Variables (V): {S}
-
Alphabet (Σ): {a, b}
-
Rules (R):
S → aSb | ε
-
Start Symbol: S
The following diagram shows the CFG and the string “aabb” derivation from L = {anbn ∣ n≥0}
CFL Example 2: L = {anbn ∣ n≥1}
Give language L = {anbn ∣ n≥1} will generate the strings where the number of “a’s” is equal to the number of “b’s”. As the value of “n” starts from “1” instead of “0”, so empty string (ε) is not allowed.
Output strings for various values of n:
- For “n = 1”, output string = ab
- For “n = 2”, output string = aabb
- For “n = 3”, output string = aaabbb
- For “n = 4”, output string = aaaabbbb
- So on..
CFG for L = {anbn ∣ n≥1}
Let’s define the CFG for L = {anbn ∣ n≥1} through its 4 tuples G = (V, Σ, R, S)
-
Variables (V): {S}
-
Alphabet (Σ): {a, b}
-
Rules (R):
S → aSb | ab -
Start Symbol: S
The following diagram shows the CFG and the string “aaabbb” derivation from L = {anbn ∣ n≥1}

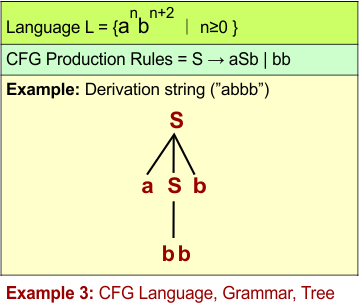
CFL Example 3: L = {anbn+2 ∣ n≥0}
The given language L = {anbn+2 ∣ n≥0} will generate strings where the number of “b”s is exactly two more than the number of “a”s.
Output strings for various values of n:
- For n = 0, output string =
bb - For n = 1, output string =
abb - For n = 2, output string =
aabbbb - For n = 3, output string =
aaabbbbb - For n = 4, output string =
aaaabbbbbb - So on…
CFG for L = {anbn+2 ∣ n≥0}
Let’s define the CFG for L = {anbn+2 ∣ n≥0} through its 4 tuples G = (V, Σ, R, S)
-
Variables (V): {S}
-
Alphabet (Σ): {a, b}
-
Rules (R):
S → aSb | bb
-
Start Symbol: S
Note: The rule S → aSb ensures equal number of as and bs. The rule S → bb ensures two extra bs in the end of string.
The following diagram shows the CFG and the string “abbb” derivation from L = {anbn+2 ∣ n≥0}
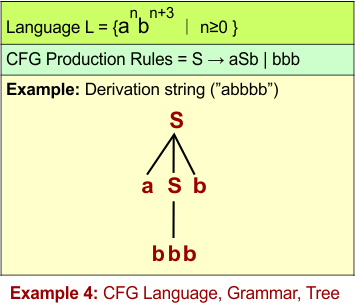
CFL Example 4: L = {anbn+3 ∣ n≥0 }
The given language L = {anbn+3 ∣ n≥0 } will generate strings where the number of “b”s is exactly three more than the number of “a”s.
Output strings for various values of n:
- For n = 0, output string =
bbb - For n = 1, output string =
abbbb - For n = 2, output string =
aabbbbb - For n = 3, output string =
aaabbbbbb - For n = 4, output string =
aaaabbbbbbb - So on…
CFG for L = { anbn+3 ∣ n ≥ 0 }
Let’s define the CFG for L = { anbn+3 ∣ n ≥ 0 } through its 4 tuples G = (V, Σ, R, S)
-
Variables (V): {S}
-
Alphabet (Σ): {a, b}
-
Rules (R):
S → aSb | bbb
-
Start Symbol: S
Note: The rule S → aSb ensures equal numbers of as and bs are matched. The rule S → bbb adds three extra bs
The following diagram shows the CFG and the string “abbbb” derivation from L = {anbn+3 ∣ n≥0 }
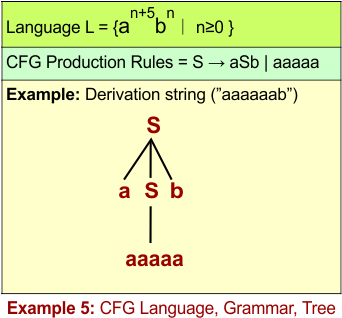
CFL Example 5: L = {an+5bn ∣ n≥0 }
The given language L = {an+5bn ∣ n≥0 } will generate strings where the number of “a” is exactly five more than the number of “a”.
Output strings for various values of n:
- For n = 0, output string =
aaaaa - For n = 1, output string =
aaaaaab - For n = 2, output string =
aaaaaaabb - For n = 3, output string =
aaaaaaaabbb - For n = 4, output string =
aaaaaaaaabbbb - So on…
CFG for L = { an+5bn ∣n ≥ 0 }
Let’s define the CFG for L = { an+5bn ∣n ≥ 0 } through its 4 tuples G = (V, Σ, R, S)
-
Variables (V): {S}
-
Alphabet (Σ): {a, b}
-
Rules (R):
S → aSb |aaaaa -
Start Symbol: S
Note: The rule S → aSb ensures equal numbers of as and bs are matched. The rule S → aaaaa adds five extra a’s.
The following diagram shows the CFG and the string “aaaaaab” derivation from L = {an+5bn ∣ n≥0 }
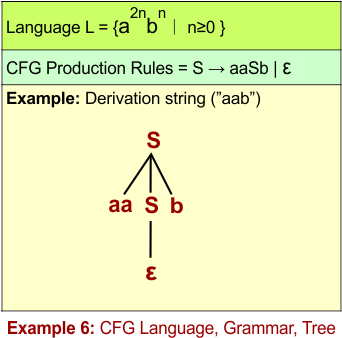
CFL Example 6: L = {a2nbn ∣ n≥0 }
The given language L = {a2nbn ∣ n≥0 } will generate strings where the number of “a”s is exactly twice the number of “b”s.
Output strings for various values of n:
- For n = 0, output string = ε (empty string)
- For n = 1, output string =
aab - For n = 2, output string =
aaaabb - For n = 3, output string =
aaaaaabbb - For n = 3, output string =
aaaaaaaabbbb - So on…
CFG for L = { a2nbn ∣ n ≥ 0 }
Let’s define the CFG for L = {a2nbn ∣ n ≥ 0 } through its 4 tuples G = (V, Σ, R, S)
-
Variables (V): {S}
-
Alphabet (Σ): {a, b}
-
Rules (R):
S → aaSb | ε -
Start Symbol: S
Note: The rule S → aaSb generates two a’s and one b per recursive step. The rule S → ε allows the process to stop, handling the base case n=0.
The following diagram shows the CFG and the string “aab” derivation from L = {a2nbn ∣ n≥0 }
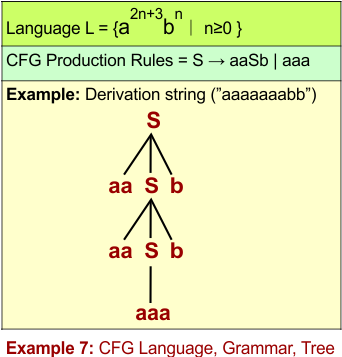
CFL Example 7: L = {a2n+3 bn ∣ n≥0 }
The given language L = {a2n+3bn ∣ n≥0 } will generate Output strings for various values of n:
| n | a’s count | b’s count | String |
|---|---|---|---|
| 0 | 3 | 0 | aaa |
| 1 | 5 | 1 | aaaaab |
| 2 | 7 | 2 | aaaaaaabb |
| 3 | 9 | 3 | aaaaaaaaabbb |
| 4 | 11 | 4 | aaaaaaaaaaabbbb |
| … | … | … | … |
CFG for L = { a2n+3bn ∣ n ≥ 0 }
Let’s define the CFG for L = { a2n+3bn ∣ n ≥ 0 } through its 4 tuples G = (V, Σ, R, S)
-
Variables (V): {S}
-
Alphabet (Σ): {a, b}
-
Rules (R):
S → aaSb | aaa -
Start Symbol: S
Note: The rule S → aaSb generates two a’s and one b per recursive step. The rule S → aaa adds five extra a’s.
The following diagram shows the CFG and the string “aaaaaaabb” derivation from L = {a2n+3bn ∣ n≥0 }
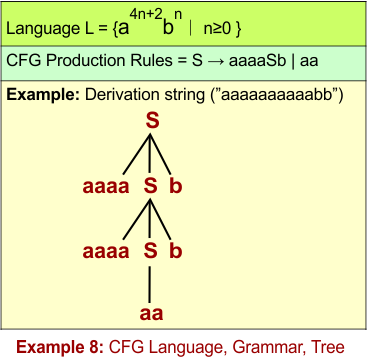
CFL Example 8: L = {a4n+2 bn ∣ n≥0 }
This language defines strings where:
-
The number of a’s is exactly 4n+2
-
The number of b’s is exactly n
Output strings for various values of n:
| n | a’s count | b’s count | String |
|---|---|---|---|
| 0 | 2 | 0 | aa |
| 1 | 6 | 1 | aaaaaab |
| 2 | 10 | 2 | aaaaaaaaaabb |
| 3 | 14 | 3 | aaaaaaaaaaaaaabbb |
| … | … | … | … |
CFG for L = { a4n+2bn ∣ n ≥ 0 }
Let’s define the CFG for L = { a4n+2bn ∣ n ≥ 0 } through its 4 tuples G = (V, Σ, R, S)
-
Variables (V): {S}
-
Alphabet (Σ): {a, b}
-
Rules (R):
S → aaaaSb | aa -
Start Symbol: S
The following diagram shows the CFG and the string “aaaaaaaaaabb” derivation from L = { a4n+2bn ∣ n ≥ 0 }
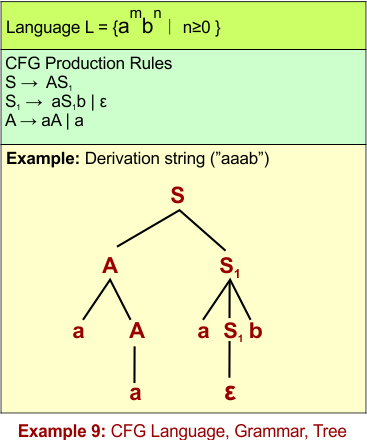
CFL Example 9: L = {ambn ∣ m>n, m≥0, n≥0}
This language consists of strings where:
-
Any number of a’s and b’s can appear
-
But the number of a’s must be strictly greater than the number of b’s
Examples of valid strings:
| m | n | String | Valid? |
|---|---|---|---|
| 1 | 0 | a |
yes |
| 2 | 0 | aa |
yes |
| 2 | 1 | aab |
yes |
| 3 | 2 | aaabb |
yes |
| 3 | 3 | aaabbb |
no (m = n) |
| 2 | 3 | aabbb |
no (m < n) |
CFG for L= {ambn ∣ m>n, m≥0, n≥0}`
Let’s define the CFG for L = {ambn ∣ m>n, m≥0, n≥0} through its 4-tuples G = (V, Σ, R, S)
-
Variables (V): {S, S1, A}
-
Alphabet (Σ): {a, b}
-
Rules (R):
S → AS1S1 → aS1b | ε // matches equal a's and b'sA → aA | a // adds at least one extra 'a' (ensures m > n)
-
Start Symbol: S
|
Following Rules used when L= {ambn ∣ m≥n, m≥0, n≥0}
S → AS1 S1 → aS1b | ε
A → aA | ε
|
The following diagram shows the CFG and the string “aaab” derivation from L = {ambn ∣ m>n, m≥0, n≥0}
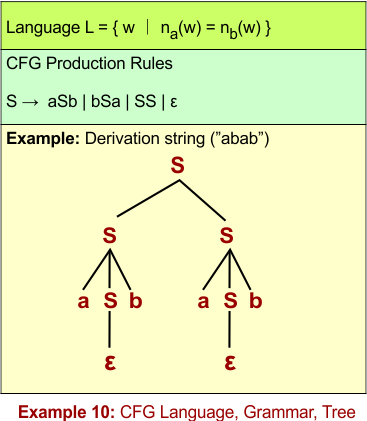
CFL Example 10: L = { w ∣ na(w) = nb(w) }
| Problem Explain: Find a string (W) in language (L) such that ( | ) the number of “a’s” in string {na(w)} is equal to the number of “b’s” in string {nb(w)} |
This language consists of strings where:
-
Any number of a’s and b’s in any order can appear.
-
But the number of a’s must be equal to the number of b’s
Examples of valid strings:
| String | na(w) | nb(w) | Valid? |
|---|---|---|---|
| ε | 0 | 0 | yes |
| ab | 1 | 1 | yes |
| ba | 1 | 1 | yes |
| aabb | 2 | 2 | yes |
| abab | 2 | 2 | yes |
| abb | 1 | 2 | no |
| aaabbb | 3 | 3 | yes |
| aabbb | 2 | 3 | no |
| abbaab | 3 | 3 | yes |
CFG for L = { w ∣ na(w) = nb(w) }
Let’s define the CFG for L = { w ∣ na(w) = nb(w) } through its 4 tuples G = (V, Σ, R, S)
-
Variables (V): {S}
-
Alphabet (Σ): {a, b}
-
Rules (R):
S → aSb | bSa | SS | ε -
Start Symbol: S
Tip: S → aSb | bSa | ε, cannot produce “abba” type of string. which is handled through S → aSb | bSa |SS| ε |
The following diagram shows the CFG and the string “abab” derivation from L = L = { w ∣ na(w) = nb(w) }
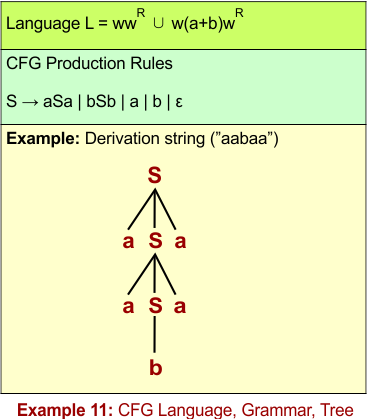
CFL Example 11: L = wwR ∪ w(a+b)wR
Problem Explain:
Together through union, these define all palindromes over the alphabet {a, b}. |
This language consists of the following strings of palindromes over {a, b}. The table is organized by string length:
| Length | Strings Generated |
|---|---|
| 0 | ε |
| 1 | a, b |
| 3 | aaa, aba, bab, bbb |
| 5 | aabaa, ababa, baaab, bbabb |
| 7 | aaabaaa, aabbaa, abbbba, abbabba, baaaab, baabba, babbab, bbbabbb |
| 9 | aaaabaaaa, aaabbaaa, aabbbbaa, abbabbba, bbbbabbbb, etc. |
CFG for L = { wwᴿ ∪ w(a+b)wᴿ }
Let’s define the CFG for L = { wwᴿ ∪ w(a+b)wᴿ } through its 4 tuples G = (V, Σ, R, S)
-
Variables (V): {S}
-
Alphabet (Σ): {a, b}
-
Rules (R):
S → aSa | bSb | a | b | ε -
Start Symbol: S
The following diagram shows the CFG and the string “aabaa” derivation from L = { wwᴿ ∪ w(a+b)wᴿ }
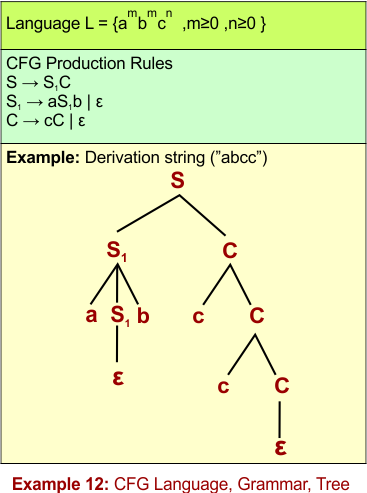
CFL Example 12: L = {ambmcn ,m≥0 ,n≥0 }
This language L = {ambmcn ,m≥0 ,n≥0 } consists of
- The number of
as andbs must be equal - The number of
cs is independent mcontrols theaandbbalancencontrols how manycs appear after
Valid Strings in L:
Let’s list possible strings for small values of m and n.
| m | n | String |
|---|---|---|
| 0 | 0 | ε (empty string) |
| 0 | 1 | c |
| 0 | 2 | cc |
| 1 | 0 | ab |
| 1 | 1 | abc |
| 1 | 2 | abcc |
| 2 | 0 | aabb |
| 2 | 1 | aabbc |
| 2 | 2 | aabbcc |
| 3 | 2 | aaabbbcc |
CFG for L = {ambmcn ,m≥0 ,n≥0 }
Let’s define the CFG for L = {ambmcn ,m≥0 ,n≥0 } through its 4 tuples G = (V, Σ, R, S)
-
Variables (V): {S, S1, C}
-
Alphabet (Σ): {a, b}
-
Rules (R):
S → S1CS1 → aS1b| εC → cC | ε -
Start Symbol: S
The following diagram shows the CFG and the string “abcc” derivation from L = {ambmcn ,m≥0 ,n≥0 }