Mealy to Moore Conversion

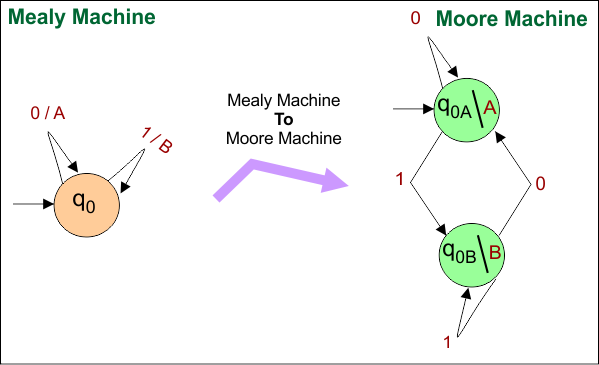
Mealy to Moore Conversion is slightly more complex than the conversion of Moore to Mealy machine. In a Mealy machine, the output depends on both the current state and the input, whereas in a Moore machine, the output is determined only by the current state. The following diagram represents the transition diagrams of Mealy and Moore machines.

In this lecture, we convert the Mealy Machine Transition diagram and transition table into an equivalent Moore Machine Diagram and transition table. First, look at some rules for Mealy to Moore conversions 

Mealy to Moore Conversion Algorithm

Step 01: Select the initial state of the Mealy machine and mark it as the initial state of the Moore machine.

Step 02: For each state (i.e., qx) in the Mealy machine, check how many different output symbols appear on all transitions entering that particular state (“qx”).

• Case 1: Exactly 1 output enters state “qx”
  • No duplication is required in the Moore machine.
  • The Moore state becomes: qx /A, where “A” is the single output associated with all transitions entering qx.
  • All input labels on transitions remain the same in Moore machines.
• Case 2: More than 1 output enters state “qx”
  • Suppose n different output symbols enter state qx.
  • Then you must create n separate Moore states for qx.
  • Example: If outputs A, B, C, D enter state qx, then you create: qx/A, qx/B, qx/C, and qx/D.
  • Each duplicated Moore state corresponds to one distinct output seen on transitions entering qx.
  • In a Moore machine, all input labels on transitions remain unchanged, like Mealy, while only the destination state names changed depending on the output.

Step 03: Ensure all states in Mealy machines follow step 02, for successful Mealy machine to Moore conversion.

Mealy to Moore Conversion – Transition Diagram

Two basic cases can be defined from conversions of Mealy’s transition diagram to Moore’s transition diagram.

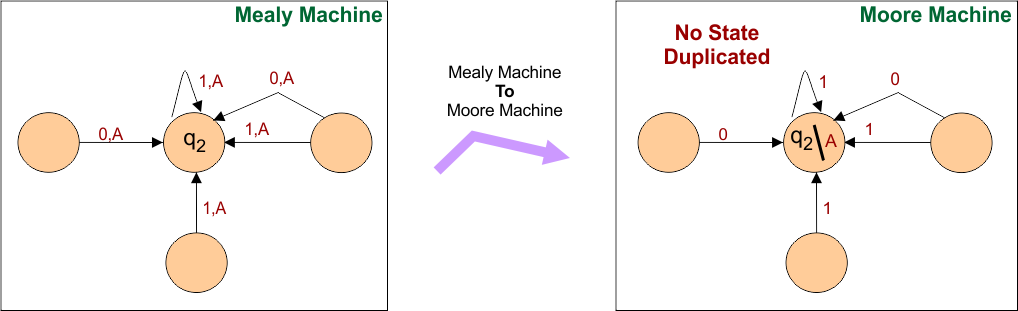
Case 01: No State Duplicated in Moore Machine

When every input that enters a Mealy state produces the same output. Then, simply place that output within that particular state of the Moore machine. In this case,  that particular state is not duplicated.

For Example

• Mealy Machine: When entering inputs are 5 (“0”, “0”, “1”, “0”, “1”) with all  similar outputs (i.e., “A”) in a particular state (i.e., say state “q2”)
• Moore Machine: In Mealy to Moore conversion, Particular State “q2” is not duplicated (because all provide similar outputs).

Case 02: States Duplicated in Moore Machine

When certain inputs are entered in a specific Mealy state, the outputs can vary. However, a Moore machine cannot represent multiple outputs within a single state. Therefore, that state must be duplicated “n” times, where “n” indicates the number of different output types.

For example, when “n = 3”

• Mealy Machine: When entering inputs are 5 (“0”, “0”, “1”, “0”, “1”) with 3 different outputs (i.e., “A”, “B”, “C”) in a particular state (i.e., say state “q2”)
• Moore Machine: In Mealy to Moore conversion, Particular State “q2” is duplicated 3 times (because outputs are 3 types), where new states become “q2A”, “q2B”, and “q2C” for output “A”, “B”, and “C” respectively.

Let’s explain some examples of Mealy to Moore Machine Conversions 

Mealy to Moore Conversion using Single-State Mealy

In this section, we will see some examples of Mealy to Moore conversions where only single state of Mealy machine is used to convert into Moore machine

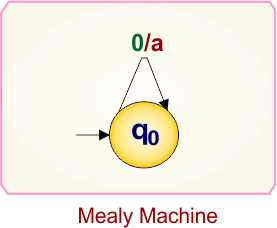
Example 1.1: Mealy to Moore conversion

Here is the single-state Mealy machine, which contains

• State: q0
• Input symbol: 0
• Output symbol: a

Let’s convert this Mealy Machine into a Moore Machine.

 

Step 01: Initial State

Mealy initial state = q0. So Moore’s initial state is also “q0” with an output.

Step 02: Count outputs entering at each state in Mealy

At state “q0” 

• From state “q0” on input “0” produce  output “a”

Step-2 Case-1:, Only a single output enters at state “q0”, which is “a”. Therefore, algorithm step-2, case-1 applies, state “q0” in Mealy does not duplicate, as given below

No more states found in the Mealy machine except “q0”. So, finally, the desired Moore Machine of example 1.1 is given below

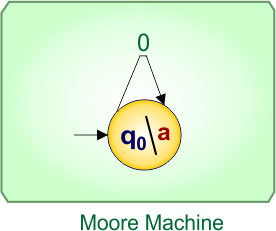
In Moore Machine,

• State: q0
• Input symbol: 0
• Output symbol: a

In Moore, input labels (0) on transitions (arrow) remain unchanged, like a Mealy machine, while only the destination state names change depending on the output.

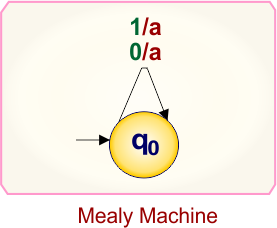
Example 1.2: Mealy to Moore conversion

Here is the single-state Mealy machine, which contains

• State: q0
• Input symbols: 0, 1
• Output symbols: a,b

Let’s convert this Mealy Machine into a Moore Machine.

Step 01: Initial State

Mealy initial state = q0. So Moore’s initial state is also “q0” with an output.

Step 02: Count outputs entering at each state in Mealy

At state “q0” 

• From state “q0” on input “0” produce  output “a”
• From state “q0” on input “1” produce  output “a”

Step-2 Case-1: So, only a single output enters at state “q0”, which is “a”. Therefore, algorithm step-2, case-1 applies, state “q0” in Mealy does not duplicate, as given below

No more states found in the Mealy machine except “q0”. So, finally, the desired Moore Machine of example 1.2 is given below

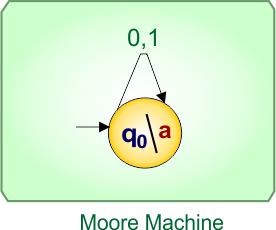
In Moore Machine,

• State: q0
• Input symbols: 0, 1
• Output symbols: a

In Moore, input labels (0,1) on transitions (arrow) remain unchanged, like a Mealy machine, while only the destination state names change depending on the output.

Example 1.3: Mealy to Moore conversion 

Here is the single-state Mealy machine, which contains

• State: q0
• Input symbols: 0, 1
• Output symbols: a,b

Let’s convert this Mealy Machine into a Moore Machine.

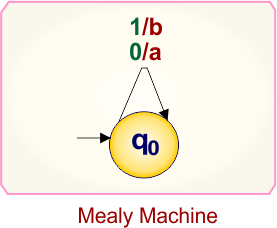
Step 01: Initial State

Mealy initial state = q0. So Moore’s initial state is also “q0” with an output.

Step 02: Count outputs entering at each state in Mealy

At state “q0” 

• From state “q0” on input “0” produce  output “a”
• From state “q0” on input “1” produce  output “b”

Step-2 Case-2: Two outputs entering at state “q0” are “a” and “b”. Therefore, algorithm step-2 case-2 applies, state “q0” in Mealy duplicated into two Moore states given below

• q0a/a

• q0b/b

No more states found in the Mealy machine except “q0”. So, finally, the desired Moore Machine of example 1.3 is given below

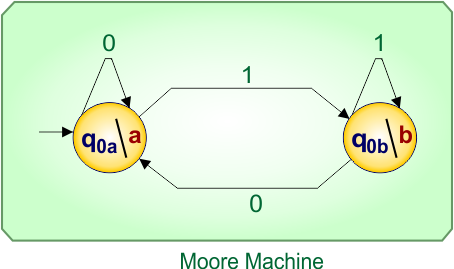
In Moore Machine,

• State: q0a, q0b
• Input symbols: 0, 1
• Output symbols: a,b

In Moore, all input labels (0,1) on transitions (arrow) remain unchanged, like a Mealy machine, while only the destination state names change depending on the output.

Example 1.4: Mealy to Moore conversion

Here is the single-state Mealy machine, which contains

• State: q0
• Input symbols: 0, 1, 10
• Output symbols: a,b, c

Let’s convert this Mealy Machine into a Moore Machine.

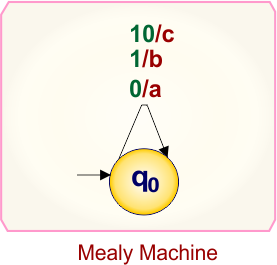
Step 01: Initial State

Mealy initial state = q0. So Moore’s initial state is also “q0” with an output.

Step 02: Count outputs entering at each state in Mealy

At state “q0” 

• From state “q0” on input “0” produce  output “a”
• From state “q0” on input “1” produce  output “b”
• From state “q0” on input “10” produce  output “c”

Step-2 Case-2: Three outputs entering at state “q0” which are “a”, “b” and “c”. Therefore, algorithm step-2 case-2 applies, state “q0” in Mealy duplicated into three Moore states given below

• q0a/a

• q0b/b

• q0c/c

No more states found in the Mealy machine except “q0”. So, finally, the desired Moore Machine of example 1.4 is given below 

In Moore Machine,

• State: q0a, q0b, q0c
• Input symbols: 0, 1, 10
• Output symbols: a,b, c

In Moore, all input labels on transitions remain unchanged, like Mealy, while only the destination state names change depending on the output.

Example 1.5: Mealy to Moore conversion

Here is the single-state Mealy machine, which contains

• State: q0
• Input symbols: 0, 1, 10, 11
• Output symbols: a,b, c,d

Let’s convert this Mealy Machine into a Moore Machine.

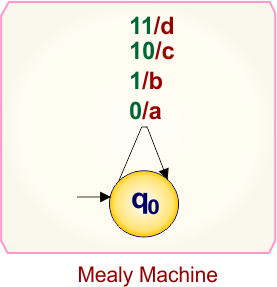
Step 01: Initial State

Mealy initial state = q0. So Moore’s initial state is also “q0” with an output.

Step 02: Count outputs entering at each state in Mealy

At state “q0” 

• From state “q0” on input “0” produce  output “a”
• From state “q0” on input “1” produce  output “b”
• From state “q0” on input “10” produce  output “c”
• From state “q0” on input “11” produce  output “d”

Step-2 Case-2: Four outputs entering at state “q0”, which are “a”, “b”, “c”, and “d”. Therefore, algorithm step-2 case-2 applies, state “q0” in Mealy duplicated into four Moore states given below

• q0a/a

• q0b/b

• q0c/c
• q0d/d

No more states found in the Mealy machine except “q0”. So, finally, the desired Moore Machine of example 1.5 is given below 

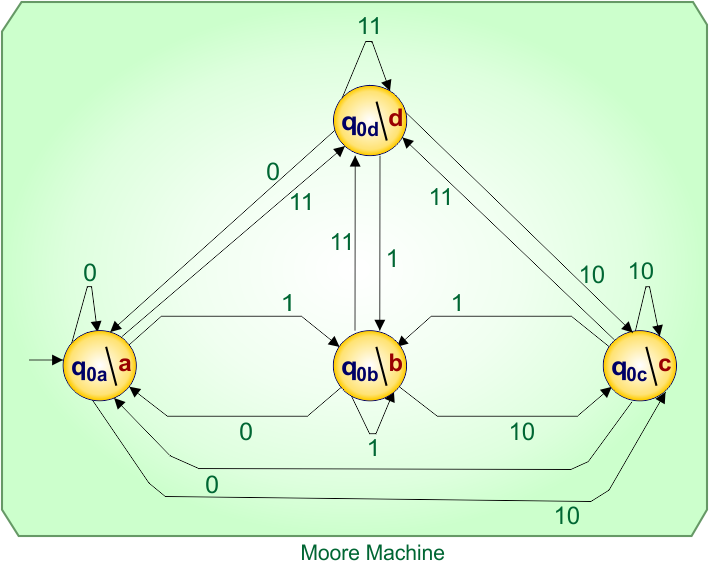
In Moore Machine,

• State: q0a, q0b, q0c, q0d
• Input symbols: 0, 1, 10,11
• Output symbols: a,b, c,d

In Moore, all input labels on transitions remain unchanged, like Mealy, while only the destination state names change depending on the output.

Example 1.6: Mealy to Moore conversion

Here is the single-state Mealy machine, which contains

• State: q0
• Input symbols: 0, 1, 10, 11, 100
• Output symbols: a,b, c,d

Let’s convert this Mealy Machine into a Moore Machine.

 

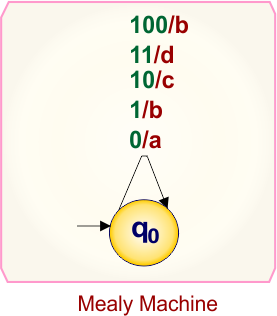
Step 01: Initial State

Mealy initial state = q0. So Moore’s initial state is also “q0” with an output.

Step 02: Count outputs entering at each state in Mealy

At state “q0” 

• From state “q0” on input “0” produce  output “a”
• From state “q0” on input “1” produce  output “b”
• From state “q0” on input “10” produce  output “c”
• From state “q0” on input “11” produce  output “d”
• From state “q0” on input “100” produce  output “b”

Step-2 Case-2: Four outputs entering at state “q0”, which are “a”, “b”, “c”, and “d”. Therefore, the algorithm step-2 case-2 applies, state “q0” in Mealy duplicated into four Moore states given below

• q0a/a
• q0b/b
• q0c/c
• q0d/d

No more states found in the Mealy machine except “q0”. So, finally, the desired Moore Machine of example 1.6 is given below 

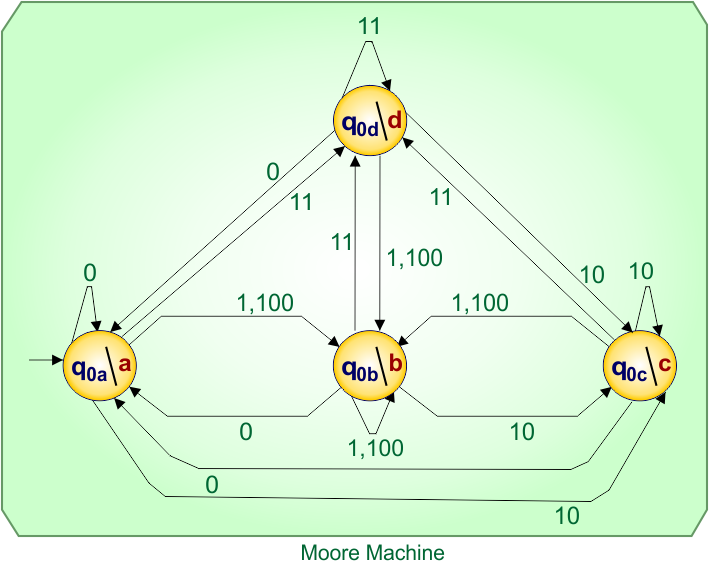
In Moore Machine,

• State: q0a, q0b, q0c, q0d
• Input symbols: 0, 1, 10,11, 100
• Output symbols: a,b, c,d

In Moore, all input labels on transitions remain unchanged, like Mealy, while only the destination state names change depending on the output.

Mealy to Moore Conversion using two-State Mealy

In this section, we will see some examples of Mealy to Moore conversions where only two states of Mealy machine are used to convert into Moore machine

Example 2.1: Mealy to Moore conversion

Here is the single-state Mealy machine, which contains

• States: q0,q1
• Input symbol: 0,1
• Output symbol: a,b

Let’s convert this Mealy Machine into a Moore Machine.

Step 01: Initial State

Mealy initial state = q0. So Moore’s initial state is also “q0” with an output.

Step 02: Count outputs entering at each state in Mealy

At state “q0” 

• From state “q0” on input “0” produce  output “a”

Step-2 Case-1: only single output entering at state “q0”, which is  “a”. Therefore, the algorithm step-2 case-1 applies, state “q0” in Mealy remains “q0” in Moore, no duplication needed

At state “q1” 

• From state “q0” on input “1” produce  output “b”
• From state “q1” on input “0” produce  output “b”
• From state “q1” on input “1” produce  output “b”

Step-2 Case-1: only single output entering at state “q1”, which is  “a”. Therefore, the algorithm step-2 case-1 applies, state “q1” in Mealy remains “q1” in Moore, no duplication needed

No more states found in the Mealy machine except “q0”. So, finally, the desired Moore Machine of example 2.1 is given below 

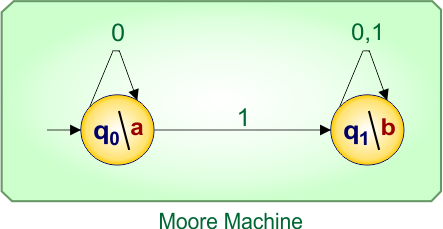
In Moore Machine,

• States: q0, q1
• Input symbols: 0, 1
• Output symbols: a,b

In Moore, all input labels on transitions remain unchanged, like Mealy, while only the destination state names change depending on the output.

Example 2.2: Mealy to Moore conversion

Here is the single-state Mealy machine, which contains

• States: q0,q1
• Input symbol: 0,1
• Output symbol: a,b

Let’s convert this Mealy Machine into a Moore Machine.

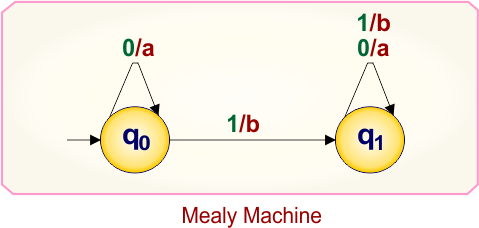
At state “q0” 

• From state “q0” on input “0” produce  output “a”

Step-2 Case-1: only single output entering at state “q0”, which is  “a”. Therefore, the algorithm step-2 case-1 applies, state “q0” in Mealy remains “q0” in Moore, no duplication needed

At state “q1” 

• From state “q0” on input “1” produce  output “b”
• From state “q1” on input “0” produce  output “a”
• From state “q1” on input “1” produce  output “b”

Step-2 Case-2: Two outputs entering at state “q1”, which are “a” and “b”. Therefore, the algorithm step-2 case-2 applies, state “q0” in Mealy duplicated into two Moore states given below

• q1a/a
• q1b/b

No more states found in the Mealy machine. So, finally, the desired Moore Machine of example 2.2 is given below 

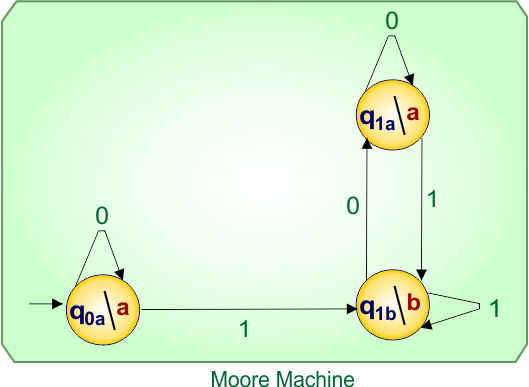
In Moore Machine,

• States: q0a, q1b, q1a
• Input symbols: 0, 1
• Output symbols: a,b

In Moore, all input labels on transitions remain unchanged, like Mealy, while only the destination state names change depending on the output.

Example 2.3: Mealy to Moore conversion

Here is the single-state Mealy machine, which contains

• States: q0,q1
• Input symbol: 0,1, 10
• Output symbol: a,b,c

Let’s convert this Mealy Machine into a Moore Machine.

 

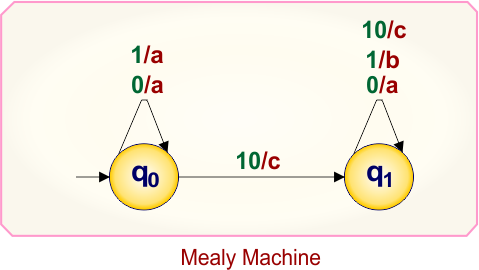
At state “q0” 

• From state “q0” on input “0” produce  output “a”
• From state “q0” on input “1” produce  output “a”

Step-2 Case-1: only single output entering at state “q0”, which is  “a”. Therefore, the algorithm step-2 case-1 applies, state “q0” in Mealy remains “q0” in Moore, no duplication needed

At state “q1” 

• From state “q0” on input “10” produce  output “c”
• From state “q1” on input “0” produce  output “a”
• From state “q1” on input “1” produce  output “b”
• From state “q1” on input “10” produce  output “c”

Step-2 Case-2: Three outputs enter state “q1”: “a”, “b”, and “c”. Therefore, the algorithm step-2 case-2 applies, state “q1” in Mealy duplicated into two Moore states given below

• q1a/a
• q1b/b
• q1c/c

No more states found in the Mealy machine. So, finally, the desired Moore Machine of example 2.3is given below 

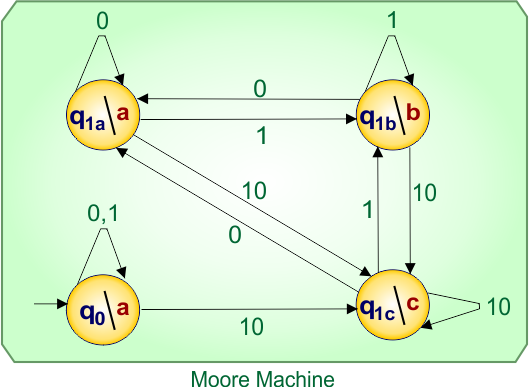
In Moore Machine,

• States: q0, q1a, q1b, q1c
• Input symbols: 0, 1, 10
• Output symbols: a,b,c

In Moore, all input labels on transitions remain unchanged, like Mealy, while only the destination state names change depending on the output.

Mealy to Moore Conversion Using 3 Mealy States 

In this section, we will see some examples of Mealy to Moore conversions where only three states of Mealy machine are used to convert into Moore machine

Example 3.1: Mealy to Moore conversion

Here is the single-state Mealy machine, which contains

• States: q0,q1, q2
• Input symbol: 0,1
• Output symbol: a,b

Let’s convert this Mealy Machine into a Moore Machine.

Step 01: Initial State

Mealy initial state = q0. So Moore’s initial state is also “q0” with an output.

Step 02: Count outputs entering at each state in Mealy

At state “q0” 

• From state “q0” on input “0” produce  output “a”

Step-2 Case-1: only single output entering at state “q0”, which is  “a”. Therefore, the algorithm step-2 case-1 applies, state “q0” in Mealy remains “q0” in Moore, no duplication needed

At state “q1” 

• From state “q0” on input “1” produce  output “b”
• From state “q1” on input “0” produce  output “b”

Step-2 Case-1: only single output entering at state “q1”, which is  “b”. Therefore, the algorithm step-2 case-1 applies, state “q1” in Mealy remains “q1” in Moore, no duplication needed

At state “q2” 

• From state “q1” on input “1” produce  output “b”
• From state “q2” on input “0” produce  output “b”
• From state “q2” on input “1” produce  output “b”

Step-2 Case-1: only single output entering at state “q2”, which is  “b”. Therefore, the algorithm step-2 case-1 applies, state “q2” in Mealy remains “q2” in Moore, no duplication needed

No more states found in the Mealy machine. So, finally, the desired Moore Machine of example 3.1 is given below 

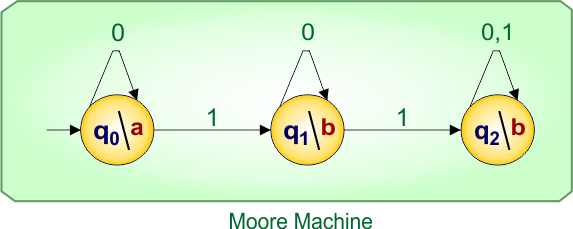
In Moore Machine,

• States: q0, q1, q2
• Input symbols: 0, 1
• Output symbols: a,b

In Moore, all input labels on transitions remain unchanged, like Mealy, while only the destination state names change depending on the output.

Example 3.2: Mealy to Moore conversion

Here is the single-state Mealy machine, which contains

• States: q0,q1,q2
• Input symbol: 0,1
• Output symbol: a,b

Let’s convert this Mealy Machine into a Moore Machine.

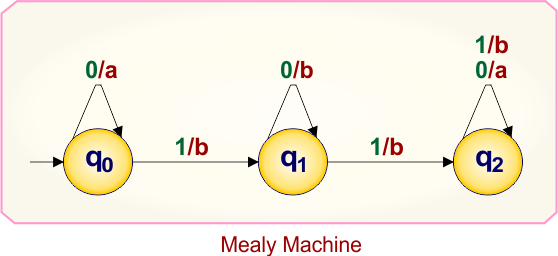
At state “q0” 

• From state “q0” on input “0” produce  output “a”

Step-2 Case-1: only single output entering at state “q0”, which is  “a”. Therefore, the algorithm step-2 case-1 applies, state “q0” in Mealy remains “q0” in Moore, no duplication needed

At state “q1” 

• From state “q0” on input “1” produce  output “b”
• From state “q1” on input “0” produce  output “b”

Step-2 Case-1: only single output entering at state “q1”, which is  “b”. Therefore, the algorithm step-2 case-1 applies, state “q1” in Mealy remains “q1” in Moore, no duplication needed

At state “q2” 

• From state “q1” on input “1” produce  output “b”
• From state “q2” on input “0” produce  output “a”
• From state “q2” on input “1” produce  output “b”

Step-2 Case-2: Two outputs entering at state “q2”, which are “a” and “b”. Therefore, the algorithm step-2 case-2 applies, state “q2” in Mealy duplicated into two Moore states given below

• q2a/a
• q2b/b

No more states found in the Mealy machine. So, finally, the desired Moore Machine of example 2.2 is given below 

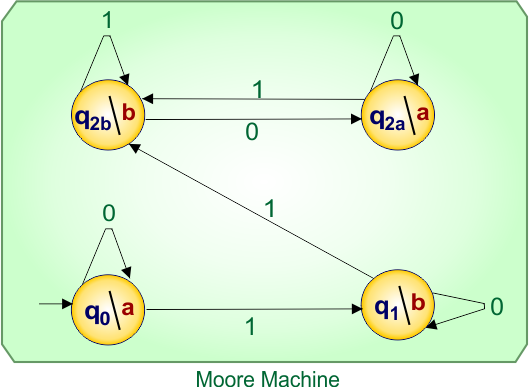
In Moore Machine,

• States: q0, q1, q2a, q2b
• Input symbols: 0, 1
• Output symbols: a,b

In Moore, all input labels on transitions remain unchanged, like Mealy, while only the destination state names change depending on the output.

Example 3.3: Mealy to Moore conversion

Here is the single-state Mealy machine, which contains

• States: q0,q1,q2
• Input symbol: 0,1, 10
• Output symbol: a,b,c

Let’s convert this Mealy Machine into a Moore Machine.

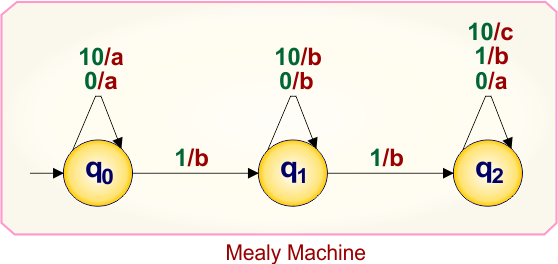
At state “q0” 

• From state “q0” on input “0” produce  output “a”
• From state “q0” on input “10” produce  output “a”

Step-2 Case-1: only single output entering at state “q0”, which is  “a”. Therefore, the algorithm step-2 case-1 applies, state “q0” in Mealy remains “q0” in Moore, no duplication needed

At state “q1” 

• From state “q0” on input “1” produce  output “b”
• From state “q1” on input “0” produce  output “b”
• From state “q1” on input “10” produce  output “b”

Step-2 Case-1: only single output entering at state “q1”, which is  “b”. Therefore, the algorithm step-2 case-1 applies, state “q1” in Mealy remains “q1” in Moore, no duplication needed

At state “q2” 

• From state “q1” on input “1” produce  output “b”
• From state “q2” on input “0” produce  output “a”
• From state “q2” on input “1” produce  output “b”
• From state “q2” on input “10” produce  output “c”

Step-2 Case-2: three outputs entering at state “q2”, which are “a”, “b”, and “c”. Therefore, the algorithm step-2 case-2 applies, state “q2” in Mealy duplicated into two Moore states given below

• q2a/a
• q2b/b
• q2c/c

No more states found in the Mealy machine. So, finally, the desired Moore Machine of example 2.2 is given below 

In Moore Machine,

• States: q0, q1, q2a, q2b, q2c
• Input symbols: 0, 1, 10
• Output symbols: a,b, c

In Moore, all input labels on transitions remain unchanged, like Mealy, while only the destination state names change depending on the output.

Example 3.4: Mealy to Moore conversion

Here is the single-state Mealy machine, which contains

• States: q0,q1,q2
• Input symbol: 0,1, 10
• Output symbol: a,b,c

Let’s convert this Mealy Machine into a Moore Machine.

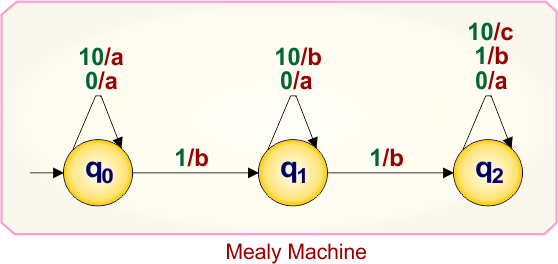
At state “q0” 

• From state “q0” on input “0” produce  output “a”
• From state “q0” on input “10” produce  output “a”

Step-2 Case-1: only single output entering at state “q0”, which is  “a”. Therefore, the algorithm step-2 case-1 applies, state “q0” in Mealy remains “q0” in Moore, no duplication needed

At state “q1” 

• From state “q0” on input “1” produce  output “b”
• From state “q1” on input “0” produce  output “a”
• From state “q1” on input “10” produce  output “b”

Step-2 Case-2: two outputs entering at state “q1”, which are “a” and “b”. Therefore, the algorithm step-2 case-2 applies, state “q1” in Mealy duplicated into two Moore states given below

• q1a/a
• q1b/b

At state “q2” 

• From state “q1” on input “1” produce  output “b”
• From state “q2” on input “0” produce  output “a”
• From state “q2” on input “1” produce  output “b”
• From state “q2” on input “10” produce  output “c”

Step-2 Case-2: three outputs entering at state “q2”, which are “a”, “b”, and “c”. Therefore, the algorithm step-2 case-2 applies, state “q2” in Mealy duplicated into two Moore states given below

• q2a/a
• q2b/b
• q2c/c

No more states found in the Mealy machine. So, finally, the desired Moore Machine of example 2.2 is given below 

In Moore Machine,

• States: q0, q1a, q1b, q2a, q2b, q2c
• Input symbols: 0, 1, 10
• Output symbols: a,b, c

In Moore, all input labels on transitions remain unchanged, like Mealy, while only the destination state names change depending on the output.

Mealy to Moore Conversion [Shortcut Method]

Here we explain some examples of Mealy to moore conversion without detail conversion process

Mealy to Moore Conversion Example 01

In this example,

• Mealy Machine: Two inputs “0” and “1” with different outputs “A” and “B” enter into a state “q0”.
• Moore Machine: State “q0” is duplicated where new states become “q0A” and “q0B” for output “A” and “B” respectively

as shown in the following diagram.

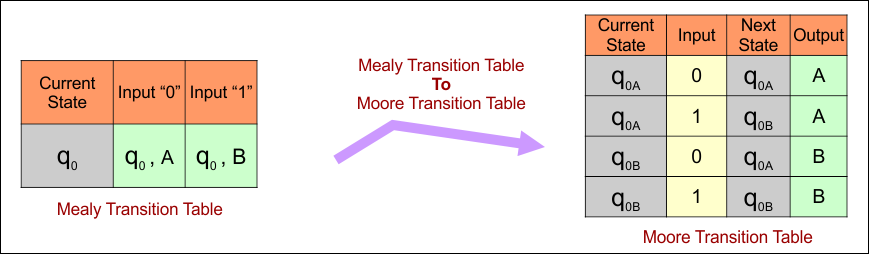
Mealy to Moore conversion, the transition table is given below

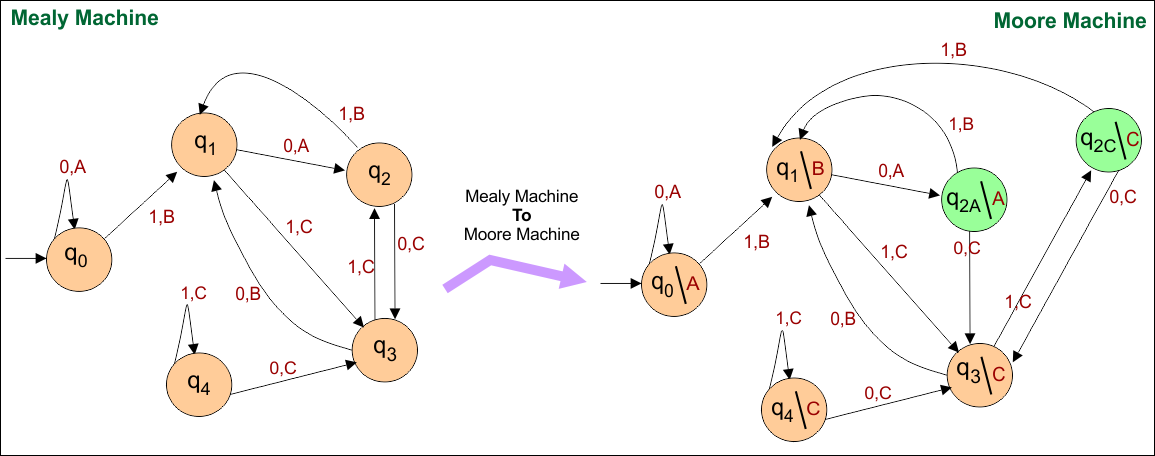
Mealy to Moore Conversion Example 02

In this example,

• Mealy Machine: Two inputs (“0” and “1”) with different outputs (“A” and “C”) enter into a state “q2”.
• Moore Machine: State “q2” is duplicated where new states become “q2A” and “q2C” for output “A” and “C” respectively

As shown in the following diagram.

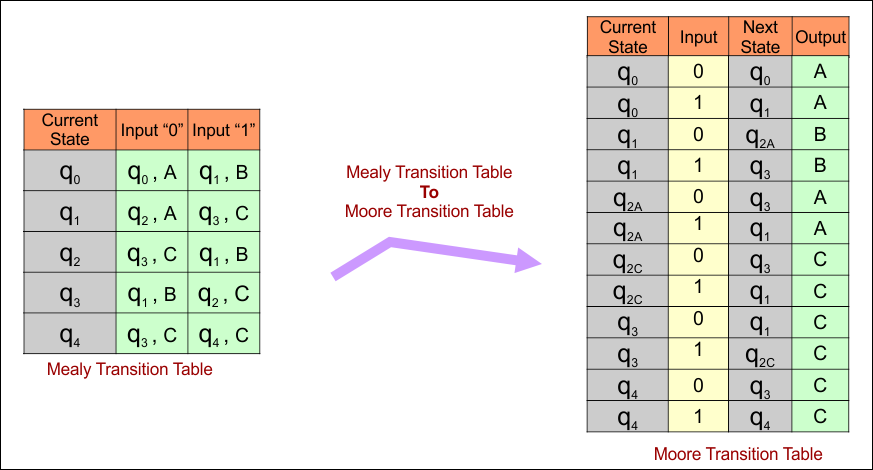
Mealy to Moore conversion, the transition table is given below

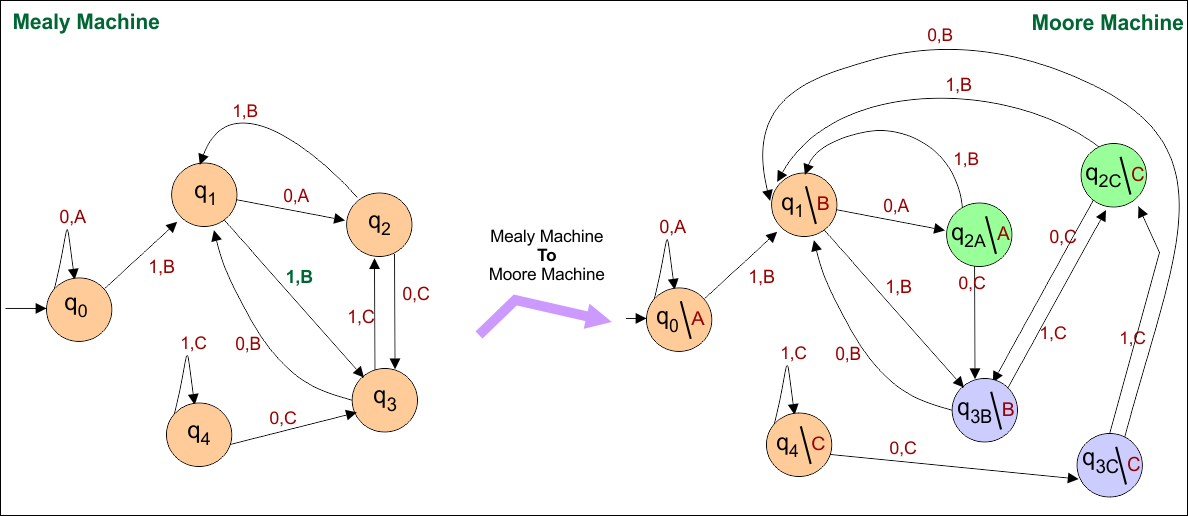
Mealy to Moore Conversion Example 03

In this example, for state “q2”

• Mealy Machine: Two inputs (“0” and “1”) with different outputs (“A” and “C”) enter into a state “q2”.
• Moore Machine: State “q2” is duplicated twice where new states becomes “q2A” and “q2C” for output “A” and “C” respectively

Similarly, for state “q3”

• Mealy Machine: Three inputs (“0″, 0” and “1”) with two different types of outputs (“B” and “C”) enter into a state “q3”.
• Moore Machine: State “q3” is duplicated twice where new states becomes “q3B” and “q3C” for output “B” and “C” respectively

As shown in the following diagram.

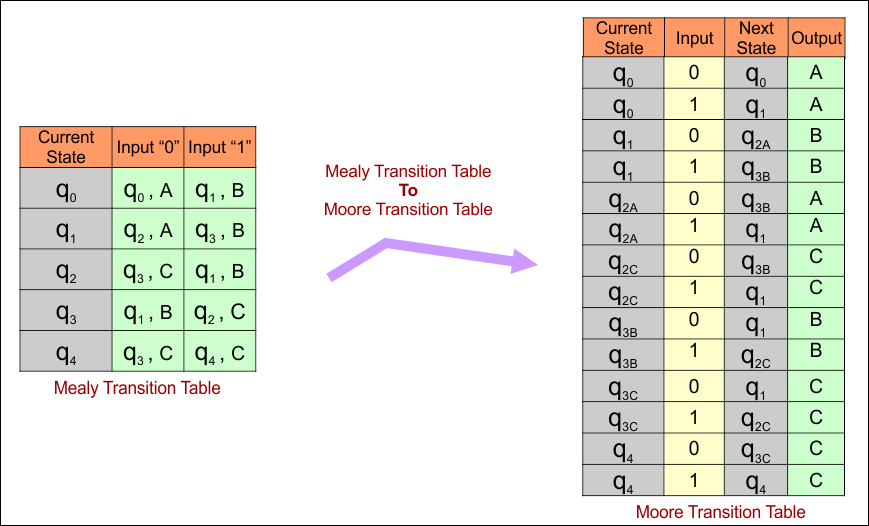
Mealy to Moore conversion, the transition table is given below

Mealy to Moore Conversion Example 04

In this example, for state “q2”

• Mealy Machine: Three inputs (“0”, “0” and “1”) with three different outputs (“A”, “B” and “C”) enter into a state “q2”.
• Moore Machine: State “q2” is  duplicated (3 times) where new states becomes “q2A”, “q2B” and “q2C” for output “A”, “B” and “C” respectively

As shown in the following diagram.

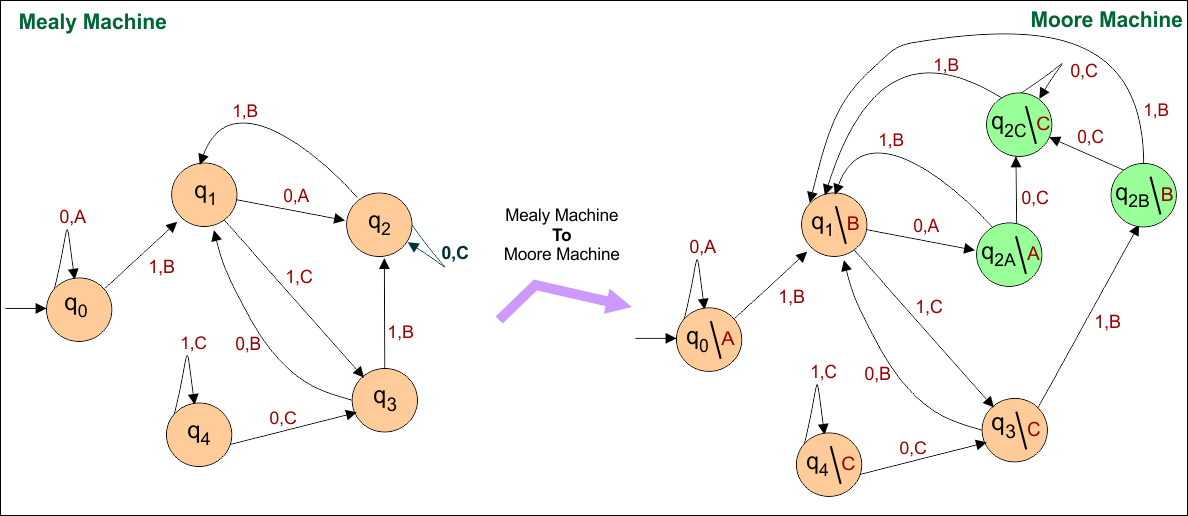
Mealy to Moore conversion, the transition table is given below

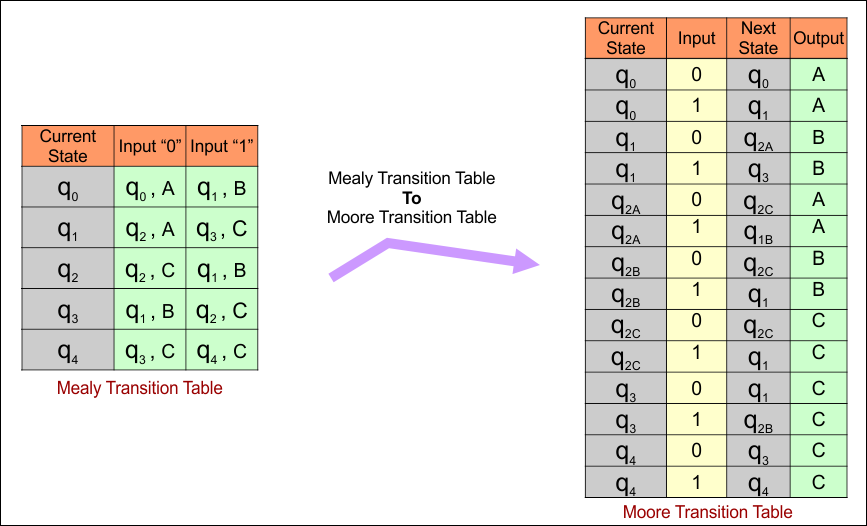
Mealy to Moore Conversion Example 05

In this example, for state “q4”

• Mealy Machine: Four inputs (“0”, “1”, “1”, and “1”) with four different outputs (“A”, “B”, “C”, and “C”) enter into a state “q4”.
• Moore Machine: State “q2” is  duplicated (4 times) where new states become “q4A”, “q4B”, “q4C”, and “q4D” for output “A”, “B”, “C”, and “D” respectively

As shown in the following diagram.

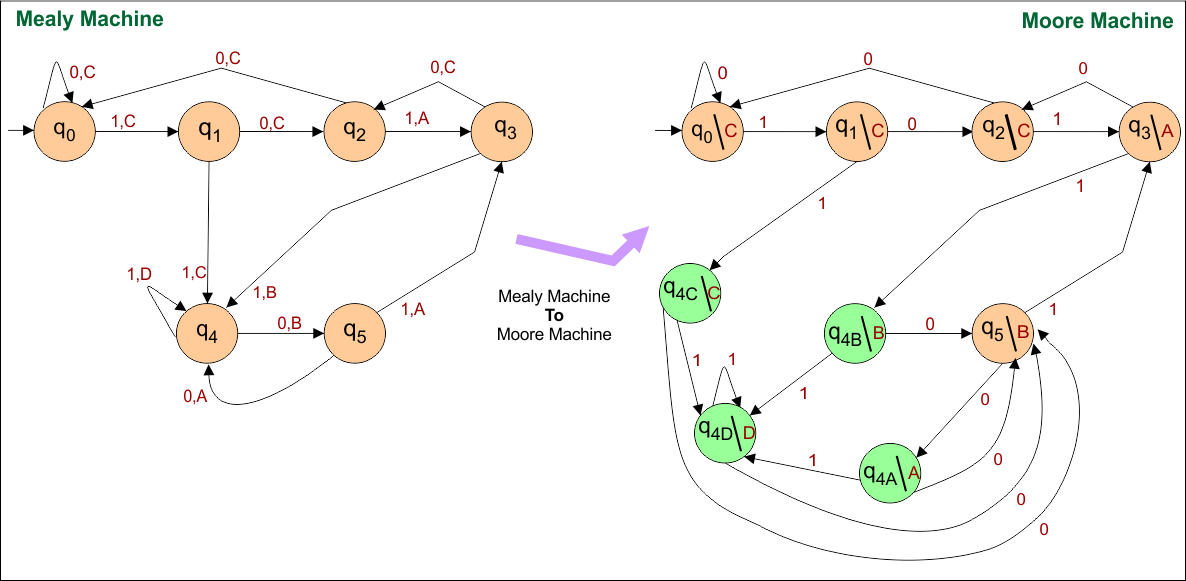
Mealy to Moore conversion, the transition table is given below

 

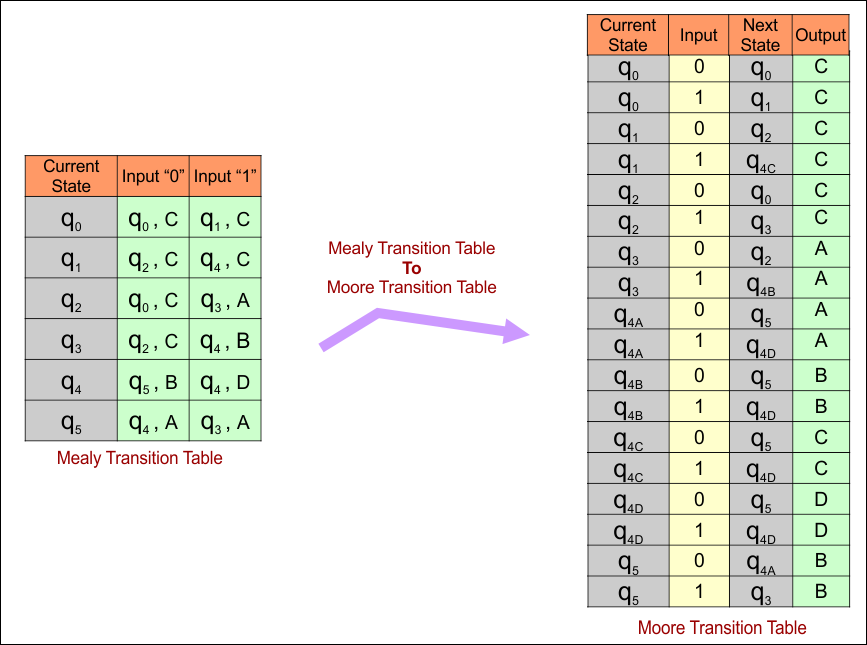
Mealy to Moore Conversion – Transition Table

Two basic cases can be defined from conversions of Mealy’s transition table to Moore’s transition Table.

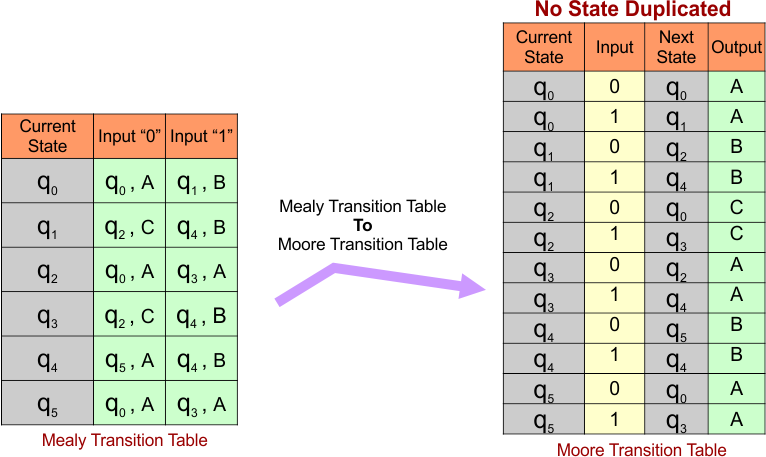
Case  01: No State Duplicated in Moore Machine

When a particular state appears once or more than once in the “input column” with a similar output of the Mealy Transition Table, then that particular state also appears the same in the Moore Transition Table (never duplicated).

Example: In the following transition table, both input columns (for “0” and “1”) display the next state along with the output.

• All “q0” states, either in input “0” or “1” columns, contain output “A” (mentioned as qo, A)
• All “q1” states, either in input “0” or “1” columns, contain output “B” (mentioned as q1, B)
• All “q2” states, either in input “0” or “1” columns, contain output “C” (mentioned as q2, C)
• All “q3” states, either in input “0” or “1” columns, contain output “A” (mentioned as q3, A)
• All “q4” states, either in input “0” or “1” columns, contain output “B” (mentioned as q4, B)
• All “q5” states, either in input “0” or “1” columns, contain output “A” (mentioned as q5, A)

So, the No Input state in the input columns holds different types of output.  The following figure shows all

Case 02: State Duplicated in Moore Machine

When a particular state appears more than once in the input column with different outputs (i.e,. “A”, B etc) of the Mealy Transition Table, then that particular state will always be duplicated “n” times in the Moore Transition Table, where “n” represents how many types of output. 

Example: In the following transition table, both input columns (for “0” and “1”) display the next state along with the output. All “q0” states, either in input “0” or “1” columns, contain output “A” (mentioned as qo, A). No “q0” state is duplicated. All “q1” states, either in input “0” or “1” columns, contain output “B” (mentioned as q1, B). No “q1” state is duplicated. All “q2” states, either in input “0” or “1” columns, contain output  “A” and”C” (mentioned as q2, A, q2, C). So, “q2” is duplicated. All “q3” states, either in input “0” or “1” columns, contain output “B” and “C” (mentioned as q3, B and q3, C). So,  “q3” is duplicated. All “q4” states, either in input “0” or “1” columns, contain output “C” (mentioned as q4, C).  No “q4” state is duplicated. So, the No Input state in the input columns holds different types of output.  The following figure shows all

Mealy to Moore Conversion [Easiest way]

Example 01: Single State with two inputs

Consider the following Mealy Machine

As in the above Mealy Machine,

• The start state is q0, and it receives inputs of 0 and 1, both resulting in the output “a.” Whenever either input is received in state q0, the output is consistently “a.” Therefore, you can remove the output “a” from the transition arrows and display it alongside the state q0. It becomes a Moore machine.

Finally, the Moore Machine is given under

Example 02: Three States with two inputs

Consider the following Mealy Machine

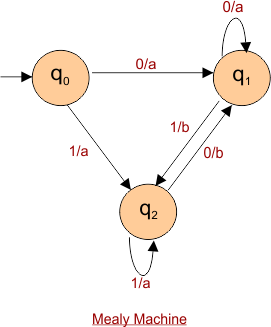
Mealy to Moore conversion Start at state “q0”

At State “q0”, there is no arrow entering into the state q0. So, the output for “q0” is null. As given Below

At state q1,

Three arrows are leading into state q1. The arrows from states q0 and q1 have an input of “0” that produces an output of “a,” while the arrow from state q2 has an input of “0” that produces an output of “b.“

Since there are two types of outputs (a and b) entering state q1, a duplicate of q1 is created with a different output. The output of type “a” is associated with state “q1/a, while the output of type “b” is linked to the duplicated state “q1/b”, as shown below.

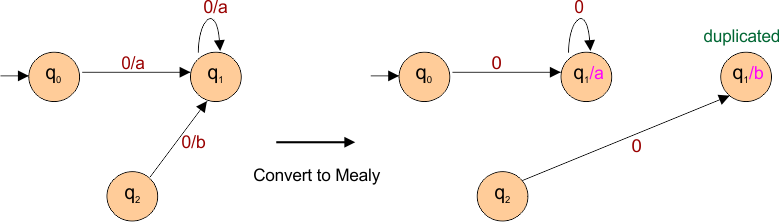
Transitions from both states  q1/a and q1/b are

• For input “0” transition goes to q1 for output “a”.
• For input “1”, the transition goes to q2 for output “b”.

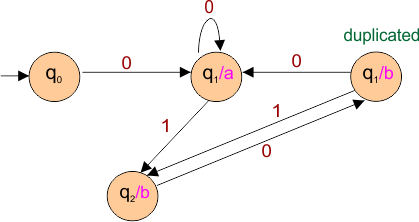
At state “q2.”

• Three arrows are entering the state q2. Arrows from q0 and q2 (itself) have the input “0” with output “a”, and the Arrow from q1 has the input “1” with “b” output. Output of 2 types (“a” and “b”) is entered into state q2, So One duplicate state of q2 is generated.
• By completing the transition from both states (original q2/a and duplicate q2/b) for inputs 0 and 1 (similarly as q1/a and q1/b), the final Mealy machine is given below.

Important: After State duplication in the transition diagram q1 is named as q1a and q1b, Similary, q2 is named as q2a and q2b

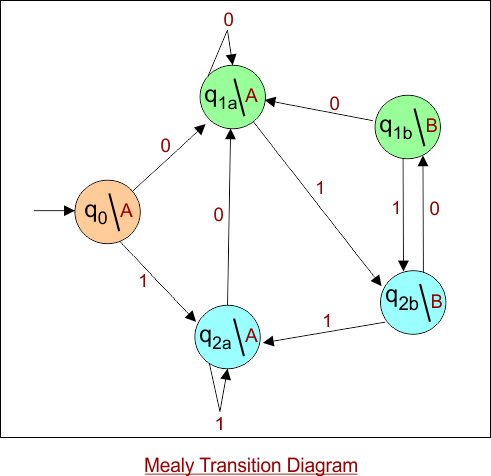
Note: The output from the initial state “q0” is mentioned as “A”. This is output “A” is because no transitions lead into state “q0”, we seclect output from those transitions going away from “q0”.

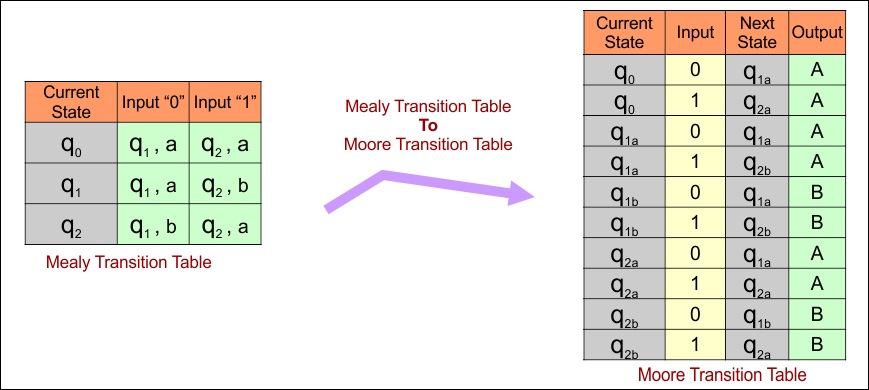
Mealy to Moore conversion, the transition table for the given example is given below

Examination-Based Question

In examination-based questions related to Mealy to Moore machine conversion, a possible case to solve is one of the following.

• Mealy Machine Diagram  → Moore Machine Diagram
• Mealy Transition Table → Moore Transition Table
• Mealy Machine Diagram → Mealy Transition Table → Moore Transition Table → Moore Diagram

Important. If “M” is the number of states and “N” is the number of outputs in the Mealy Machine, then the maximum number of States in the Mealy Machine will be “M” multiplied by “N”. Suppose if 3 number of states and 2 number of outputs in Mealy, then 6 will be the maximum state in Moore Machine.