Difference Between BST, M-Way, and B-Tree
BST (Binary Search Tree) is the foundation of an M-Way Search Tree and M-Way is the foundation of a B Tree.
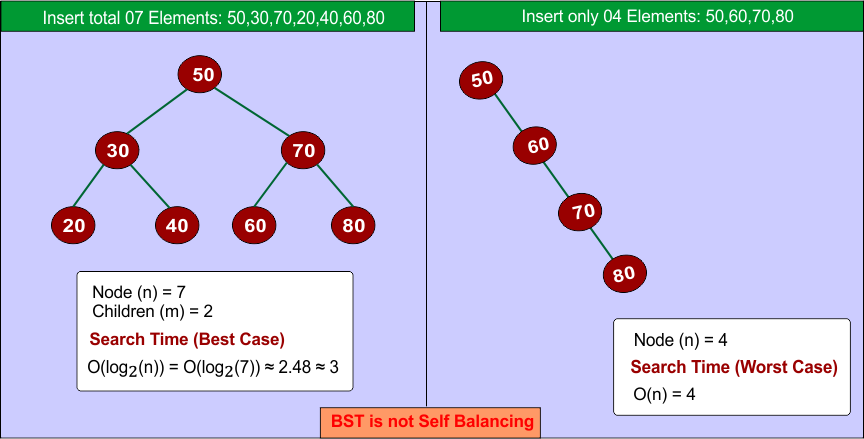
A Binary Search Tree (BST) is not self-balancing and can have a maximum of two children per node. Similarly, an M-Way tree is also not self-balancing and can hold a maximum of “M” children per node. In contrast, a B-tree is a self-balancing tree that can accommodate between ⌈M/2⌉ and M children per node.
| Important: A balanced search tree maintains a nearly equal number of nodes on both sides. |
1. Binary Search Tree (BST)
- Each node has at most 2 children (left and right).
- It may become unbalanced, leading to an inefficient O(N) search in the worst case.
- Insertions and deletions may require tree rotations to maintain balance (e.g., AVL, Red-Black trees).
- Used in in-memory searching, sorting, and dynamic set operations.
2. M-Way Tree
- Each node can have up to M children, generalizing the BST structure.
- Not necessarily balanced, but allows multi-way branching for faster access.
- Used in applications like trie structures, file indexing, and decision trees.
- Searching is faster than BST since each node can store multiple keys.

3. B-Tree
- A balanced M-Way search tree, ensuring logarithmic height O(log M N).
- Each node contains between ⌈M/2⌉ and M children, preventing skewed growth.
- Insertions and deletions involve node splitting and merging to maintain balance.
- Used in databases, file systems, and indexing due to efficient disk-based operations.

Time Complexity Table
| Tree Type | Worst Case Search Time | Best Case Search Time | Balanced? |
|---|---|---|---|
| BST (Skewed) | O(n) (if unbalanced) | O(log₂(n)) (if balanced) | May or may not |
| M-Way Search Tree | O(n) (if unbalanced) | O(logₘ(n)) (if balanced) | May or may not |
| B-Tree | O(logₘ(n)) | O(logₘ(n)) | Always |
where
- m = maximum number of children per node (order of the tree)
- n = number of elements in the tree













