Infix to Prefix Conversion Using Stack

Step 01: Initialize

• Create an empty stack.
• Reverse the infix expression.
  • Swap the left parenthesis ( with the right parenthesis ) and vice versa.
• Start scanning the reversed expression from left to right.

Step 02: For each symbol in the expression

• If the symbol is an operand:
  • Append that operand to the output.
• If the symbol is a left parenthesis (:
  • Push it onto the stack.
• If the symbol is a right parenthesis ):
  • Pop operators from the stack and append them to the output until a left parenthesis ( is encountered.
  • Discard both the left and right parentheses.
• If the symbol is an operator:
  • If the stack is not empty and the precedence of the operator on top of the stack is greater than or equal to the current operator:
    • Pop the operators from the stack and append them to the output.
  • Otherwise (else part): Push the current operator onto the stack.

Step 03: After scanning all the symbols

• Pop any remaining operators from the stack and and append it to output.

Step 04: Final Step

• Reverse the output of step 03 to get the prefix expression.

The following diagram will explain it in detail

Example: Infix expression 7 + 5 * 3 / 5 ^ 1 + (3 - 2)

Step 01: Reverse the Expression

Reversing the original expression and swapping parentheses:

• Original expression: 7 + 5 * 3 / 5 ^ 1 + (3 - 2)
• Reversed expression: ( 2 - 3 ) + 1 ^ 5 / 3 * 5 + 7

the following diagram shows that how to reverse the original infix expression

Step 02: Apply Infix-to-Postfix Conversion on the Reversed Expression

Now we will scan the reversed infix expression ( 2 - 3 ) + 1 ^ 5 / 3 * 5 + 7

Initialization

• Stack = []
• Output = []

Step-by-Step Processing of the Reversed Expression

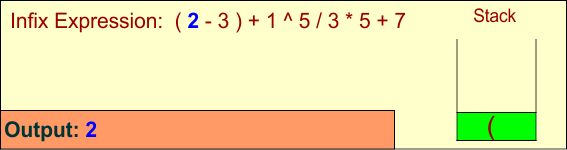
Symbol: (
Operator: Push onto the stack.
Stack: ['('], Output: []

Symbol: 2
Operand: Append to the output.
Stack: ['('], Output: ['2']

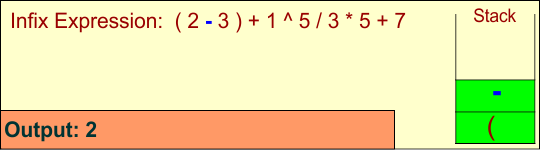
Symbol: -
Operator: Push onto the stack.
Stack: ['(', '-'], Output: ['2']

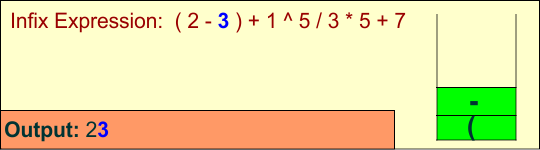
Symbol: 3
Operand: Append to the output.
Stack: ['(', '-'], Output: ['2', '3']

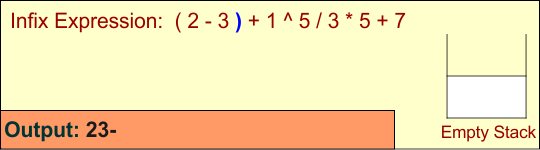
Symbol: )
Operator: Pop from the stack until ( is encountered.
Pop - and append it to the output, then discard the parentheses.
Stack: [], Output: ['2', '3', '-']

Symbol: +
Operator: Push onto the stack.
Stack: ['+'], Output: ['2', '3', '-']

Symbol: 1
Operand: Append to the output.
Stack: ['+'], Output: ['2', '3', '-', '1']

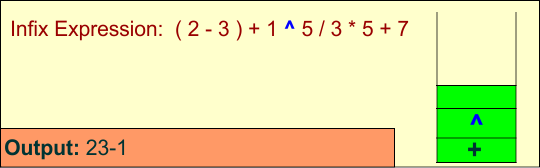
Symbol: ^
Operator: Push onto the stack.
Stack: ['+', '^'], Output: ['2', '3', '-', '1']

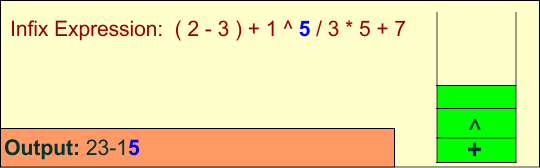
Symbol: 5
Operand: Append to the output.
Stack: ['+', '^'], Output: ['2', '3', '-', '1', '5']

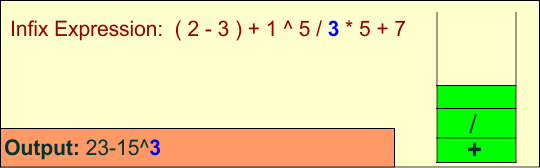
Symbol: /
Operator: Pop ^first (because it has higher precedence) from the stack and append it to the output.
Push / onto the stack.
Stack: ['+', '/'], Output: ['2', '3', '-', '1', '5', '^']

Symbol: 3
Operand: Append to the output.
Stack: ['+', '/'], Output: ['2', '3', '-', '1', '5', '^', '3']

Symbol: *
Operator: Push * onto the stack.
Stack: ['+', '/', '*'], Output: ['2', '3', '-', '1', '5', '^', '3']

Symbol: 5
Operand: Append to the output.
Stack: ['+', '/', '*'], Output: ['2', '3', '-', '1', '5', '^', '3', '5']

Symbol: +
Operator: Pop all operators of equal or higher precedence (*, /) from the stack and append them to the output.
Push + onto the stack. Note: if the same operator occurs as (+), push it into the stack over the previous +.
Stack: ['+', '+'], Output: ['2', '3', '-', '1', '5', '^', '3', '5', '*', '/']

Symbol: 7
Operand: Append to the output.
Stack: ['+','+'], Output: ['2', '3', '-', '1', '5', '^', '3', '5', '*', '/', '7']

Step 03: Pop Remaining Operators

Pop the remaining operators from the stack and append them to the output.
Stack: [], Output: ['2', '3', '-', '1', '5', '^', '3', '5', '*', '/', '7', '+', '+']

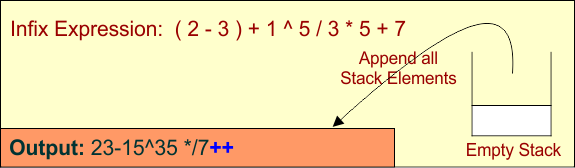
Step 03 provides the postfix notation: 2 3 – 1 5 ^ 3 5 * / 7 + +

Step 04: Reverse the Output of Step 03

Reverse the output of step 03 to get the final prefix expression.

+ + 7 / * 5 3 ^ 5 1 - 3 2


This is the required prefix expression for the given infix expression 7 + 5 * 3 / 5 ^ 1 + (3 - 2).