Insertion in B Tree with Examples (Order 3, 4)

Insertion in a B-tree means adding elements while keeping the tree balanced. A B-tree is a self-balancing search tree that maintains sorted data and ensures efficient searching, insertion, and deletion.

This lecture will explain the insertion process with a straightforward example. You will observe how nodes split and adjust to maintain the properties of the B-tree. Let’s get started!

Node Structure

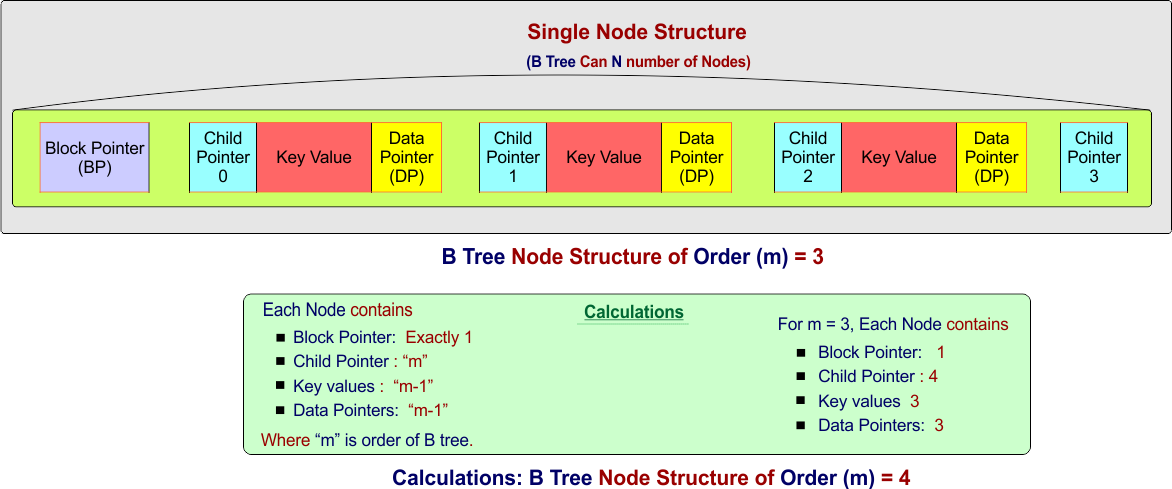
Node Structure in a B-Tree with Block Pointer and Data Pointer

A B-Tree node contains keys and pointers, pointers include child pointers (CP), a block pointer (BP), and data pointers (DP). Below is a detail of the node structure with these elements:

Let’s explain each component 

• BP (Block Pointer): It is Optional, used in disk-based storage which identifies the node’s location in storage (disk or memory). It does not point to other nodes; it only refers to the current node itself. In a disk-based B-Tree, every node is stored in a disk block, and the BP stores the disk address of that block. BP = 100 means this node is stored in disk block 100.

• Keys: it is stored in sorted order within the node and used for search and navigation.

• CP (Child Pointer): it points to child nodes (applicable for internal nodes) and used for tree traversal. CP1, CP2, CP3 … are child pointers pointing to disk blocks 200, 300, and 400 (child nodes).

• DP (Data Pointer): Points to the actual data records stored elsewhere. Each key is associated with a DP to access the corresponding data.

Example: Just like in a book, when you search for a topic (key), the B-Tree helps you jump directly to the relevant data block (BP) instead of scanning everything.

Insertion Rules (Block Pointer with Key Values)

Here are some rules that we must follow while insertion in the B tree

• The first child pointer (CP₀) points to the first child node, which contains values less than the first key (K₁).
• The second child pointer (CP₁) points to the second child node, which contains values greater than or equal to key (K₁) but less than key (K₂).
• The third child pointer (CP₂) points to the third child node, which contains values greater than or equal to key (K₂) but less than key (K₃).
• This pattern continues for all child pointers (CP) and keys (K).

B Tree Insertion at Leaf Level

B-tree, insertion always happens at the leaf level. Let’s go step by step to clarify the process:

1. Start at the Root

• Begin searching for the correct leaf node where the new key should be inserted.
• Traverse downwards by comparing the new key with the keys in the current node.

2. Finding the Correct Leaf Node

• If the new key is less than the first key in the node, follow the leftmost child pointer.
• Otherwise, continue comparing with other keys:
  • If the new key is greater than or equal to a key but less than the next key, move to the child pointer between those two keys.
  • If the key is greater than all existing keys, follow the rightmost child pointer.

3. Insertion at the Leaf

• Once the correct leaf node is found, insert the key at its correct position (in sorted order).
• If the leaf node has space (less than the maximum allowed keys), the insertion is complete.

4. Splitting the Node (If Needed)

• If the leaf node becomes full (exceeds the maximum number of keys), split it:
  • The middle key moves up to the parent node.
  • The left and right halves become separate nodes.
  • If the parent is also full, continue splitting up to the root.

This ensures that the B-tree remains balanced after every insertion.

Example 01: Insertion in B tree of Order 03

In this example, we will insert numbers 1,2,3,4,5,6,7, and 8 step by step.

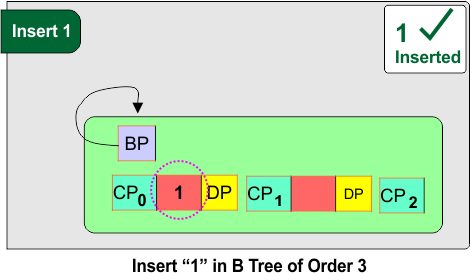
Step 01: Insert 1

Tree is empty, insert 1 as the first key.

Step 02: Insert 2

No overflow, insert 2 in sorted order.

 

Step 03: Insert 3 (Node Overflows – Splitting Required)

Node has 3 keys [1, 2, 3], overflows (exceeds order - 1 = 2 keys).

Split the node:

• The middle key 2 moves up as the root.
• Left child contains [1].
• Right child contains [3].

 

Very Important: In this example, CP₀ of key 2 and BP of key 1 will have the same value. CP₀ is used by the parent to point to the child, while BP in the child refers to itself

Step 04: Insert 4

4 > 2, go to the right child [3]. Insert 4 in sorted order.

Step 05: Insert 5 (Right Child Overflows – Splitting Required)

Step 01 Overflows

Right child [3, 4, 5] overflows.

Split:

• Middle key 4 moves up.
• Left child remains [3], the right child becomes [5].

Step 02: Block Pointer Rules Applied

• CP₀ → Points to [1] (values < 2). No problem
• CP₁ → Points to [3] (values ≥ 2 but < 4). No problem
• CP1 → Points to [5] (values ≥ 4). Problem found, its rule violation

Step 03: Resolve the issue 

• CP₀ → Points to [1] (values < 2). No problem
• CP₁ → Points to [3] (values ≥ 2 but < 4). No problem
• CP₂ → Points to [5] (values ≥ 4). No problem

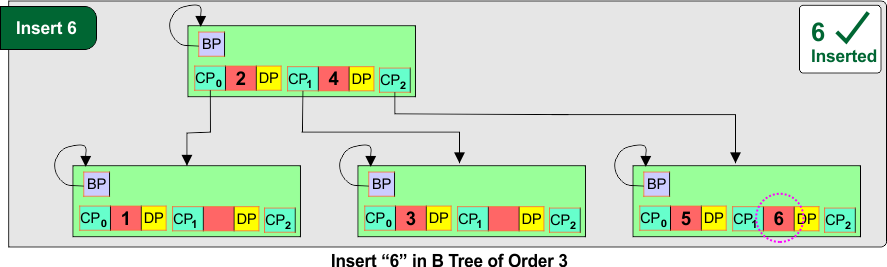
Step 06: Insert 6

6 > 4, go to the rightmost child [5]. Insert 6 in sorted order.

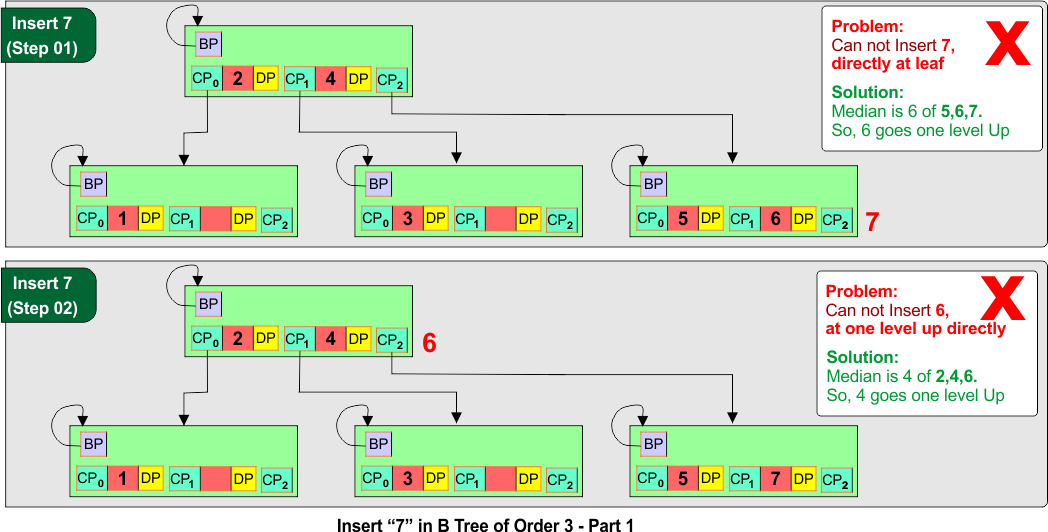
Step 07: Insert 7 (Right Child Overflows – Splitting Required)

Right child [5, 6, 7] overflows.

Split:

• Middle key 6 moves up.
• Left child remains [5], right child becomes [7].

Steps are similar as we insert 5 in step 05.

Step 08: Insert 8

8 > 6, go to the rightmost child [7]. Insert 8 in sorted order.

Example 02: Insertion in B Tree of Order 4

Following are the Properties of B-tree (Order 4)

• Each node can have at most 3 keys and 4 children.
• Each internal node (except the root) should have at least ceil(4/2) = 2 children.
• In case of overflow (more than 3 keys), split happens with a preference for left bias (placing more keys in the left child).

 

Step-by-step insertion into a B-tree of order 4

Let’s go step by step in inserting the numbers 5, 3, 21, 9, 1, 13, 2, 7, 10 into a B-tree of order 4 (Left Biased Tree).

Step 1: Insert 5

The tree is empty, so we start by inserting 5 as the root.\

Step 2: Insert 3

• Insert 3 into the same node and sort it.

Step 3: Insert 21

• Insert 21 and sort the keys.

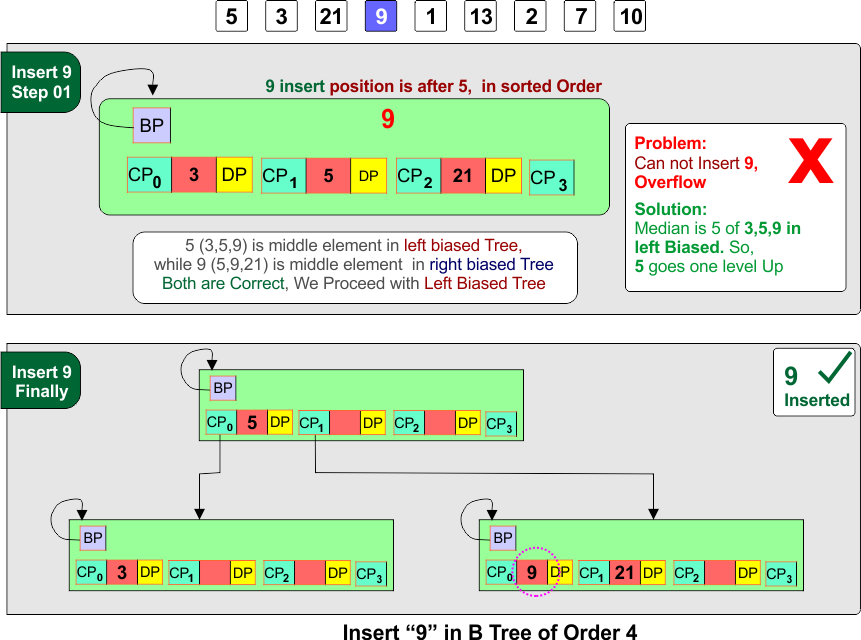
Step 4: Insert 9

• Insert 9 into the same node and sort the keys:
• The node now has 4 keys, which exceeds the limit of 3, so we split.
• Left-biased split:
  • 5 moves up to a new root.
  • Left child: [3]
  • Right child: [9, 21]

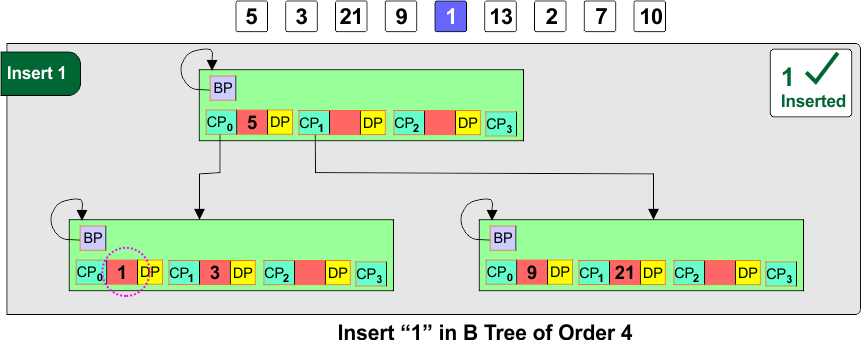
Step 5: Insert 1

• Insert 1 into the left child [3], keeping it sorted:

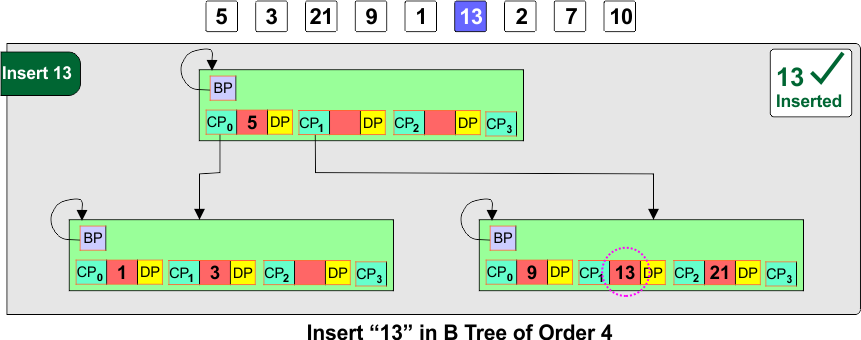
Step 6: Insert 13

• Insert 13 into the right child [9, 21], keeping it sorted:

Step 7: Insert 2

• Insert 2 into the left child [1, 3], keeping it sorted:

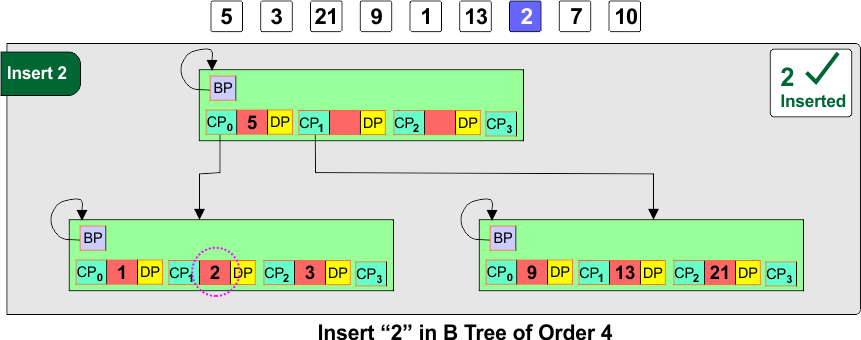
Step 8: Insert 7

• Insert 7 into the middle position. Since 7 belongs to the right child [9, 13, 21], insert it there and sort:

• The right child now has 4 keys, so it splits.
• Left-biased split:
  • 9 moves up to the root.
  • Left child: [7]
  • Right child: [13, 21]

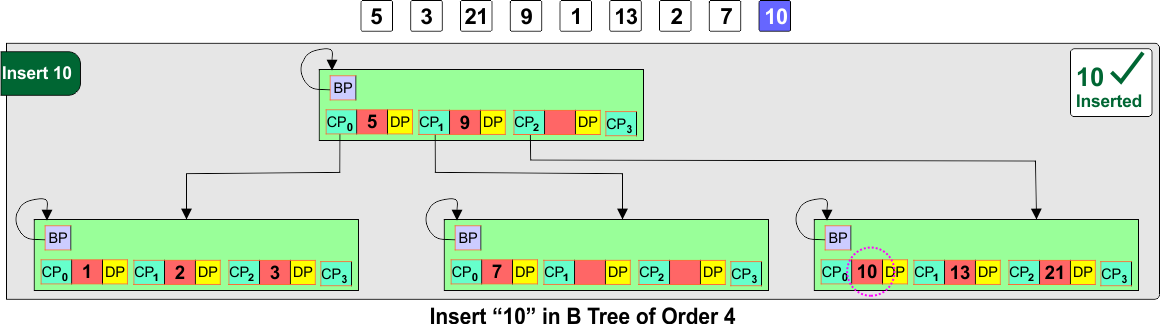
Step 9: Insert 10

• Insert 10 into the right child [13, 21], keeping it sorted