Heap Insert Time Complexity
Heap insertion uses the Heapify-Up process to maintain the heap property after adding a new element. There are two cases to see the time complexity of heap insertion
Case 01: Single Element Insertion (Heapify-Up)
This is the case when we already have a heap tree and we want to add one or more elements in it.
- Best Case: O(1) (If the new element is already in the correct position, no swaps are needed.)
- Worst Case: O(log N) (If the element moves from the last level to the root.)
Example: suppose we have 80,60,70,50,40,30,20 are different elements, and we want to insert new element 90 as in the following diagram
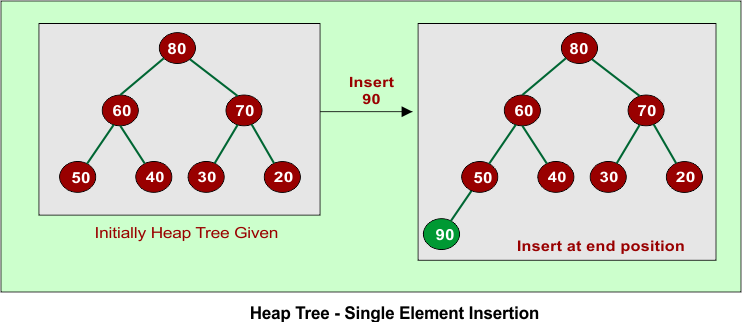
The time complexity calculations are given below

Bulk Insertion (Build Heap Using Heapify-Down)
This is the case when we do not already have a heap tree and want to add one or more elements to the heap tree.
- Best Case: O(N) (Heapify operations perform minimal swaps, mostly on the lower levels.)
- Worst Case: O(N) (Even in the worst case, Heapify-Down remains O(N), as most nodes require minimal swaps.)
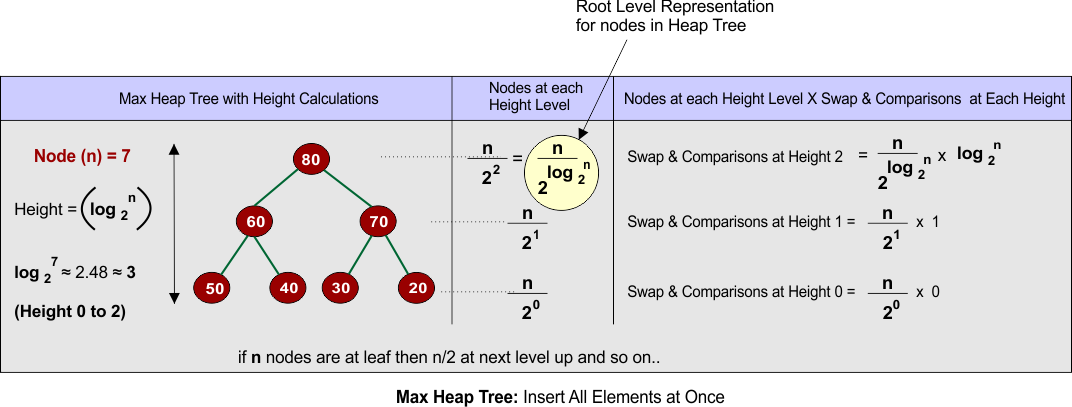

Summary Table of Time Complexity in Heap
| Method | Best Case | Worst Case |
|---|---|---|
| Insert 1 Element | O(1) | O(log N) |
| Insert N Elements One by One | O(N) | O(N log N) |
| Bulk Insert (Heapify-Down) | O(N) | O(N) |













