Basic Tree Terminologies In Data Structure

A tree is the most important part of the data structure to represent the hierarchical data. In this lecture, we will explain various basic tree terminologies in data structure.  These Terminologies include the following 

Let’s explain some of these in a single diagram.

Now let’s start with each terminology with a great explanation

1. Node

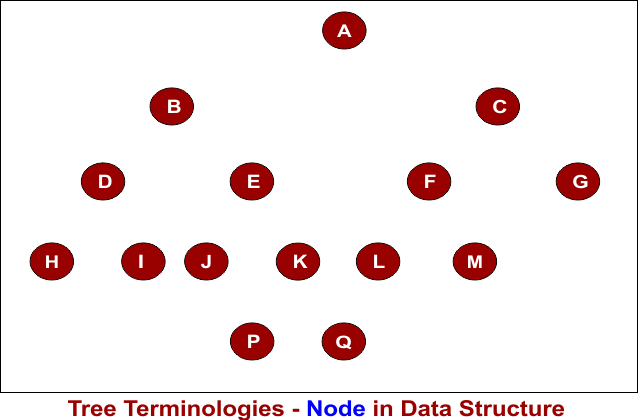
The node is the basic unit of the tree. A tree can hold several nodes that are connected to each other. In the following diagram, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, and P represent the different nodes.

2. Root

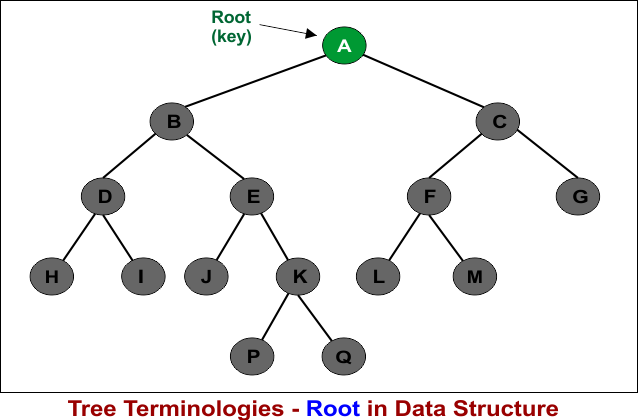
The root is the starting point of a tree. A tree can have only one root. More than one root node is not allowed. The root is also known as the key node. In the diagram above, node A is the root node.

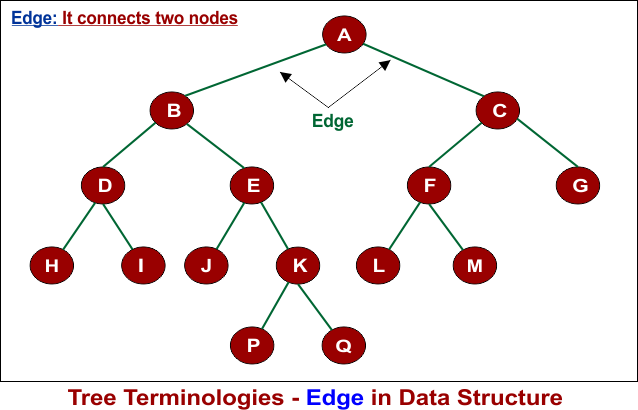
3. Edge

An edge, also referred to as a stick, connects two nodes. Without edges, we cannot connect the nodes. Therefore, edges are essential in a tree, as illustrated in the following diagram.

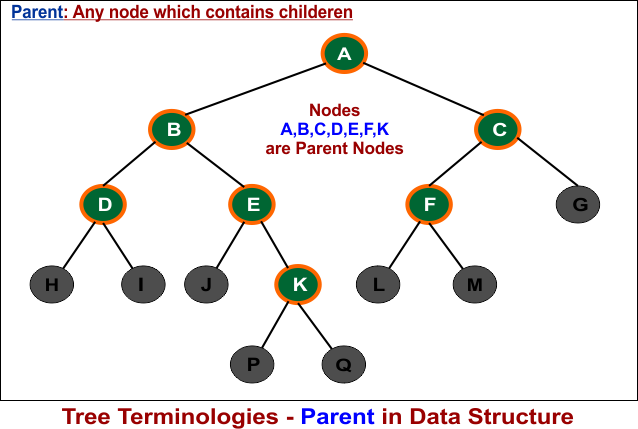
4. Parent 

Parent is a node which has one or more outgoing edges connecting to other nodes. Simply

• Any node in tree which containts childeren is called parent
• predecessor of any node is also called parent.

An internal (non leaf) node in a tree is any node that has at least one child. Internal nodes are located between the root and leaf nodes. The root node is considered an internal node if it has one or more children.

Important:

• The root node can be an internal node if it has children, but if the root is the only node in the tree, it is neither an internal node nor a leaf node. In this case, it is simply the root.
• parent nodes and internal nodes will always be the same because both types of nodes share the same characteristic: having children.

5. Child (Children)

A child node is a node that is immediately below a parent node in the tree. Simply, Any node which received a link/edge directly from its paraent is called its child. In tree, any parent node can hold any number of childern nodes. In tree all nodes are childern (or parent & childern at time) excep the root node.

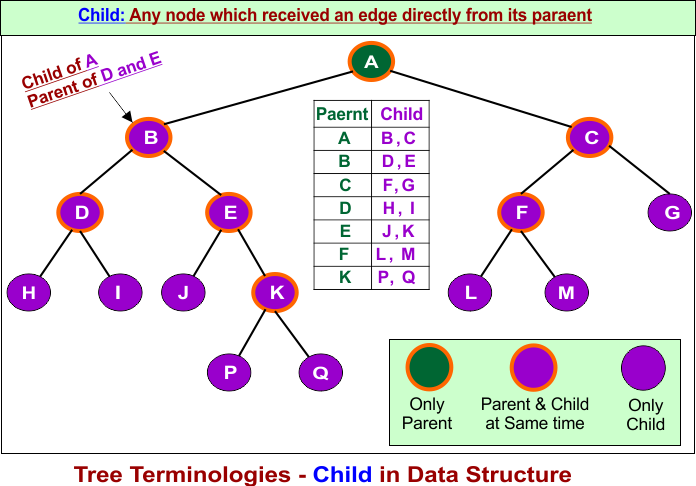
Important:  In above tree the Node D and E are not the direct children of A; because they are grandchildren (Descendant ) of A, As D and E are connect through B with A. So, Children are descendants but only the direct ones. 

6. Descendant

A parent node contains both children and descendants but they are different. Descendants are all the nodes on the path from a specific node to the leaf nodes, excluding the specific node itself but including all its children, grandchildren, great-grandchildren, and so on.). Its direction is from the root node to the leaf node. All nodes are descendant except the root node. The descendants of each node are given below

Leaf nodes have no descendants because no nodes below them. As In the above diagram H, I, J, P, Q, L, M, and G contain no descendant. All Children are descendants but not vice versa.

7. Ancestors

Ancestors are all the nodes on the branch path from a specific node (typically a leaf or any node) to the root node, including the root itself but excluding the specific node. It direction is opposite to the descendant where

• Descendants move downward from a node (towards the leaf nodes).
• Ancestors move upward from a node (towards the root).

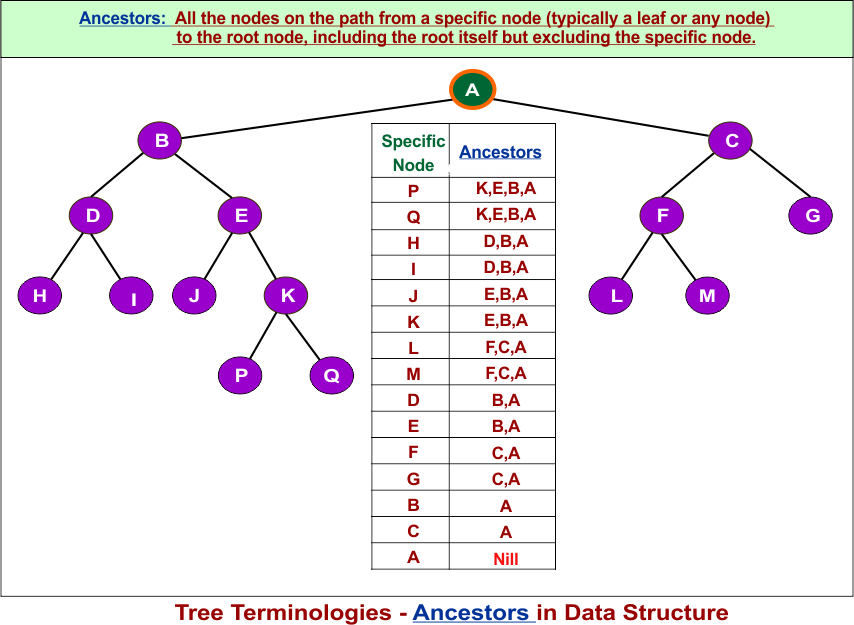
The root node has no ancestors.

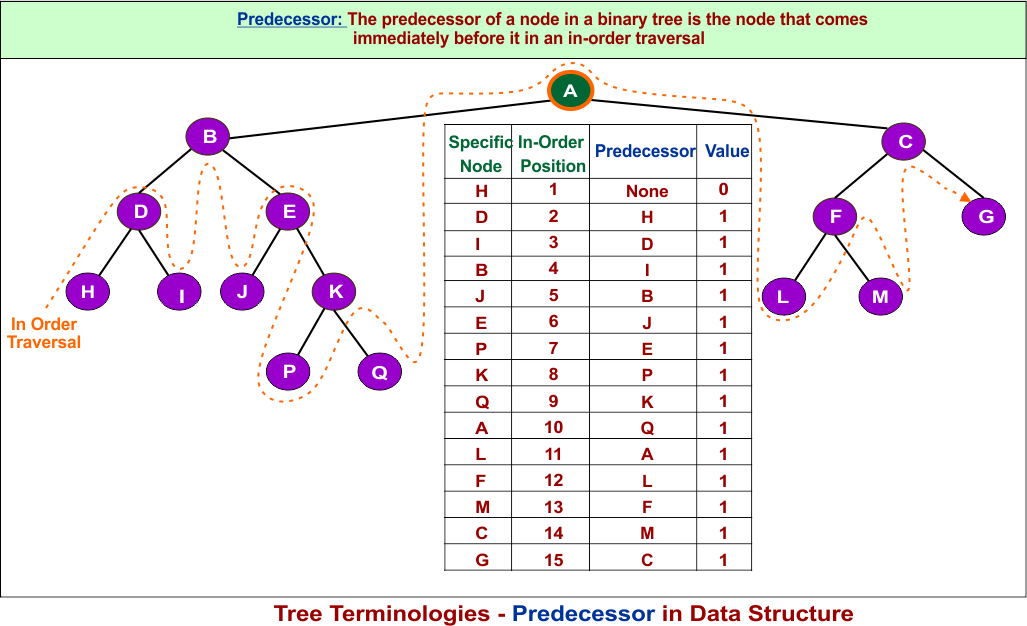
8. Predecessor

Before learning about the predecessor, you must know about in-order traversal of tree.

The predecessor of a node in a binary tree is the node that comes immediately before it in an in-order traversal. Predecessor value can be 0, 1 only.

• Predecessor Value = 0: Occurs when a node does not have a predecessor in the in-order traversal.
• Predecessor Value = 1: Occurs when a node has exactly one predecessor, which is the node appearing immediately before it in the in-order traversal.

In-Order Traversal: H, D, I, B, J, E, P, K, Q, A, L, F, M, C, G

9. Successor

A successor is the immediate next node in the in-order traversal. For example:

• The successor of H: D (the node after H in the traversal).
• Successor of E: P (the node after E in the traversal).
• The successor of G: None (G is the last node in the traversal).

Successor Value = 0: Occurs when a node does not have a successor in the in-order traversal (i.e., it is the last node in the traversal).

Successor Value = 1: Occurs when a node has exactly one successor, which is the node appearing immediately after it in the in-order traversal.

In-Order Traversal: H, D, I, B, J, E, P, K, Q, A, L, F, M, C, G

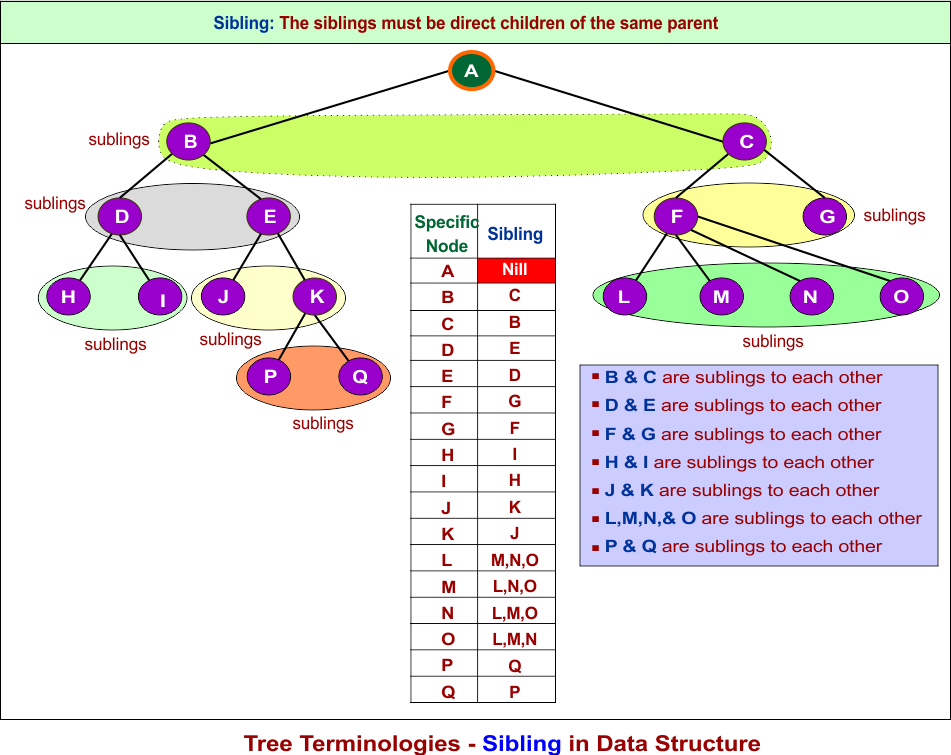
10. Siblings

Siblings are nodes that have the same parent. siblings must be direct children of the same parent, and all children of a parent exist at the same level.  It is not possible for siblings to share the same parent but exist at different levels because the tree structure does not allow it.

Important: Root node cannot have any siblings because it has no parent.

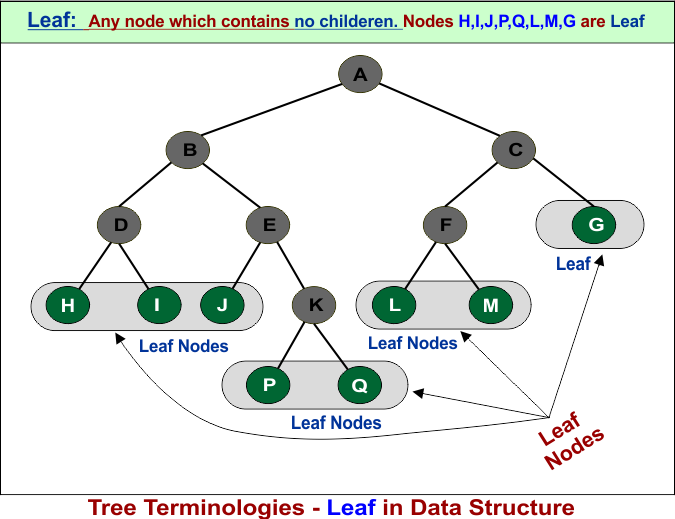
11. Leaf Node (External Nodes)

A leaf node is a node in a tree data structure that has no children. In other words, it does not have any outgoing edges. It is the endpoint of a branch. Alternate names for leaf node are Terminal or External node.

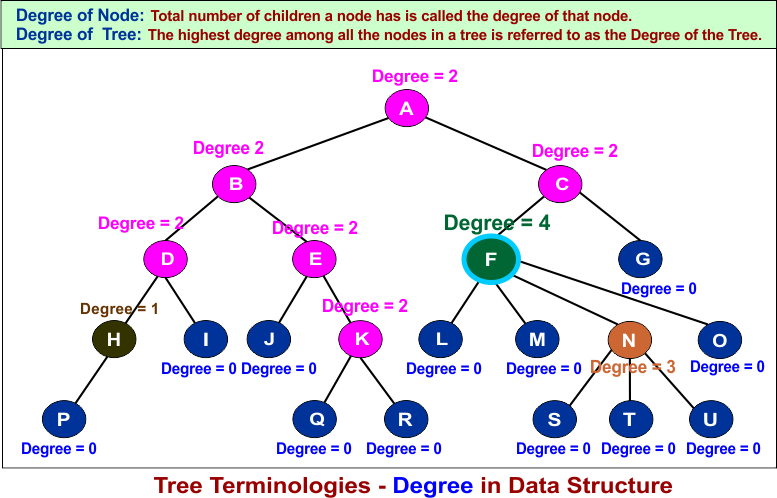
12. Degree

In a tree data structure, the total number of children a node has is called the degree of that node. The highest degree among all the nodes in a tree is referred to as the Degree of the Tree.

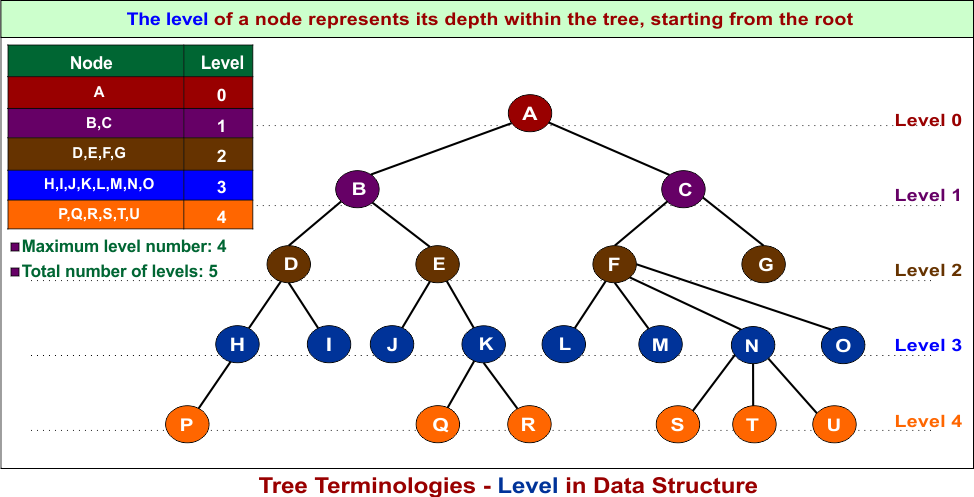
13. Level and Depth

• The level of a node represents its depth within the tree, starting from the root. The root is at level 0, its children are at level 1, and so on.
• The depth of a node is the number of edges on the path from the root to that node.

Depth and Level are the same concepts with the same numeric value. but one key difference

Depth always starts at 0 for the root node. But the level can at 0 or 1 for the root node.

• Numerically Same: If levels start from 0, level = depth.
• Numerically Different: If levels start from 1, level = depth + 1.

The maximum value of Level is the Level of that tree, in the above diagram, the level of the tree is 5 (0 to 4).

In most practical contexts, level and depth are interchangeable because their numeric values are the same. The difference lies in their interpretation or context. Conceptually, level describes the “layer” of the tree, often used in breadth-first traversal. Depth is used more technically in algorithms, especially when analyzing recursion or paths.

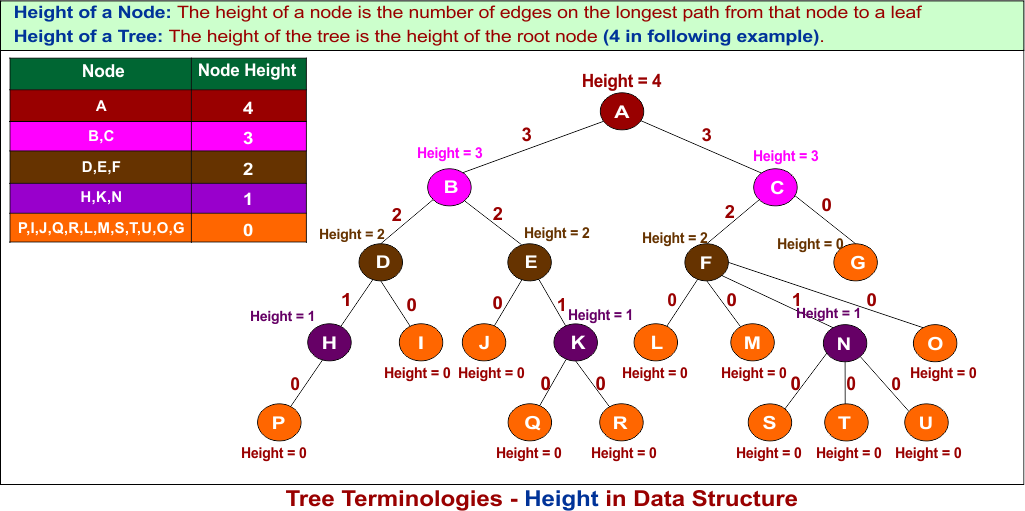
14. Height

Height of a Node: The height of a node is the number of edges on the longest path from that node to a leaf.

Height of a Tree: The height of the tree is the height of the root node.

• If the tree is empty, the height is -1.
• If the tree has only one node (the root), the height is 0.
• Otherwise, the height is the maximum depth of all leaf nodes.

15. Subtree

A subtree of a tree is a portion of the tree that itself satisfies the properties of a tree. A subtree consists of a node (called the root of the subtree) and all its descendants.

Rules for a Subtree

1. A subtree is itself a tree, meaning:
   • It must have a single root.
   • There are no cycles.
   • Every child of a node belongs to the subtree of its parent.
2. Any node in the tree can act as the root of a subtree.
3. The entire tree is also considered a subtree of itself.

Subtree Examples

Key Points

1. Leaf Nodes: Each leaf node is considered a subtree of itself. For example, B, D, G, and H are subtrees in the example.
2. Root Node: The whole tree rooted at A is a subtree.
3. Subtree Size: The size of a subtree is the total number of nodes in it.

16. Path

In a tree, there is exactly one unique path between any pair of nodes because trees are connected and acyclic (no cycle). We can explain the concept of path through three different scenarios

1. Paths Between Nodes pair

In a tree, there is exactly one unique path between any pair of nodes because trees are connected and acyclic.

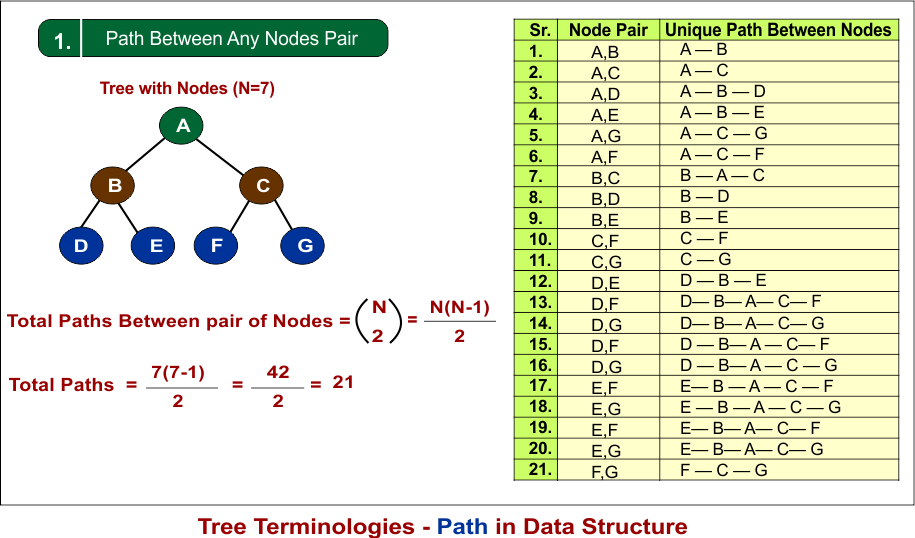
The above diagram shows 21 unique paths between all pairs of nodes.

2. Root-to-Leaf Paths

The number of root-to-leaf paths equals the number of leaf nodes, as each leaf node can only be reached by one unique path from the root.

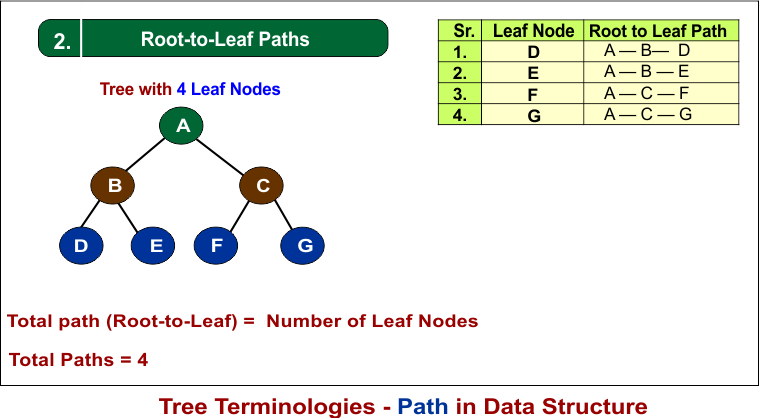
The above diagram shows 4 root-to-leaf paths.

3. Subtree Paths

A subtree path includes all possible paths within a subtree

Summary

• Total Paths Between Nodes: 21 (all pairs of nodes).
• Root-to-Leaf Paths: 4 (based on 4 leaf nodes).
• Subtree Paths: 44 (all possible paths within all subtrees).

17. Branch

A branch in a tree is a subtree that starts from a given node and includes all its descendants. When all nodes are considered,

Total number of branches = Total number of nodes.

All branches are subtrees, but not all paths are branches because paths do not necessarily include all descendants. Every branch contains multiple paths, but not every path can be considered a branch. Path and Branch concepts are almost the same but here are some key differences.

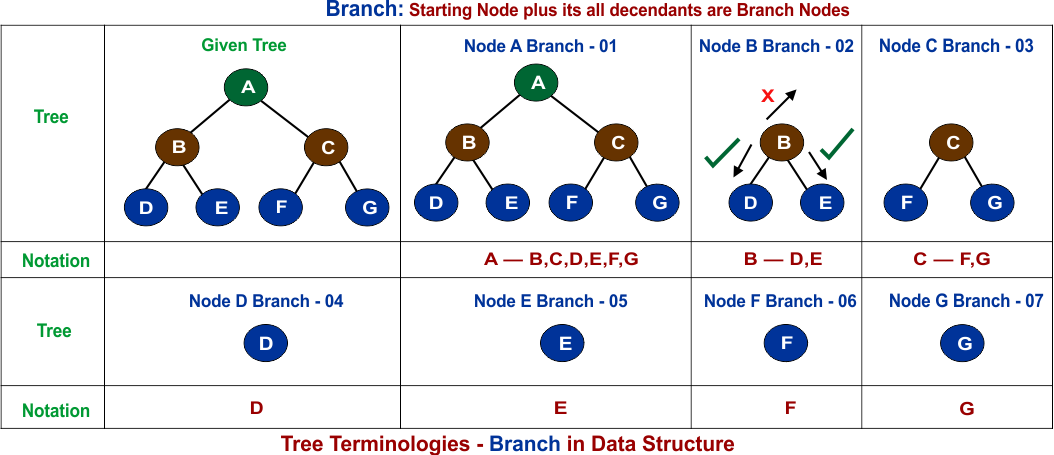
Path:

• A path must have at least 2 nodes because it represents a connection.
• Can go upwards (towards the root) or downwards (towards the leaves).
• Has a length, defined as the number of edges between nodes.

Branch:

• A branch can have just 1 node (e.g., a leaf node is its own branch).
• Always goes downwards, starting from a node and extending to all its descendants.
• Has a height (longest path from the starting node to a leaf).

Example 01: Upward and downward movement in Path and branch

The path from $G$ to $E$: $G-C-A-B-E$

• It starts at G, goes up to $C$, up to $A$, then down to $B$, and ends at $E$. Branches always include the starting node and all descendants (it represents a subtree).

Branch starting at C: (Includes C and all its descendants $F$ and $G$.)

Example: 02: Path and Branch at same node (“B”)

• The branch starting at B includes B itself, and it descendants D, and E. which also contains paths like B−D, B−E, and B−D−E.
• The Path starting at Node B includes the following possible path.
  • B – D
  • B – E
  • B – A
  • B – A – C
  • B – A – C – F
  • B – A – C – G