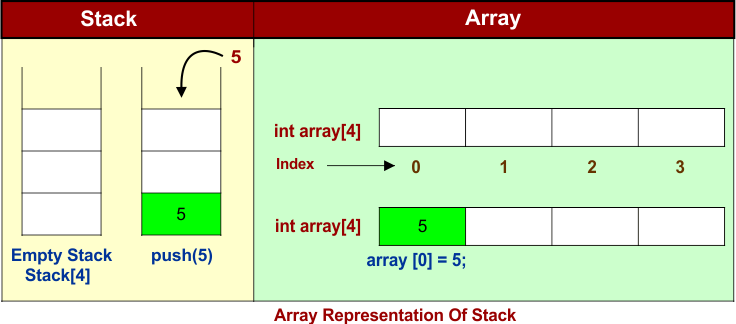
Array Representation Of Stack
A stack is a data structure that can be implemented using arrays or linked lists, this article focuses on array representation of a stack, its advantages, implementation, and practical usage.
- Array: An array is a linear data structure that stores a collection of elements in contiguous memory locations. Each element in the array can be accessed directly using its index. Arrays are ideal for situations where elements need to be stored and accessed sequentially.
- Stack: A stack is a linear data structure that follows the Last In, First Out (LIFO) principle. This means that the last element added to the stack is the first one to be removed. Stacks are commonly implemented using arrays or linked lists and are used for tasks such as expression evaluation, backtracking, and function call management.
Key Similarities Between Array and Stack
Here’s a summary of the key similarities between arrays and stacks:
| Aspect | Array | Stack |
|---|---|---|
| Linear Structure | Both are linear data structures, meaning elements are stored sequentially. | A stack is a linear data structure, but elements follow the LIFO (Last In, First Out) order. |
| Fixed Size | If statically declared, arrays have a fixed size (e.g., int arr[10]). |
Stack size is fixed if implemented using an array. |
| Index-Based Access | Elements in an array are accessed via index, starting from 0. | In an array-based stack, the index tracks the position of the top element. |
| Memory Allocation | Requires contiguous memory for storage. | It uses contiguous memory if implemented with an array. |
Key Difference Between Array and Stack
| Key Feature | Array | Stack |
|---|---|---|
| Access | Access any element directly using its index. | Access only the top element (LIFO). |
| Insertion/Removal Order | Insert/remove at any position using index. | Insert (push) and remove (pop) only at the top. |
| Data Type | Stores multiple elements of the same data type (e.g., all integers). | It can store different data types if implemented with generic pointers (void*). It is called “generic” because it can point to any data type |
In the array-based implementation, a stack is represented using an array and a variable (usually called top) to track the index of the topmost element. This approach is simple and efficient for applications where the maximum size of the stack is known in advance.
Key Advantages of Array Representation Of Stack
when we implement the stack using array or linked list it take order of consent in term of time and space for the following specific operations which make it more efficient.
| Operation | Description | Time Complexity | Space Complexity |
|---|---|---|---|
| isEmpty | Checks if the stack is empty. Returns true if empty, false otherwise. | O(1) | O(1) |
| Push | Adds an element to the top of the stack. | O(1) | O(1) |
| Pop | Removes the top element from the stack. | O(1) | O(1) |
| Peek | Returns the top element without removing it. | O(1) | O(1) |
Stack Operations Using Array
Let’s explore a C implementation of stack operations and discuss the key functions.
1. Push Operation: Adding Elements to the Stack
The push operation adds an element to the top of the stack. However, before performing a push, it’s crucial to check if the stack is full. Here’s how it’s done in C:
| void push(int value) { if (isFull()) { printf(“Stack is full! Cannot push %d\n”, value); } else { stack[++top] = value; printf(“%d pushed onto stack\n”, value); } } |
2. Pop Operation: Removing Elements from the Stack
The pop operation removes the top element from the stack. If the stack is empty, it returns an error message.
| int pop() { if (isEmpty()) { printf(“Stack is empty! Cannot pop\n”); return -1; } else { return stack[top–]; } } |
The isEmpty function checks whether the stack is empty (i.e., top == -1). If so, the pop operation cannot proceed. Otherwise, the top element is removed, and the top index is decremented.
3. Peek Operation: Viewing the Top Element
The peek operation lets you view the top element of the stack without removing it. This is useful for checking the current state of the stack.
| int peek() { if (isEmpty()) { printf(“Stack is empty! Cannot peek\n”); return -1; } else { return stack[top]; } } |
The function checks if the stack is empty before accessing the top element, ensuring no invalid access occurs.
4. Size and Count Operations
Understanding the size and the current number of elements in a stack is important. The size function returns the maximum capacity of the stack, while the count function tells you how many elements are currently in the stack.
| int size() { return MAX; }int count() { return top + 1; } |
- size returns the maximum stack size (
MAX), which is set to 5 in this example. - count calculates the number of elements in the stack by returning
top + 1, sincetoprepresents the index of the last element.
5. Change Operation: Modifying an Element in the Stack
You can modify an element at a specific position in the stack using the change function. This is helpful when you need to update an element without removing it.
| void change(int position, int value) { if (position < 0 || position > top) { printf(“Invalid position!\n”); } else { stack[position] = value; printf(“Element at position %d updated to %d\n”, position, value); } } |
This function checks if the position is valid (i.e., it’s within the current stack size) before making the change.
6. Display Operation: Showing All Stack Elements
Displaying the elements in the stack allows users to inspect its current state.
| void display() { if (isEmpty()) { printf(“Stack is empty!\n”); } else { printf(“Stack elements: “); for (int i = 0; i <= top; i++) { printf(“%d “, stack[i]); } printf(“\n”); } } |
If the stack is empty, the display function prints an empty message. Otherwise, it prints all elements currently in the stack from the bottom to the top.
Simple C Program: Stack Using Array
| #include <stdio.h> #include <stdlib.h>#define MAX 5 // Maximum size of the stackint stack[MAX]; int top = -1; // Initialize top of stack// Function to check if the stack is full int isFull() { return top == MAX – 1; }// Function to check if the stack is empty int isEmpty() { return top == -1; }// Function to push an element onto the stack void push(int value) { if (isFull()) { printf(“Stack is full! Cannot push %d\n”, value); } else { stack[++top] = value; printf(“%d pushed onto stack\n”, value); } } // Function to pop an element from the stack // Function to peek the top element of the stack // Function to return the size of the stack // Function to count the total number of elements in the stack // Function to change an element at a specific position in the stack // Function to display all elements in the stack int main() { printf(“Top element is %d\n”, peek()); printf(“%d popped from stack\n”, pop()); change(0, 100); // Update the element at position 0 printf(“Stack size is %d\n”, size()); if (isEmpty()) { return 0; |
Output:
5 pushed onto stack 10 pushed onto stack 40 pushed onto stack Top element is 40 40 popped from stack 10 popped from stack Element at position 0 updated to 100 Stack elements: 100 Stack size is 5 Number of elements in the stack: 1
Advance C program: Stack Using Array
The key point in this code is, it take all input from the user
#include <stdio.h>
#include <stdlib.h>
int *stack; // Dynamic stack
int top = -1; // Initialize top of stack
int maxSize;
// Function to check if the stack is full
int isFull() {
return top == maxSize – 1;
}
// Function to check if the stack is empty
int isEmpty() {
return top == -1;
}
// Function to push an element onto the stack
void push(int value) {
if (isFull()) {
printf(“Stack is full! Cannot push %d\n”, value);
} else {
stack[++top] = value;
printf(“%d pushed onto stack\n”, value);
}
}
// Function to pop an element from the stack
int pop() {
if (isEmpty()) {
printf(“Stack is empty! Cannot pop\n”);
return -1; // Return a value to indicate failure
} else {
return stack[top–];
}
}
// Function to peek the top element of the stack
int peek() {
if (isEmpty()) {
printf(“Stack is empty! Cannot peek\n”);
return -1;
} else {
return stack[top];
}
}
// Function to count the total number of elements in the stack
int count() {
return top + 1;
}
// Function to change an element at a specific position in the stack
void change(int position, int value) {
if (position < 0 || position > top) {
printf(“Invalid position!\n”);
} else {
stack[position] = value;
printf(“Element at position %d updated to %d\n”, position, value);
}
}
// Function to display all elements in the stack
void display() {
if (isEmpty()) {
printf(“Stack is empty!\n”);
} else {
printf(“Stack elements: “);
for (int i = 0; i <= top; i++) {
printf(“%d “, stack[i]);
}
printf(“\n”);
}
}
int main() {
// Ask user for the size of the stack
printf(“Enter the size of the stack: “);
scanf(“%d”, &maxSize);
// Dynamically allocate memory for the stack based on user input
stack = (int *)malloc(maxSize * sizeof(int));
int choice, value, position;
do {
printf(“\nStack Operations:\n”);
printf(“1. Push an element onto the stack\n”);
printf(“2. Pop an element from the stack\n”);
printf(“3. Peek the top element\n”);
printf(“4. Change an element at a specific position\n”);
printf(“5. Display all elements\n”);
printf(“6. Exit\n”);
printf(“Enter your choice: “);
scanf(“%d”, &choice);
switch (choice) {
case 1:
// Push operation
printf(“Enter the value to push: “);
scanf(“%d”, &value);
push(value);
break;
case 2:
// Pop operation
value = pop();
if (value != -1) {
printf(“%d popped from stack\n”, value);
}
break;
case 3:
// Peek operation
value = peek();
if (value != -1) {
printf(“Top element is %d\n”, value);
}
break;
case 4:
// Change operation
printf(“Enter the position to change (0 to %d): “, top);
scanf(“%d”, &position);
printf(“Enter the new value: “);
scanf(“%d”, &value);
change(position, value);
break;
case 5:
// Display operation
display();
break;
case 6:
printf(“Exiting program…\n”);
break;
default:
printf(“Invalid choice! Please try again.\n”);
}
} while (choice != 6);
// Free allocated memory
free(stack);
return 0;
}
Output:
Enter the size of the stack: 15 Stack Operations: 1. Push an element onto the stack 2. Pop an element from the stack 3. Peek the top element 4. Change an element at a specific position 5. Display all elements 6. Exit Enter your choice: 1 Enter the value to push: 20 20 pushed onto stack Stack Operations: 1. Push an element onto the stack 2. Pop an element from the stack 3. Peek the top element 4. Change an element at a specific position 5. Display all elements 6. Exit Enter your choice:
Implementation of Multiple Stack using Array
Implementing multiple stacks using an array can be done in two common ways: fixed partitioning (where the array is divided into equal sections for each stack) and dynamic partitioning (where stacks grow toward each other, making more efficient use of available space). Below, I'll show how to implement multiple stacks using a single array with both approaches.
1. Fixed Partitioning Approach
In this method, we divide the array into fixed parts for each stack. For example, if we have an array of size N and want k stacks, each stack gets an equal portion of the array.

2. Dynamic Partitioning Approach
In dynamic partitioning, the stacks grow toward each other, meaning one stack grows from the left side of the array, and another grows from the right side. This is more flexible as stacks can expand based on the available space.

Important: no more items can be pushed into a stack when both top items are adjacent to each other













