Heap Sort with Example – Time Complexity
Heap Sort is a comparison-based sorting algorithm that converts an array into a heap data structure and repeatedly extracts the largest (or smallest) element to sort the array.
- It uses a heap data structure
- Efficient for large datasets
- Not stable (does not maintain the relative order of equal elements)
- In-place sorting (does not require extra memory)
Heap Sort consists of two steps, The Heap Sort Working Mechanism is given below
Step 01: Build Heap
This converts the array into a Max Heap (or Min Heap for ascending order).

Step 02: Delete Elements and Heapify
Repeatedly removes the maximum element (root), swaps it with the last element, and re-heapifies to maintain the heap property. Follwoing diagrams explain the concept in more detail.
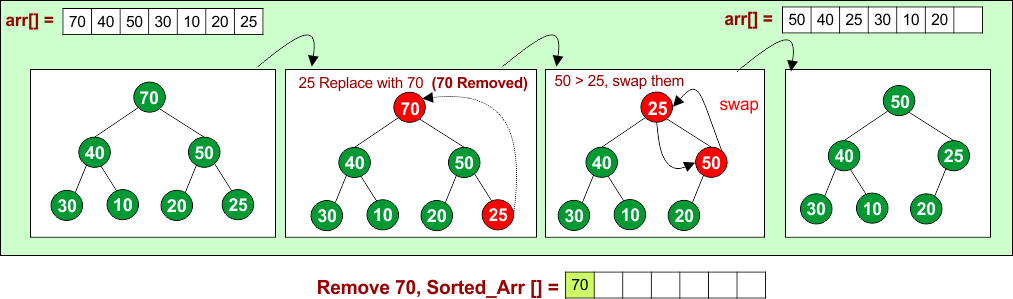
Remove 70:
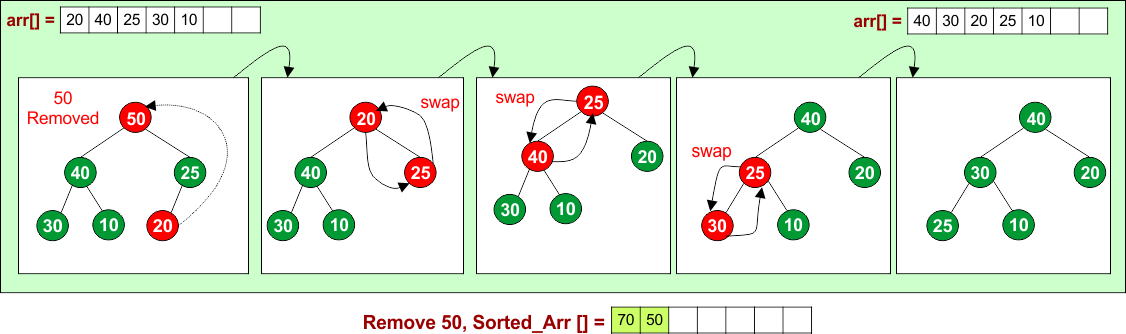
Remove 50:
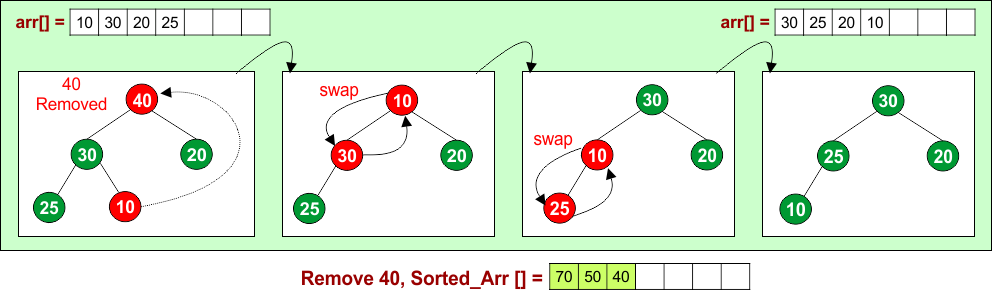
Remove 40:
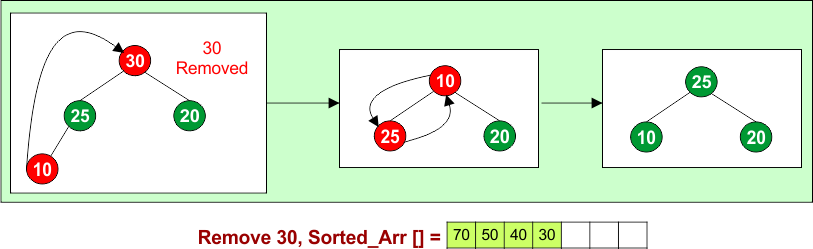
Remove 30:
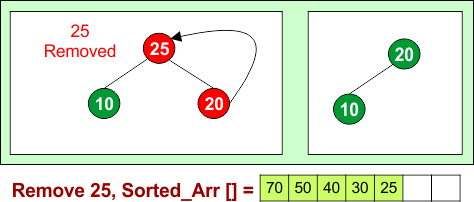
Remove 25:
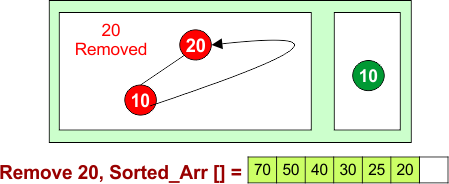
Remove 20:
Remove 10:
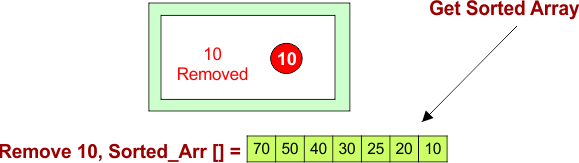
Finally, we get sorted Array, after completing two steps
Time Complexity Calculation
Heap Sort has a consistent time complexity of O(n log n) in best and worst case. Calculations are given in the following table.
| Step | Complexity |
|---|---|
| Building Heap | O(n) |
| Delete Root & Heapify | O(n log n) |
| Total Complexity | O(n + n log n) = O(n log n) |













