Types of Trees In Data Structure

Trees are a fundamental non-linear data structure widely used in computer science. They offer efficient methods for storing, managing, and retrieving hierarchical data, making them essential in databases, file systems, artificial intelligence, and more. Understanding the various types of trees in data structures helps to solve complex problems like searching, sorting, and indexing with improved performance.

In this article, we’ll explore different types of trees, including binary trees, binary search trees (BST), AVL trees, B-trees, and others, along with their applications and key properties.

Types of Trees based on the number of children in Data Structure

Trees can be categorized in data structures based on the number of children a node can have. Here are the main types:

1. General Tree

A tree in which a node can have any number of children.

2. Binary Tree

A tree where each node can have at most two children (left and right).

3. Ternary Tree

A tree where each node can have at most three children.

4. N-ary Tree

A generalized tree where each node can have at most N children.

For Example: N = 5 

Each node can have at most 5 children.

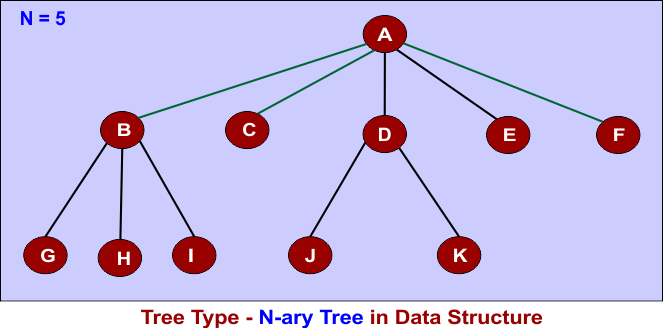
It is used in Trie (prefix trees), B-Trees (databases), and XML parsing.

A binary tree is a tree where each node has at most two children (left and right). Binary trees can be classified into several types based on structure and properties.

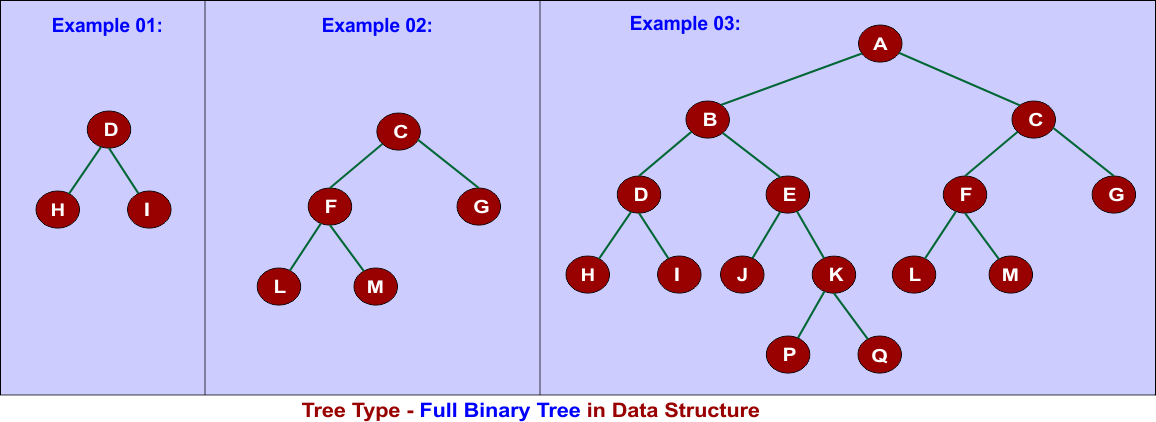
5. Full Binary Tree (Strict Binary Tree)

In a full binary tree, every node has either two or no children. This structure is also referred to as a proper binary tree.

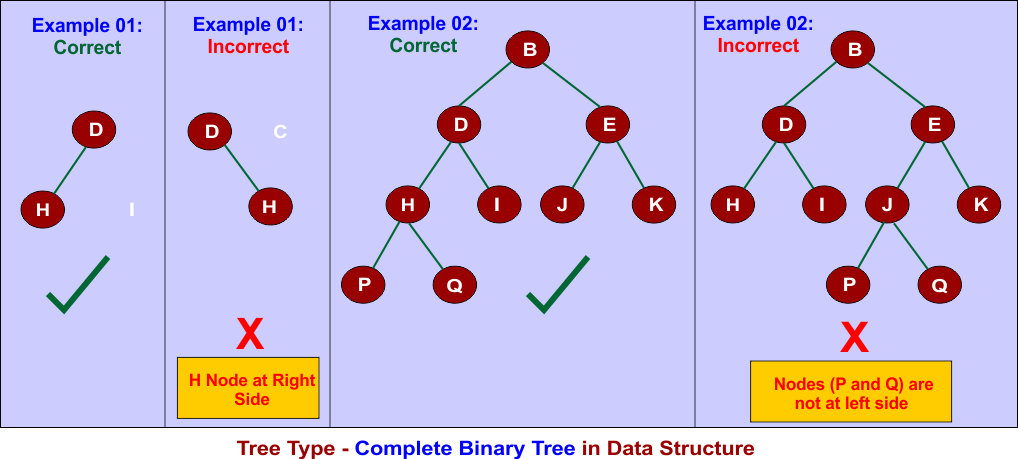
6. Complete Binary Tree

All levels are completely filled except the last, which is filled from left to right.

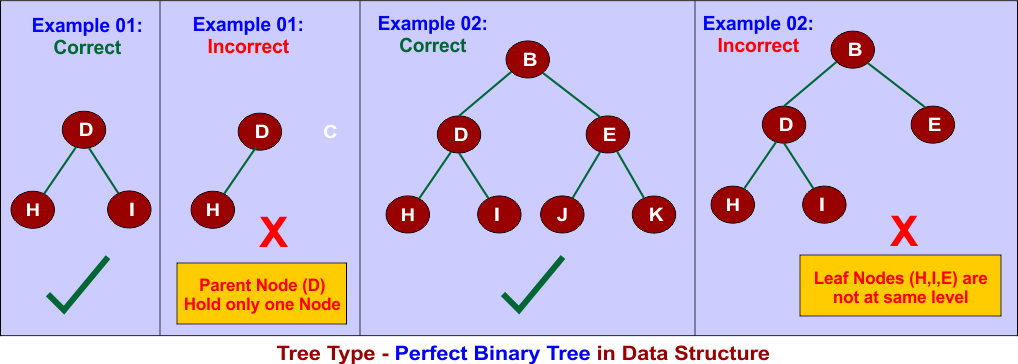
7. Perfect Binary Tree

A binary tree where all leaf nodes are at the same level, and all parent nodes have two children.

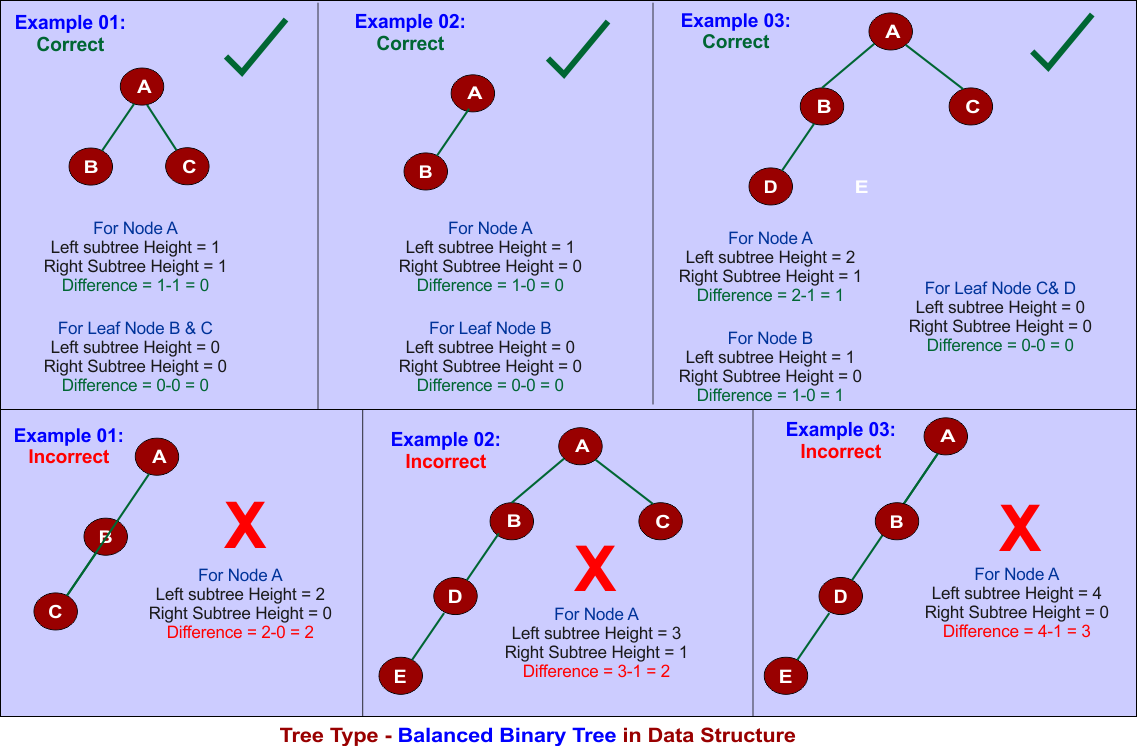
8. Balanced Binary Tree

A Balanced Binary Tree is a tree where, for every node, the height of the left subtree and the height of the right subtree differs by -1, 0, or 1  (no more than 1)

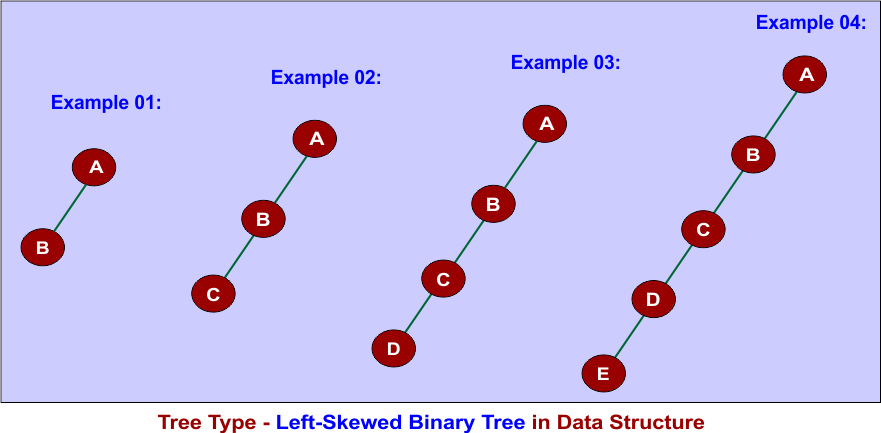
9. Degenerate Binary Tree (Left-Skewed)

Each node has a single left child. The height of the tree equals the number of nodes (n).

10. Degenerate Binary Tree (Right-Skewed)

Each node has only one right child. The height of the tree is equal to the number of nodes (n).

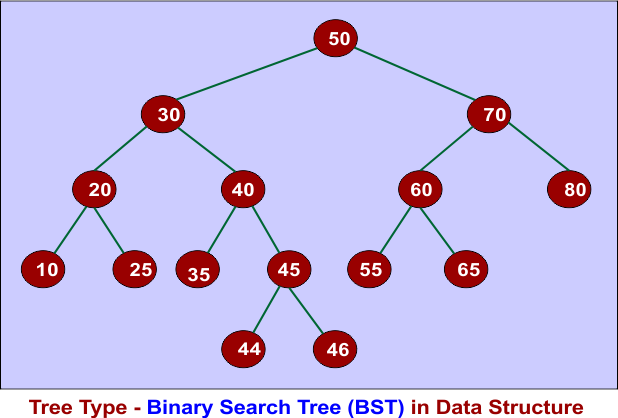
11. Binary Search Tree (BST)

It is a special type of binary tree where:

• Each node has at most two children.
• Left subtree contains values smaller than the node.
• Right subtree contains values greater than the node.
• No duplicate values (in a strict BST).

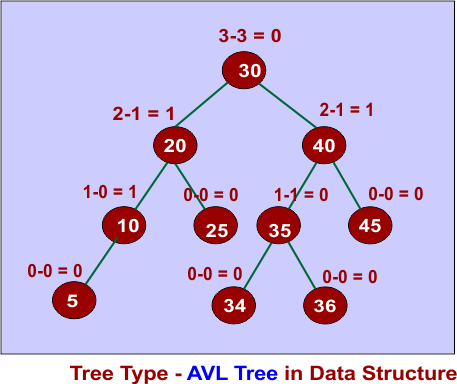
12. AVL Tree

AVL tree must hold the following

• Binary Search Tree (BST) Property
  • The left subtree contains values less than the node.
  • The right subtree contains values greater than the node.
• Balance Factor
  • Balance Factor = Height of Left Subtree – Height of Right Subtree
  • Valid AVL Tree: Balance Factor ∈ {-1, 0, 1}
• Self-Balancing
  • After insertion or deletion, if the balance factor violates {-1, 0, 1}, rotations are performed to restore balance.

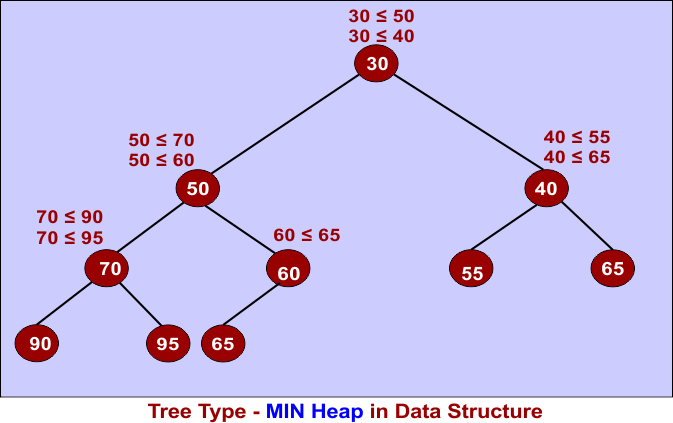
13. Heap Trees

A Heap is always a Complete Binary Tree (CBT). This means that all levels are completely filled, except possibly the last level, which is filled from left to right. The heap is of two types

1.) Min Heap: Parent nodes are smaller than or equal to their children.

2). Max Heap: Parent nodes are greater than or equal to their children.

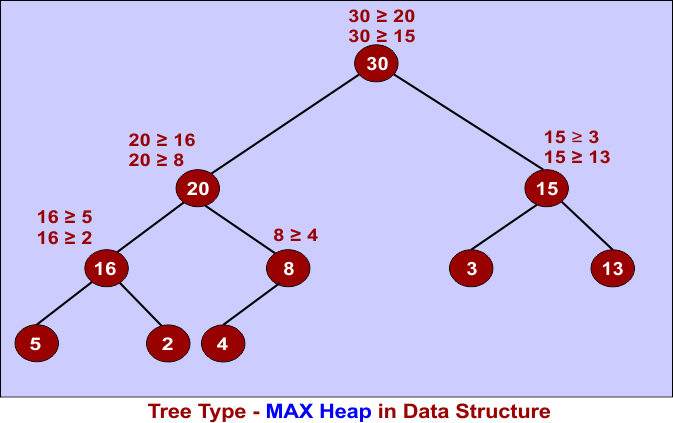
It is used in priority queues and heap sort.

14. Red-Black Tree (RBT) Definition

A Red-Black Tree is a self-balancing binary search tree (BST) that ensures the tree remains balanced by following specific rules. This balance helps maintain an efficient search, insertion, and deletion time of O(log n).

Properties of a Red-Black Tree

1. Each node is either red or black.
2. The root node is always black.
3. No two consecutive red nodes appear (no red-red parent-child).
4. Every path from a node to its NULL (leaf) descendants has the same number of black nodes.
5. Newly inserted nodes are always red.

These properties help maintain the balanced structure of the tree.

Example of a Red-Black Tree

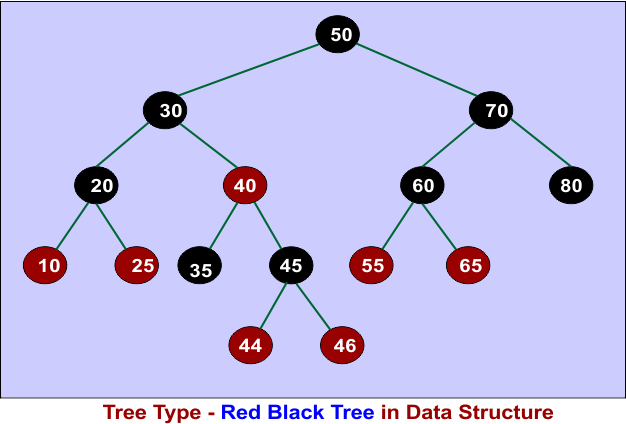
• The tree follows BST order (left subtree < root < right subtree).
• No two red nodes are adjacent.
• Each path from root to leaf has the same number of black nodes.

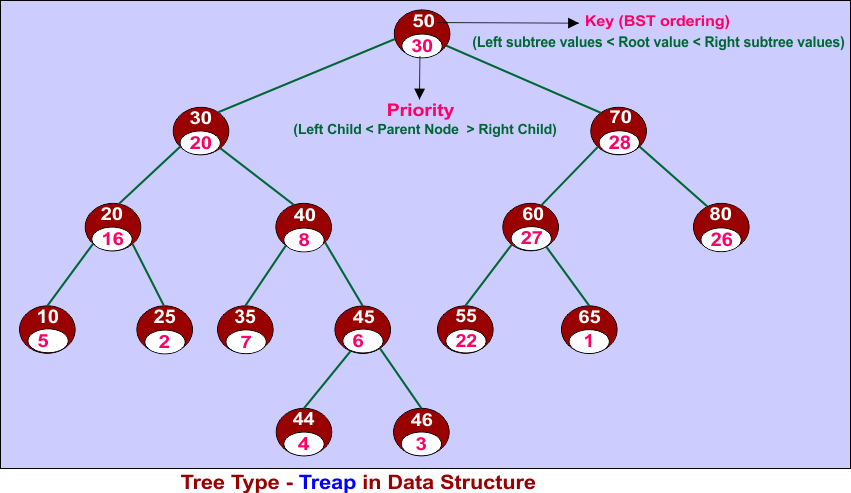
15. Treap (Tree + Heap)

A Treap is a self-balancing binary search tree (BST) that combines properties of a BST and a Heap to maintain balance.

Properties of a Treap

1. Follows BST Order:
   • Left subtree values < Root value < Right subtree values.
2. Follows Max Heap Order on Priorities:
   • Each node has a random priority.
   • The parent’s priority is greater than both children’s (Max-Heap).
3. Self-Balancing Using Rotations:
   • If heap property is violated, rotations (like in AVL Trees) restore balance.

Example: Each node in a Treap holds two values:

1. Key – follows the standard BST ordering (the left is smaller and the right is greater).
2. Priority – a randomly assigned value that complies with the Max-Heap property.