Infix expressions, like A + B, have operators between operands, making them easy for humans to understand but challenging for machines to evaluate. Postfix notation eliminates the need for parentheses by placing operators after their operands, simplifying computation. In this class we will see how to convert infix to postfix with various examples.

Rules for Infix to Postfix Conversion

• Operands: Directly append operands (like A, B, or 1) to the output.
• Operators: Use a stack to manage operators based on their precedence and associativity.
  • Precedence: ^ (highest), * and / (medium), + and - (lowest).
  • Associativity: Most operators are left-to-right associative, except^, which is right-to-left.
• Parentheses:
  • Push opening parentheses ( onto the stack.
  • Pop from the stack until you find a matching ) when encountering a closing parenthesis.

Step-by-Step Examples of Infix to Postfix Conversion

Example 01: 2 + 1

1. Operand 2 → Add to output: Output: 2
2. Operator + → Push to stack: Stack: +
3. Operand 1 → Add to output: Output: 2 1
4. End of expression → Pop stack: Output: 2 1 +

Postfix Result: 2 1 +

Example 02: 3 + 2 + 1

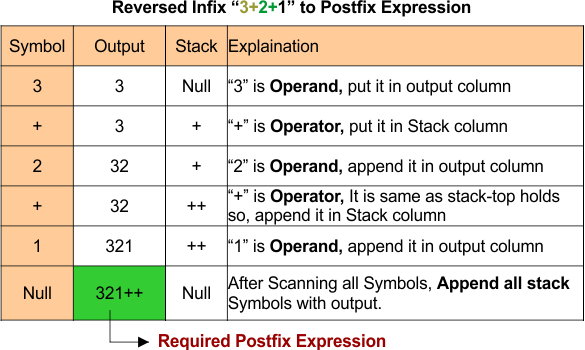
1. Operand 3 → Add to output: Output: 3
2. Operator + → Push to stack: Stack: +
3. Operand 2 → Add to output: Output: 3 2
4. Operator + → Push + to stack: Stack: ++
5. Operand 1 → Add to output: Output: 3 21 ++
6. End of expression → Pop stack: Output: 3 21++

Postfix Result: 3 21++

Example 03: 4 - 3 + 2 + 1

1. Operand 4 → Add to output: Output: 4
2. Operator - → Push to stack: Stack: -
3. Operand 3 → Add to output: Output: 4 3
4. Operator + → Pop - from stack (same precedence): Output: 4 3 - → Push +: Stack: +
5. Operand 2 → Add to output: Output: 4 3 - 2
6. Operator + → Output: 4 3 - 2 → Push +: Stack: ++
7. Operand 1 → Add to output: Output: 4 3 - 2 1
8. End of expression → Pop stack: Output: 4 3 - 2 1+ +

Postfix Result: 4 3 - 2 1++

Example 04: 1 - (2 + 3) * 4

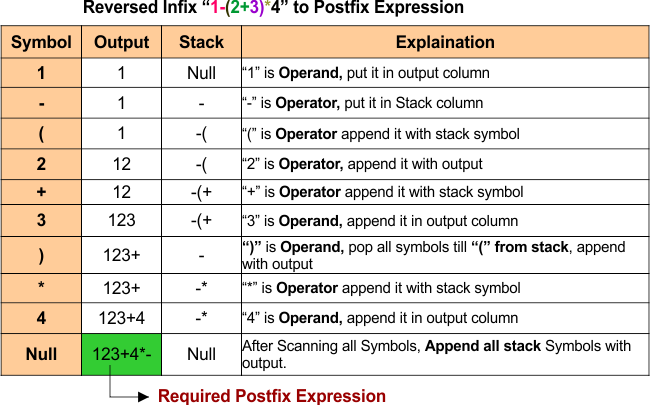
1. Operand 1 → Add to output: Output: 1
2. Operator - → Push to stack: Stack: -
3. ( → Push to stack: Stack: - (
4. Operand 2 → Add to output: Output: 1 2
5. Operator + → Push to stack: Stack: - ( +
6. Operand 3 → Add to output: Output: 1 2 3
7. ) → Pop stack until (: Output: 1 2 3 + → Remove (: Stack: -
8. Operator * → Push to stack: Stack: - *
9. Operand 4 → Add to output: Output: 1 2 3 + 4
10. End of expression → Pop stack: Output: 1 2 3 + 4 * -

Postfix Result: 1 2 3 + 4 * -

Example 05: (5 / 6) - (4 * (3 + 2))

1. ( → Push to stack: Stack: (
2. Operand 5 → Add to output: Output: 5
3. Operator / → Push to stack: Stack: ( /
4. Operand 6 → Add to output: Output: 5 6
5. ) → Pop stack until (: Output: 5 6 / → Remove (: Stack:
6. Operator - → Push to stack: Stack: -
7. ( → Push to stack: Stack: - (
8. Operand 4 → Add to output: Output: 5 6 / 4
9. Operator * → Push to stack: Stack: - ( *
10. ( → Push to stack: Stack: - ( * (
11. Operand 3 → Add to output: Output: 5 6 / 4 3
12. Operator + → Push to stack: Stack: - ( * ( +
13. Operand 2 → Add to output: Output: 5 6 / 4 3 2
14. ) → Pop stack until (: Output: 5 6 / 4 3 2 + → Remove (: Stack: - ( *
15. ) → Pop stack until (: Output: 5 6 / 4 3 2 + * → Remove (: Stack: -
16. End of expression → Pop stack: Output: 5 6 / 4 3 2 + * -

Postfix Result: 5 6 / 4 3 2 + * -

Benefits of Learning Infix to Postfix Conversion

• Simplifies Expression Evaluation: Postfix expressions can be evaluated using a simple stack algorithm.
• Optimized for Machines: No need to process parentheses or operator precedence.