Algorithm to Convert Infix to Postfix Using Stack
Converting an infix expression to postfix is a fundamental operation in data structures and algorithms. This process is crucial for simplifying expression evaluation in computer systems, particularly in compilers and calculators. In this article, we’ll explain the step-by-step algorithm to convert an infix expression to postfix using a stack, explain its working principles, and provide examples for a better understanding.
First understand the key difference in infix, prefix and postfix
| Feature | Infix | Postfix (Reverse Polish Notation – RPN) |
|---|---|---|
| Operator Placement | Between operands e.g., A+B | After operands e.g., AB+ |
| Parentheses Usage | Parentheses may used e.g., (A+B)×C | Not required; operator order determines precedence |
| Human Readability | Easy to understand and natural for humans | Less easy to understand for humans |
| Storage Efficiency | May require extra storage for parentheses | More compact; no need for parentheses |
| Algorithm Support | Needs algorithms like Shunting Yard for conversion | Easily evaluated using stack-based algorithms |
| Real-Life Use Cases | Human-written equations, programming expressions | Used in compilers, calculators, and interpreters |
Important: Prefix Notation (Polish Notation): Operators are placed before operands (e.g., +AB or ×+ABC). No need for parentheses; In prefix notation, evaluation occurs from right to left, while in postfix notation, it occurs from left to right.
Algorithm for Scanning Expression (Infix to Postfix)
The following algorithm provided is an implementation of the Shunting Yard Algorithm. It uses a stack-based approach to convert an infix expression to a postfix expression by systematically handling operands, operators, and parentheses based on their precedence and associativity. other methods are also available to convert infix to postfix as (Recursion-Based Approach, Manual Precedence Table). Let start leaning Shunting Yard Algorithm aproach
Step 01: Initialize:
- Create an empty stack.
- Start scanning the expression from left to right.
Step 02: For each symbol in the expression:
- If the symbol is an operand:
- Print that operand onto the screen.
- If the symbol is a left parenthesis
"("- Push it onto the stack.
- If the symbol is a right parenthesis
")"- Pop operators from the stack and print them onto the screen until a left parenthesis
(is encountered. - Discard both the left and right parentheses.
- Pop operators from the stack and print them onto the screen until a left parenthesis
- If the symbol is an operator:
- If the stack is not empty and the precedence of the operator on top of the stack is greater than or equal to the current operator:
- Pop the operators from the stack and print them onto the screen.
- Otherwise (else part): Push the current operator onto the stack.
- If the stack is not empty and the precedence of the operator on top of the stack is greater than or equal to the current operator:
Step 03: After scanning all the symbols:
- Pop and print any remaining operators from the stack.
Important: Precedence Rule: If the precedence of the operator on top of the stack is higher than or equal to the current operator, pop it. Otherwise, push the current operator onto the stack.
Algorithm Example to convert Infix to postfix: 7 + 5 * 3 / 5 ^ 1 + (3 - 2)
Let’s evaluate the expression 7 + 5 * 3 / 5 ^ 1 + (3 - 2) step by step using the stack method for converting an infix expression to postfix. I’ll also draw the diagrams at each step to illustrate how the stack is modified.
Important: you know about operator precedence before this class
Step 1: Initialize
- Create an empty stack.
- Start scanning from left to right.
Step 2: Scanning the infix expression
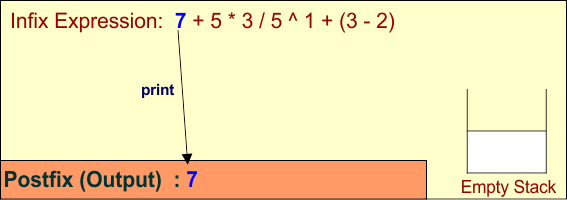
Symbol: 7
- Operand: Print
7.
Stack: (empty)
Output: 7
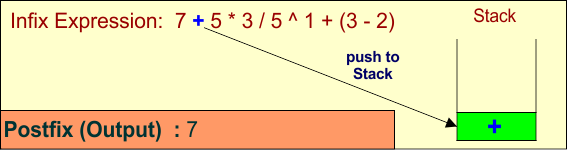
Symbol: +
- Operator: The stack is empty, so push
+onto the stack.
Stack: +
Output: 7
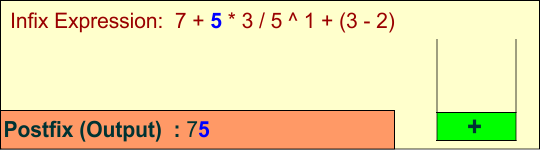
Symbol: 5
- Operand: Print
5.
Stack: +
Output: 7 5
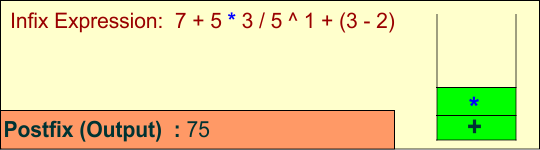
Symbol: *
- Operator: The stack contains
+, which has lower precedence than*. So, push*onto the stack.
Stack: + *
Output: 7 5
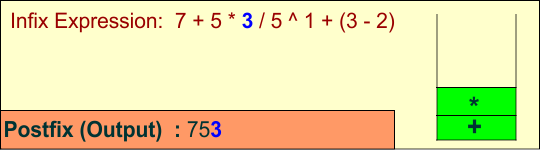
Symbol: 3
- Operand: Print
3.
Stack: + *
Output: 7 5 3
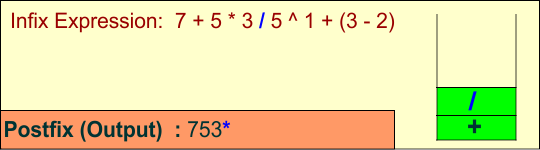
Symbol: /
- Operator: The top of the stack is
*, which has equal precedence to/, so pop*and print it. Then, push/onto the stack.
Stack: + /
Output: 7 5 3 *
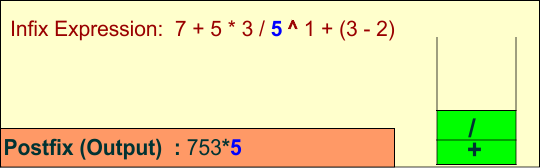
Symbol: 5
- Operand: Print
5.
Stack: + /
Output: 7 5 3 * 5
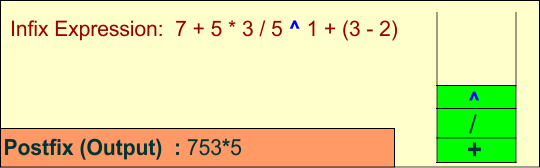
Symbol: ^
- Operator: The top of the stack is
/, which has lower precedence than^. So, push^onto the stack.
Stack: + / ^
Output: 7 5 3 * 5
Symbol: 1
- Operand: Print
1.
Stack: + / ^
Output: 7 5 3 * 5 1

Symbol: +
- Operator: The top of the stack is
^, which has higher precedence than+. So, pop^and print it. The next operator in the stack is/, which has higher precedence than+, so pop/and print it. Finally, push+onto the stack.
Note: if the same operator occurs as (+), push it into the stack over the previous +.
Stack: ++
Output: 7 5 3 * 5 1 ^ /

Symbol: (
- Left Parenthesis: Push it onto the stack.
Stack: + + (
Output: 7 5 3 * 5 1 ^ /

Symbol: 3
- Operand: Print
3.
Stack: + +(
Output: 7 5 3 * 5 1 ^ / 3

Symbol: -
- Operator: Push
-onto the stack
Stack: + +( -
Output: 7 5 3 * 5 1 ^ / 3

Symbol: 2
- Operand: Print
2.
Stack: + +( -
Output: 7 5 3 * 5 1 ^ / 3 2

Symbol: )
- Right Parenthesis: Pop and print the operator
-from the stack until encountering a left parenthesis. Discard the parenthesis.
Stack: ++
Output: 7 5 3 * 5 1 ^ / 3 2 -

Step 3: After scanning all symbols
- Pop and print any remaining operators from the stack. Pop
+and print it.
Stack: (empty)
Output: 7 5 3 * 5 1 ^ /3 2 - ++

Final Postfix Expression:
7 5 3 * 5 1 ^ / 3 2 - ++
Now, the final postfix expression is ready!
| Important: After evaluation, the output of any infix expression gives the same output for their prefix or postfix notation.
Given Infix Expression:
|













