Difference Between B and B+ Tree

Even though B tree and B+ tree are similar, they have key differences in how they store and access data, which affects their speed and efficiency in different situations. These differences make B-Trees better for some tasks and B+ Trees better for others.

B-Trees and B+ Trees are both special types of trees used in databases and file systems to store and manage large amounts of data efficiently. They help in quickly finding, inserting, and deleting data.

What is a B-Tree?

A B-Tree is a self-balancing search tree where nodes can have multiple children. It maintains sorted data and allows searches, insertions, and deletions in logarithmic time.

Characteristics of B-Tree

  • Each node contains multiple keys and child pointers.
  • Nodes have a minimum and maximum number of keys (determined by order m).
  • Internal nodes store both keys and data.
  • Searching requires traversing multiple levels.
  • Supports both sequential and direct access.

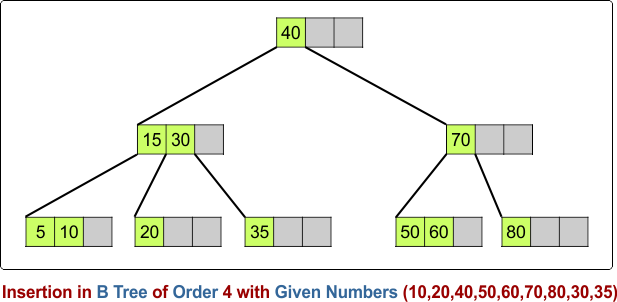
Example: B Tree of Order 4 with Given Numbers (10,20,40,50,60,70,80,30,35)

Insertion in B Tree of Order 4 with Given Numbers (10,20,40,50,60,70,80,30,35)

What is a B+ Tree?

A B+ Tree is an extension of the B-Tree that improves search performance by storing all data in leaf nodes. Internal nodes only store keys, serving as an index for faster lookups.

Characteristics of B+ Tree

  • Internal nodes contain only keys and act as an index.
  • All data is stored in leaf nodes.
  • Leaf nodes are linked, allowing fast sequential access.
  • Searching is more efficient due to uniform leaf storage.

Example: B+ Tree of Order 4 with Given Numbers (10,20,40,50,60,70,80,30,35)

Insertion in B+ Tree of Order 4 with Given Numbers (10,20,40,50,60,70,80,30,35)

Key Differences Between B Tree and B+ Tree

Let’s explain the major key differences in B and B+ trees in the data structure

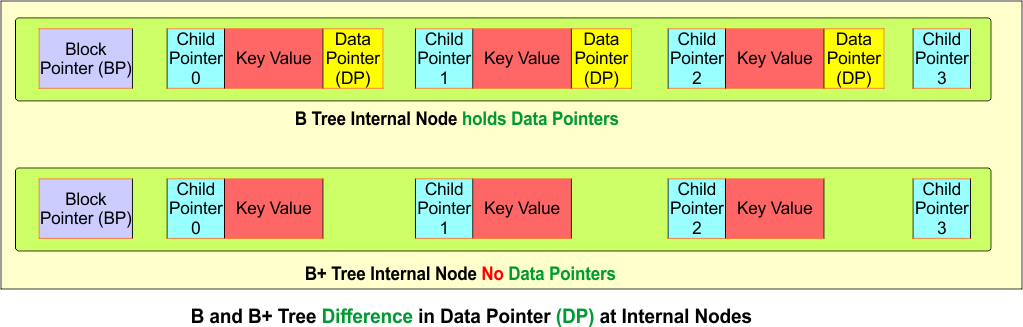
1.  No Data Pointer at Internal Nodes in B+ Tree

In B-Trees, internal nodes store both keys and data pointers (i.e., links to actual records or data).  In B+ Trees, internal nodes only store keys and do not contain data pointers. Data pointers are stored only in the leaf nodes.

B and B+ Tree Difference in Data Pointer (DP) at Internal Nodes

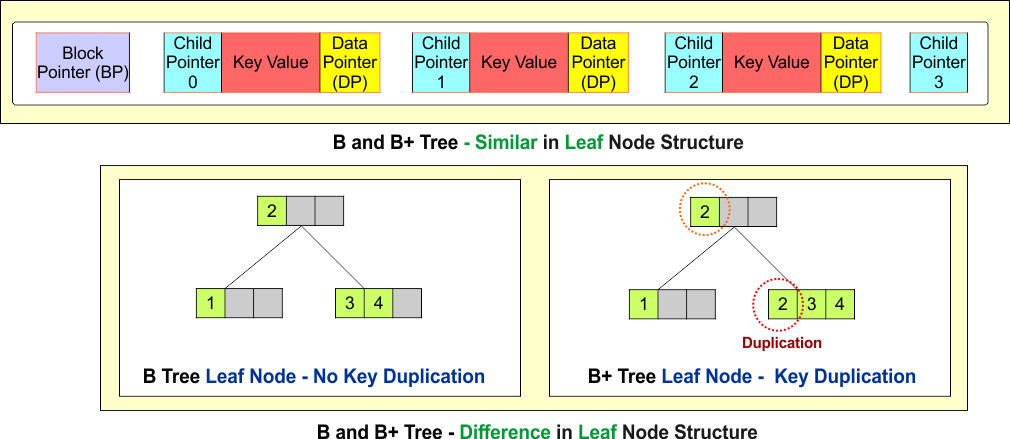
2. Key Duplication at Leaf Leaf Node in B+ Tree

In B-Trees, keys are stored in both internal nodes and leaf nodes, meaning there is no duplication. Each key appears only once in the tree, either in an internal node (along with data pointers) or in a leaf node.

In B+ Trees, keys from internal nodes must be repeated in the leaf nodes. Internal nodes store only keys (without associated data), while actual data is stored in leaf nodes.

B and B+ Tree - Difference and similarity in Leaf Node Structure

3. Finding Maximum Order (N)

Consider a case where

  • Memory block size = 4 KB (4096 bytes)
  • Key size = 16 bytes
  • Data pointer size = 8 bytes
  • Child Pointer size = 8 bytes
  • Order (fan-out) calculation formula:
    • B-tree: Each node contains keys + child pointers + data pointers
    • B+ tree: Internal nodes contain keys + child pointers, while leaf nodes contain keys + data pointers

Let’s explain

 I). B-Tree 

Each node in B-Tree consists of the following components:

  • N keys
  • N + 1 child pointers
  • N data pointers (since internal nodes store actual data)

Order calculation of B Tree is given in the following daigram

Finding Maximum N (N is order of B Tree) - For Each Node

So, the order of the B-tree is 127 (each internal node has up to 127 keys and 128 children).

 II). B+ Tree – For internal Node:

Each internal node contains:

  • N keys
  • N + 1 child pointers
  • No data Pointer

Order calculation of B Tree is given in the following diagram

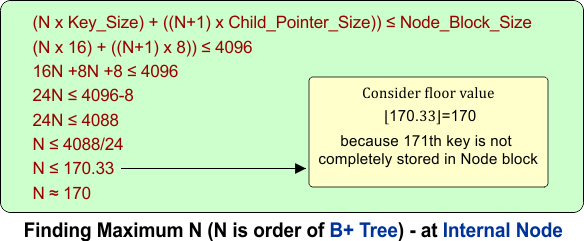
Finding Maximum N (N is order of B+ Tree) - at Internal Node

So, the order of the B+ tree internal node is 170 (each internal node has up to 170 keys and 171 children).

III).  B+ Tree – For Leaf Node:

Each Leaf node contains:

  • N keys
  • No child pointers
  • N data Pointers

Order calculation of B Tree is given in the following diagram

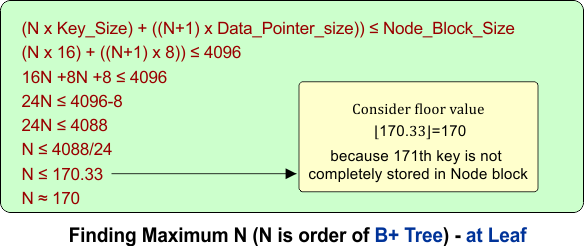
Finding Maximum N (N is order of B+ Tree) - at Leaf..

So, each leaf node stores 170 key-value pairs.

4. Extra Space Consumption in B Tree at Leaf

B tree: Even though leaf nodes do not have children, they still reserve space for child pointers, which are just set to NULL. This is because B-trees maintain a uniform structure where all nodes (both internal and leaf nodes) have child pointers to maintain consistency in the tree structure.

B+ tree: In leaf nodes of a B+ tree, child pointers are completely absent, not just set to null. This improves space utilization.

5. Height

The width of a tree increases with its order (m), because a higher order means each internal node can have more children. Since B+ trees have a higher m than B-trees, they are wider at each level.

B-Tree:

More keys per node → fewer levels.

B+ Tree

  • More keys per node due to no data in internal nodes.
  • Lower height for same number of nodes.

Proof: B+ Tree is shorter due to denser internal nodes.

6. Search Time

B-Tree

  • Searching can stop at internal nodes if data is found.
  • Example: Searching 30 stops at the root.
  • Disadvantage: Searching a key not in internal nodes takes longer.

B+ Tree

  • Search always reaches leaf nodes.
  • Example: Searching 30 requires reaching the leaf level.
  • Advantage: Faster search since all values are in leaf nodes.

Proof: The complexity is O(log n) in both trees, but in B+ Tree, the linked leaf structure allows sequential searches, making it faster in practice.

7. Insertion

B-Tree

  • Insertion can occur at any node (internal or leaf).
  • Requires splitting and restructuring.

B+ Tree

  • Always inserts at leaf nodes, reducing complexity.
  • Internal nodes are only updated when necessary.

Proof: O(log n) complexity in both, but B+ Tree always inserts at the leaf, making results predictable.

8. Deletion

B-Tree

  • Deleting an internal node requires complex restructuring.

B+ Tree

  • Deletion only happens at leaf nodes.
  • Internal keys are adjusted without affecting the structure.

Proof: Deletion in B+ Tree is easier because internal nodes only store indexes.

9. Sequential Access

B-Tree

  • Traversing in order requires recursion.
  • No linked list between leaf nodes.
  • Random access only.

B+ Tree

  • Linked leaf nodes allow efficient sequential access.
  • Leaf nodes are linked in a doubly linked list.
  • Supports faster range queries.

Proof: O(n) traversal in B-Tree vs. O(1) next access in B+ Tree.

10. Number of Nodes

  • A B+ Tree has more nodes than a B-Tree because internal nodes only store keys for navigation, while all actual data is stored in the leaf nodes.
  • In contrast, a B-Tree stores both keys and values in internal nodes, reducing the total number of nodes.

Simply, B-Trees are good for general indexing where data retrieval is needed at multiple levels. B+ Trees are better for large databases and file systems where fast sequential access and range queries are required.