Infix to Prefix Examples
In this class, we will learn infix to prefix examples involving very basic to advanced-level examples. Let’s start with a very basic example
Example 01: A + B
Step 1: Reverse the Infix Expression
The original infix expression A + B can be reversed to B + A, which switches the order of operands while retaining the operator.

Step 2: Scanning the Reversed Infix Expression
We scan each symbol of the reversed infix expression B + A. The operands B and A are printed directly, forming the output B A. The operator + is pushed onto the stack. At the end of the expression, the remaining operator is popped from the stack and appended to the output, resulting in the final postfix expression B A +.

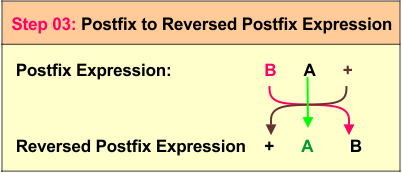
Step 3: Reverse the Postfix Expression
Finally, we reverse the postfix expression B A + to obtain the prefix expression + A B. This is the required final prefix expression.
Example 02: A + B + C
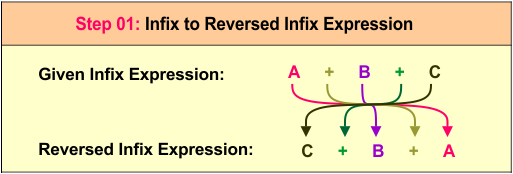
Step 1: Reverse the Infix Expression
The original infix expression A + B + C can be reversed to C + B + A, which maintains the same structure but changes the order of operands and operators.
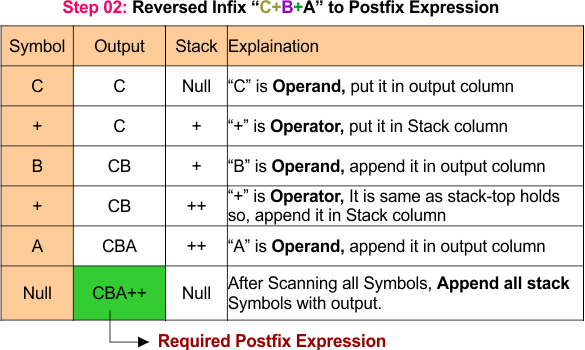
Step 2: Scanning the Reversed Infix Expression
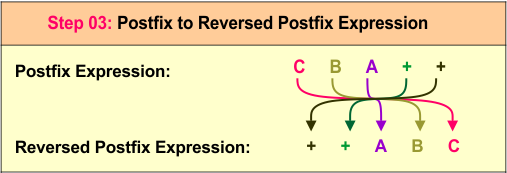
In a second step we will scan all symbols of reversed infix expressions. Operands C, B, and A are printed directly, by forming the output C B A. Operators are pushed onto the stack, with the first + added, followed by the second +. At the end of the expression, the remaining operators are popped and appended to the output, resulting in the final postfix expression C B A++. Following diagram explain it in detail
Step 3: Reverse the Postfix Expression
The postfix expression CBA++ reverses to the prefix expression ++ABC.
Example 03: A + B + C - D
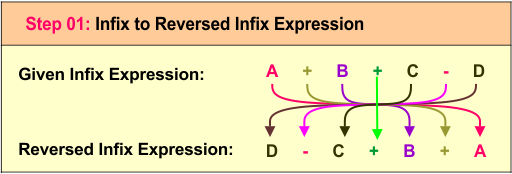
Step 1: Reverse the Infix Expression
The original infix expression A + B + C - D can be reversed to D - C + B + A, which changes the order of operands and operators while keeping the basic structure intact.
Step 2: Scanning the Reversed Infix Expression
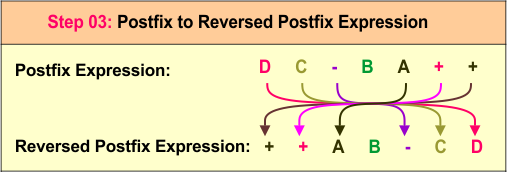
In this step, we scan each symbol of the reversed infix expression D - C + B + A. The operands D, C, B, and A are printed directly, forming the output D C B A. The operators - and + are pushed onto the stack, with the first - added, followed by the second +. At the end of the expression, we pop the remaining operators from the stack and append them to the output, resulting in the final postfix expression D C - B A + +. Order of execution is explain the following diagram

Important:When the stack top contains an operator that matches the upcoming operator, it is simply appended to the stack. For example, if a
+is at the top and another+arrives, the stack will hold++.
Step 3: Reverse the Postfix Expression
Next, we reverse the postfix expression D C -B A + + to obtain the prefix expression ++A B-CD. This is the desired final prefix expression.
Example 04: A * (B + C) – D
Step 1: Reverse the Infix Expression
The original infix expression A * (B + C) - D can be reversed to D - (C + B) * A, altering the order of operands and operators while keeping the structure intact.

Step 2: Scanning the Reversed Infix Expression
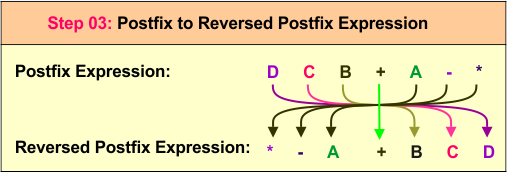
In this step, we scan each symbol of the reversed infix expression D - (C + B) * A. The operands D, C, B, and A are printed directly, forming the output D C B A. The operators -, +, and * are pushed onto the stack in sequence, with the first - added, followed by +, and *. At the end of the expression, the remaining operators are popped from the stack and appended to the output, resulting in the final postfix expression D C B A + * -.

Step 3: Reverse the Postfix Expression
Finally, we reverse the postfix expression D C B A + * - to obtain the prefix expression - * A + B C D. This is the desired final prefix expression.
Example 05: ((A + B) * C) – (D / E)
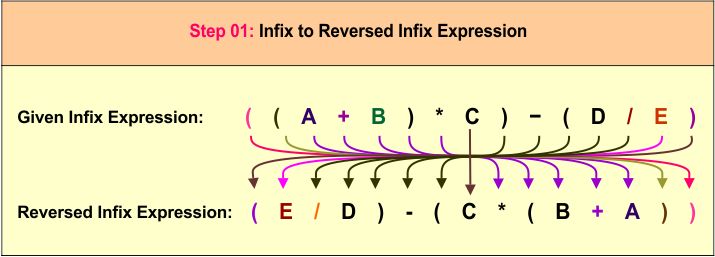
Step 1: Reverse the Infix Expression
The original infix expression ((A + B) * C) - (D / E) is reversed to (E / D) - (C * (B + A)), which changes the order of operands and operators while maintaining the overall structure.
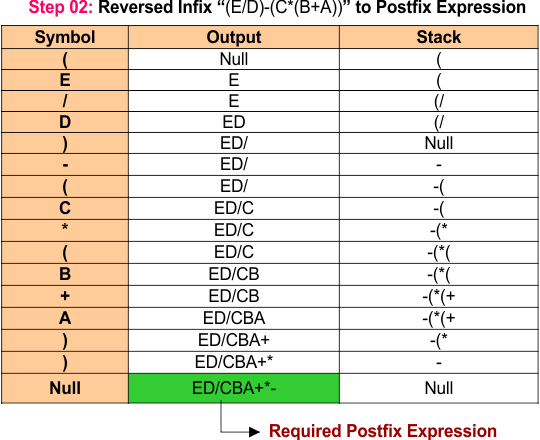
Step 2: Scanning the Reversed Infix Expression
Next, we scan each symbol of the reversed infix expression E / D - C * (B + A). The operands E, D, C, B, and A are printed directly, forming the output E D C B A. The operators /, -, *, and + are pushed onto the stack, with the first / added, followed by -, then *, and finally +. At the end of the expression, the remaining operators are popped from the stack and appended to the output, resulting in the final postfix expression E D / C B A + * -.
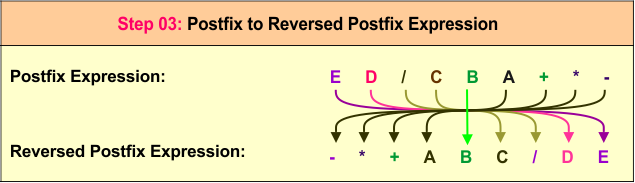
Step 3: Reverse the Postfix Expression
Finally, we reverse the postfix expression E D / C B A + * - to obtain the prefix expression - * C + B A / D E. This is the desired final prefix expression.