Binary Search Tree in Data Structure
In a binary search tree, the node has two types
- Leaf node: it contains no nodes (children).
- Non-leaf node: It contains one or two nodes. Non-leaf nodes are also called internal nodes.
Conditions for Binary Search Tree are given under
- The left sub-tree of a node contains only nodes with keys less than the nodes key.
- The right sub-tree of a node contains only nodes with keys higher than the nodes key.
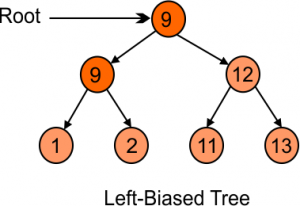
Note: If all equal elements are on left side then it is left biased tree. In the same case with right biased tree. But we can’t place equal number on left and right side in the same tree.
Example 01:
Create binary search tree (BST) with following Keys 4,2,3,6,5,7,1

Binary Number deletion
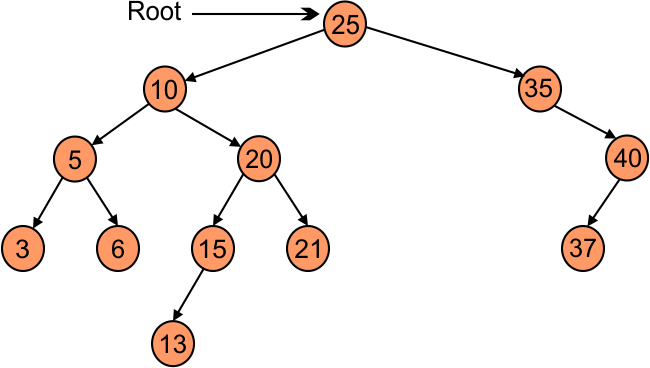
Consider the following diagram and explain all the cases of deletion
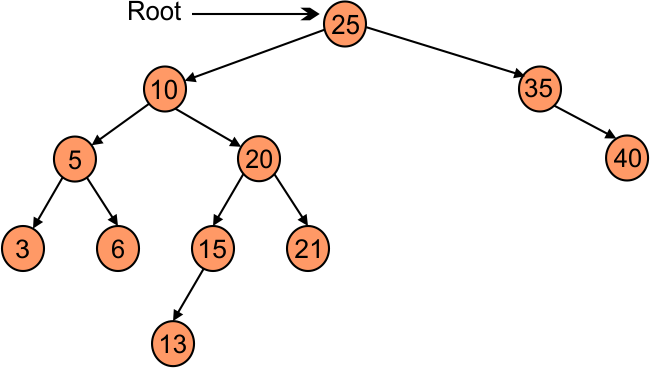
- Case 01: Leaf nod can simply delete without any problem. For example if we delete number 37 then binary tree will looks like the following,
- Case 02: If we delete a non-leaf node having single-node then attach the remaining one-node with the parent of deleted node. For example if we delete number 35 then binary tree will looks like the following way,
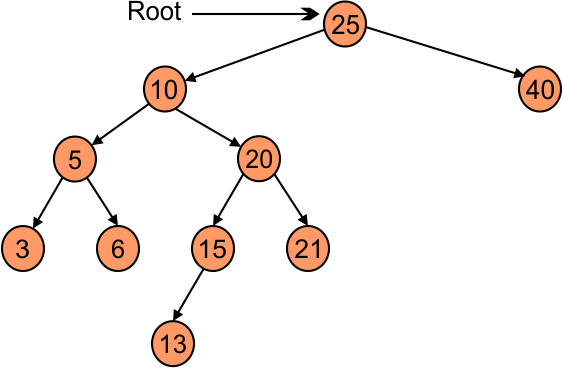
- Case 03: If we delete a non-leaf node having two-node then we can follow the following any cases from the following
Case 01: Go to left side of deleted node and find the largest number from the left side and replaced with deleted element. For example if we delete number 10 then,
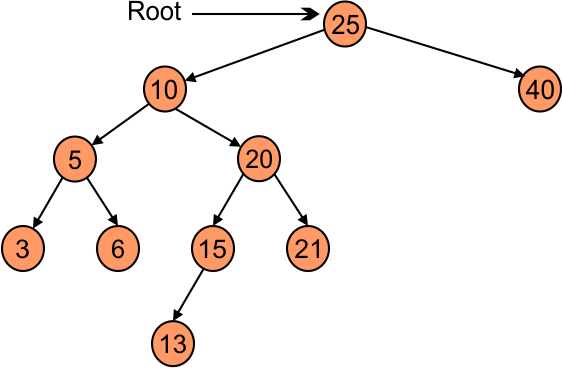
It is also called in order predecessors
Case 02: Go to right side of deleted node and find the lowest number from the right side and replaced with deleted element. For example if we delete number 10 then,
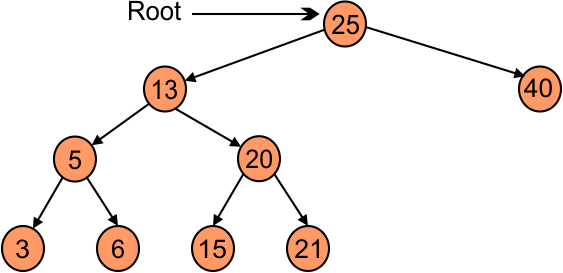
It is also called in order pre successors.
Problem in Binary Search Tree
Problem with binary search tree is left skewed and right skewed. In left skewed binary search tree there is no right child and in right skewed binary search tree all child nodes are on right side. As shown in the following diagram
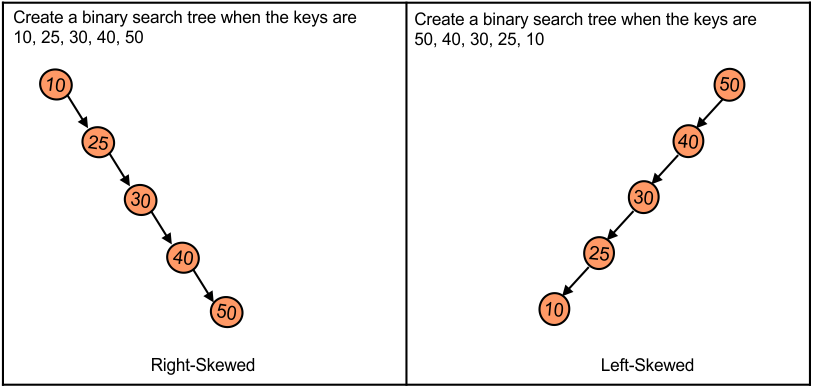
To resolve above problem we use ALV. ALV tree follow the balanced binary search tree.
Relation between Binary tree, binary search tree, and AVL is given below
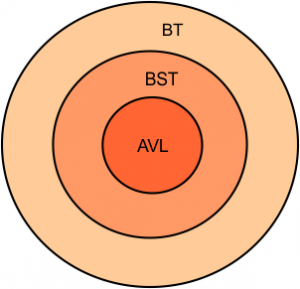
- Note: Every Binary tree (BT) is a Binary Search tree (BST) but not vice versa.
- Every ALV tree is a Binary search tree (BST) and Binary tree (BT) but not vice versa.
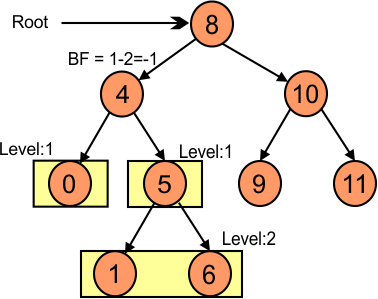
ALV Tree (Balance Factor)
- Balance factor should be -1, 0, or +1.
- Balance Factor (BF) = Height of left side tree (LST) – height of RST
Balance Factor of Root (8) in the following diagram is 1.
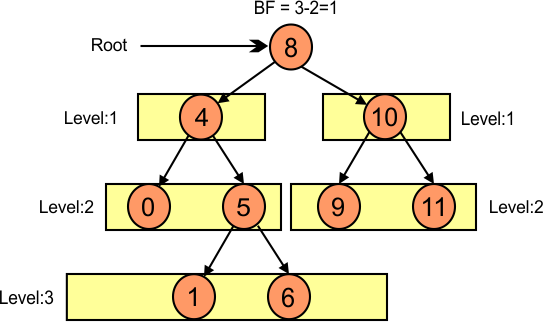
The balance factor of a node (4) in the following diagram is -1.