In large databases, searching for a record without an index requires scanning every record (O(N) complexity), which is slow
Indexing helps in
- Speeding up searches from O(N) to O(log N).
- Reducing disk I/O operations by efficiently locating data.
- Supporting fast insertions, deletions, and updates.
A B-Tree index is a self-balancing multi-way search tree designed for efficient disk-based searches.
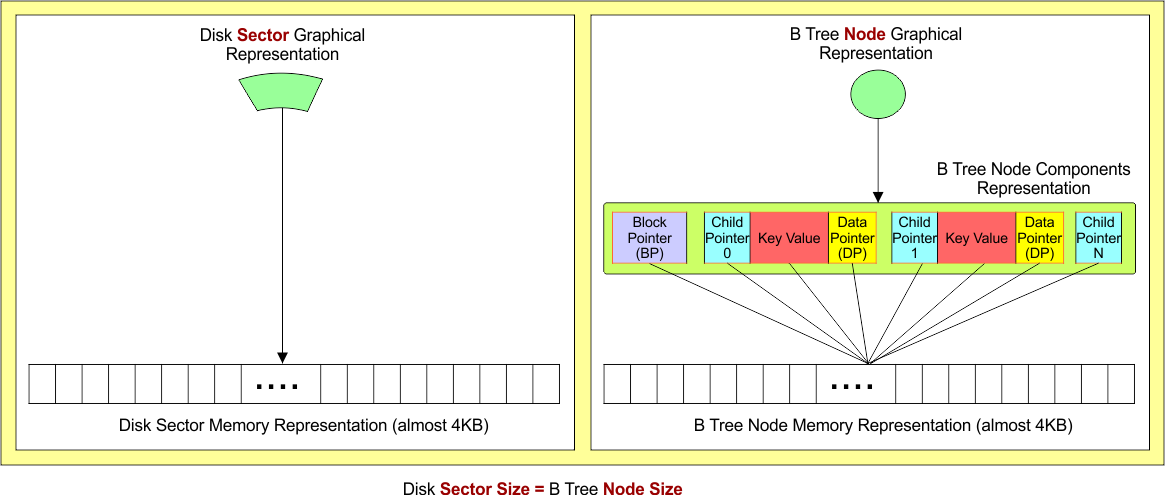
Disk-oriented trees (B-trees, B+ trees) are often designed with node sizes matching disk sector sizes to optimize I/O. Other trees (BST, AVL, Red-Black, Trie) do not follow this constraint and have variable node sizes based on dynamic memory allocation.
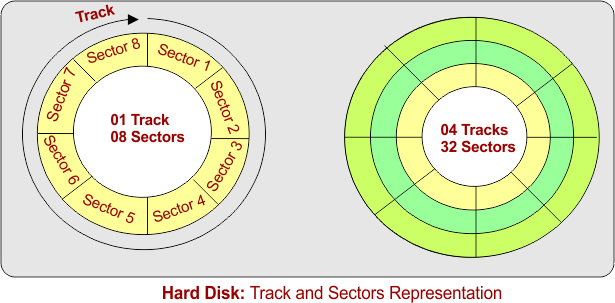
Before we proceed with the lecture, it is important to understand the structure of hard disks, particularly the concepts of tracks and sectors.
- Tracks → circles on a platter where data is stored.
- Sectors → A track is divided into small sections called sectors. A sector is the smallest unit of storage (typically 512 bytes or 4 KB).
Following is the representation of tracks and sectors on the hard disk
In database indexing using B-Trees, the node size is typically chosen to match the disk sector size. If the disk sector size = 4 KB, then the B-Tree node size is also chosen as 4 KB.
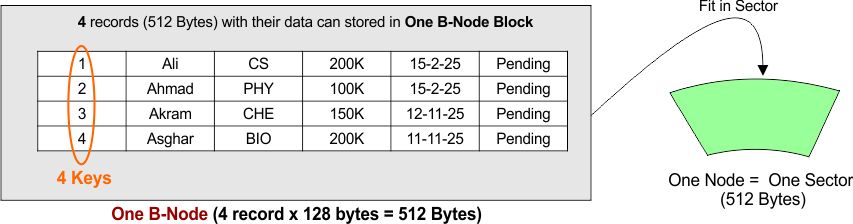
Example: Consider an Employe table with 100 records, where each record size is 128 bytes which is shown in the following diagram

following diagram shows how a record is fit into one sector of HD. As both B tree node and Hard disk sectors contains equal size so, it happened easily.
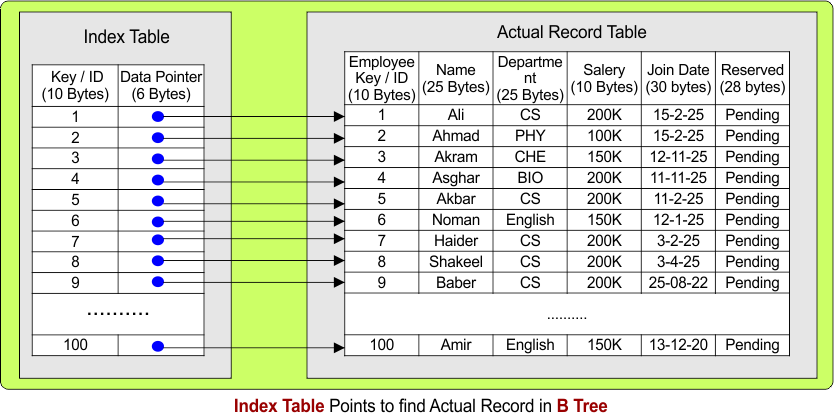
B tree node does not contains all record in a single node, it store only key and data pointer. Data pointer points to actual data in record table as shown in the following diagram.
How much time is required to access the required record in the given data of 100 Entries, Calculations are given below

Here is the problem with access time, we need at least 05 sectors to access (worst case) the required record out of 100 entries

How much time is required to access the required record in the given data of 1000 Entries, Calculations are given below
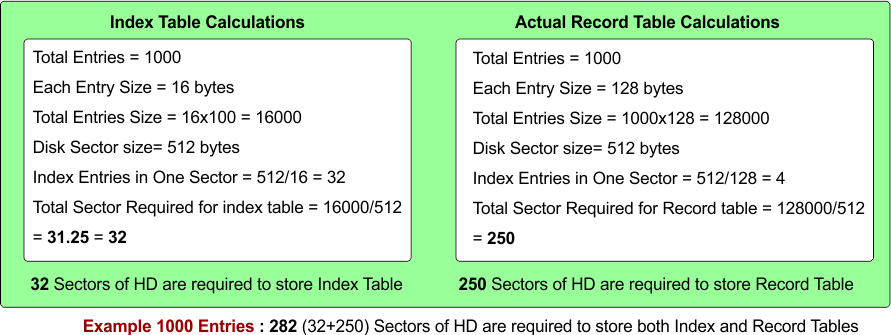
Here is the problem with access time, we need at least 33 sectors to access (worst case) the required record out of 1000 entries

Solution: Multilevel indexing, Resolve too many sectors access problem. Increasing the index level will reduce access time. As records increase, higher levels automatically form, making it a multi-level index without extra effort.

Search begins at the Outer Index, determining the relevant Inner Index. The Inner Index points to the correct disk block. The disk block is fetched, and the record is retrieved.
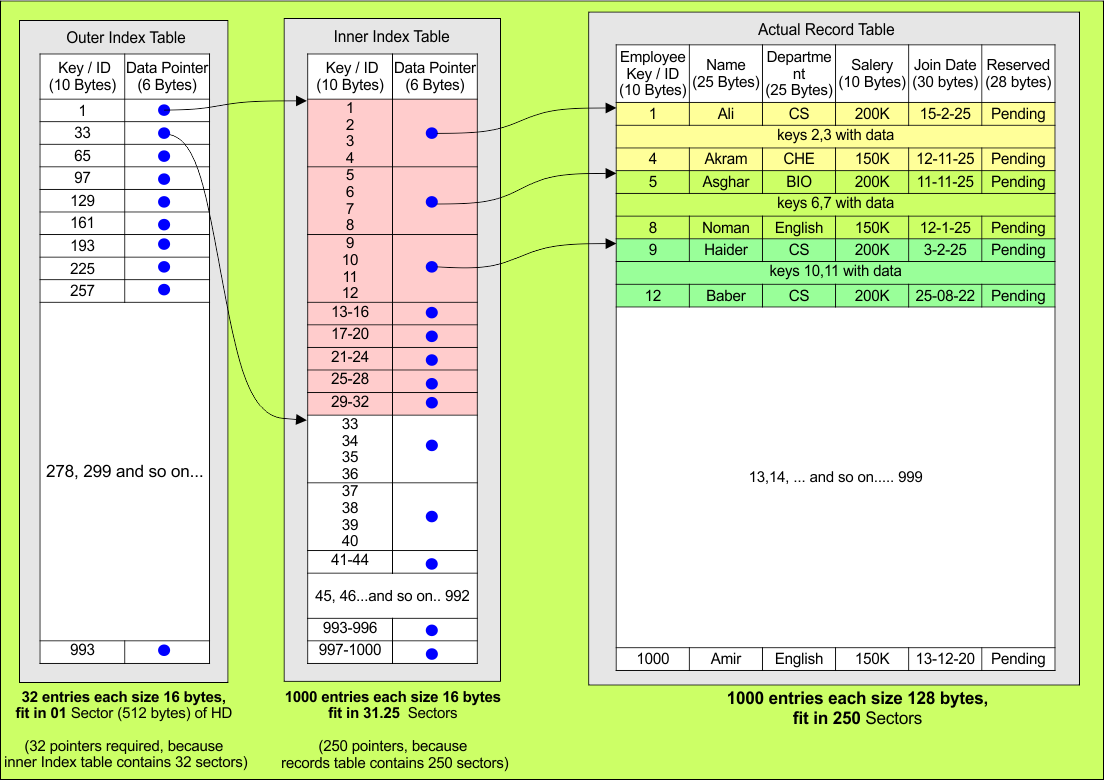
Important:
|













