Bankers Algorithm
Banker’s Algorithm is a deadlock avoidance strategy used in operating systems to ensure a safe state for resource allocation. It checks whether a system will remain in a safe state before allocating resources to a process. The algorithm works similarly to a banker who checks if granting a loan is safe before approving it—hence the name.
Why Banker’s Algorithm is Important?
Banker’s Algorithm helps:
- Avoid deadlock by checking future states
- Ensure resource utilization without risk
- Maintain system stability with multiple processes and limited resources
Key Terms in Banker’s Algorithm
Key terms in banker algorithm are given below
- Available: It indicates how many instances of each resource are currently free. Used to decide whether a process request can be safely granted.
- Max: The matrix that shows the maximum demand of each process. It defines how many resources each process may request to finish.
- Allocation: This matrix shows the current allocation of resources to each process. It tracks how much of each resource is already in use.
- Need: Calculated as Need = Max – Allocation. It shows how many more resources each process still requires to complete.
- Safe State: A system state where all processes can finish one by one without deadlock. There exists at least one safe sequence for execution.
- Unsafe State: A state where the system might enter a deadlock if resources are allocated. It doesn’t guarantee deadlock, but there is no safe sequence.
- Bankers Algorithm Formulas
Resource Vs Instance: Real Life Example
- Resource: A resource is a type or category of item that processes need to perform tasks.
- Instance: An instance is one unit of a resource. A single usable copy of that resource.
Example Scenario: In a cricket training camp, there are 3 players (processes) and 3 types of cricket equipment (resources):
| Equipment (Resource) | Total Instances |
|---|---|
| Bats (R1) | 7 bats |
| Balls (R2) | 9 balls |
| Helmets (R3) | 3 helmets |
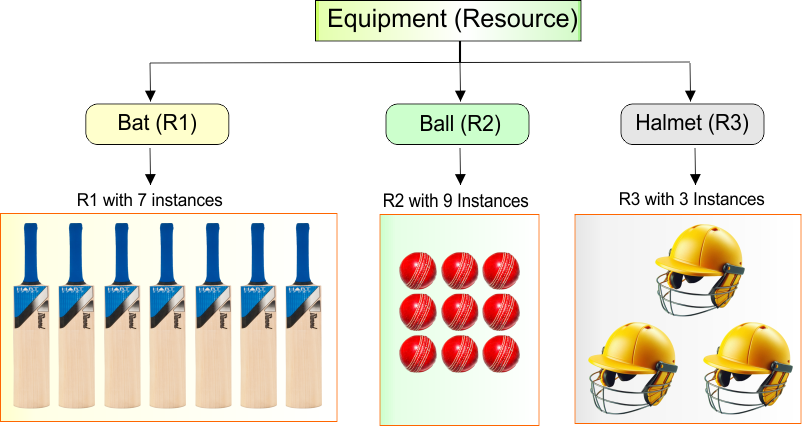
Each player needs some equipment to practice. The training manager uses the Banker’s Algorithm to avoid deadlock while distributing equipment.
Formulas in Banker Algorithm
Formula 01: Total Allocated Instance of Resource = Sum of Allocated Instances by all Processes
- Example: Total Allocated Instance of R1 = P1 Allocated Instance of R1 + P2 Allocated Instance of R1 + ….. PN
Formula 02: Maximum Need = Allocated Instances + Remaining Need
Derived from formula 01: If you’re given any 2 out of the 3 values, then you can always calculate the third using simple math
- Allocated Instances = Maximum Need – Remaining Need
- Remaining Need = Maximum Need – Allocated Instances
Formula 03: Total Instance = Allocated Instance + Available Instance
Derived from formula 02: If you’re given any 2 out of the 3 values, then you can always calculate the third using simple math
- Allocated Instance = Total Instance – Available Instance
- Available Instance = Total Instance – Allocated Instance
Formula 04: Need Instance ≤ Available Instance
- Need Instance is calculated from formula 01.
- Available Instance is calculated from formula 02.
- Formula 4 is a base condition for process execution.
Formula 05: Available Instance = Available Instance + Allocated Instance (of the completed process)
- It is used when a process completes, it releases its allocated resources.
Working of Bankers Algorithm
The first three formulas are used only once, when we try to solve the banker’s algorithm.
- Total Allocated Instance of Resource = Sum of Allocated Instances by all Processes
- Maximum Need = Allocated Instances + Remaining Need
- Total Instance = Allocated Instance + Available Instance
4th and 5th formulas are repeated in sequence (3rd first, 4th later) until all processes are executed or checked for their execution
- Need Instance ≤ Available Instance
- Available Instance = Available Instance + Allocated Instance (of the completed process)A
Working Flow chart of Banker’s Algorithm is given below

Let’s understand the banker’s algorithm with an example
Banker’s Algorithm Example 01:
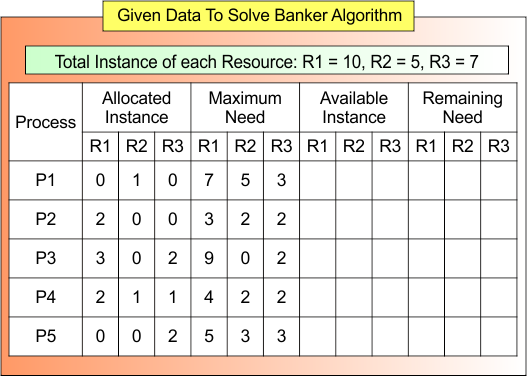
Given values of the Banker’s Algorithm are
- Total Instance
- Allocated instance
- Maximum Need
We have to find
- Total Allocated Instance
- Available Instance
- Remaining Need
- Safe Sequence
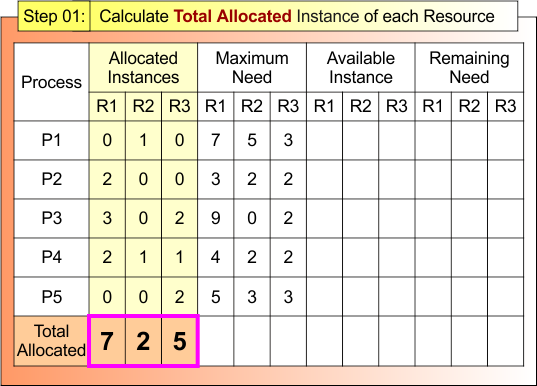
Step 01 – Calculate the Total Allocated Instance of each Resource
According to formula 01: Total Allocated Instance of Resource = Sum of Allocated Instances by all Processes
- Total Allocated to R1 = 0+2+3+2+0 = 7
- Total Allocated to R2 = 1+0+0+1+0 = 2
- Total Allocated to R3 = 0+0+2+1+2 = 5
Step 01 result is updated in the following Banker Table
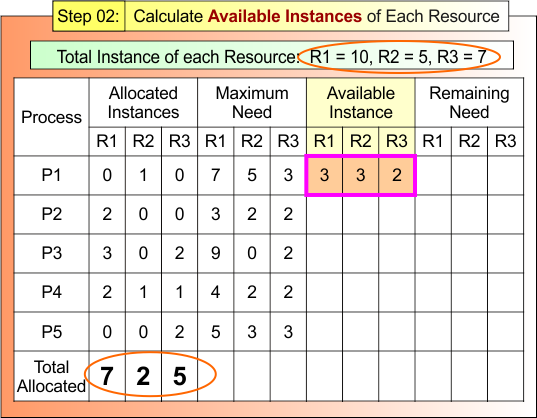
Step 02: Calculate Available Instances of Each Resource
According to formula 02:
Available Instances = Total Instances – Total Allocated
R1 Available Instances = 10 – 7 = 3
R2 Available Instances = 5 – 2 = 3
R3 Available Instances = 7 – 5 = 2
Step 02 result is updated in the following Banker Table
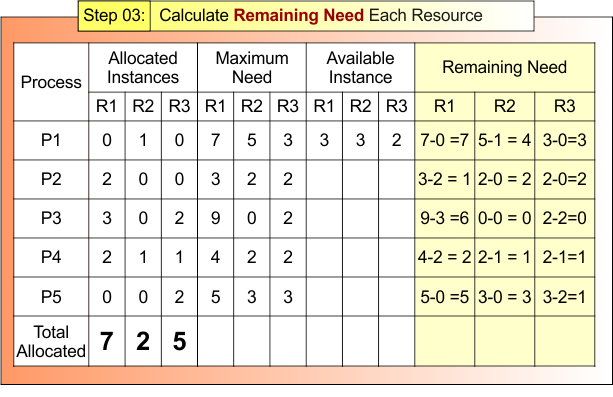
Step 03: Calculate Remaining Need for Each Resource
According to Formula 03
Remaining Need = Maximum Need – Allocated Instances
- Remaining Need R1 = Maximum Need R1 – Allocated Instances R1
- Remaining Need R2 = Maximum Need R2 – Allocated Instances R2
- Remaining Need R3 = Maximum Need R3 – Allocated Instances R3
Step 03 result is updated in the following Banker Table
Step 04: Check Process Execution One by One
According to formula 04
Process Execution Formula = Remaining Need ≤ Available Instance
For Process P1
- Remaining Need = (7, 4, 3)
- Available = (3, 3, 2)
- Remaining Need <=Available = False
System moves to Next Process (P2)
For Process P2
- Remaining Need = (1, 2, 2)
- Available = (3, 3, 2)
- Remaining Need <=Available = True
Process P2 Get Executed and Release Its Allocated Instances (2,0,0).
According to formula 05
Available Instance = Available (3, 3, 2) + Release (2,0,0)
= (3+2+3) + (0+2+0)
= (5, 3, 2)
Step 04 result is updated in the following Banker Table
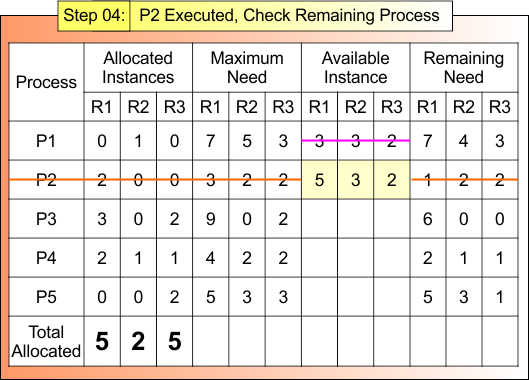
Safe Sequence Starts with Process P2
| Note: Formulas 04 and 05 are repeated until all processes are executed or check for their execution |
Step 4.1: P2 Executed, Check Remaining Process
After Step 04
- Process P2 is Terminated
- Available Instances (5,3,2)
Now,
For Process P3
- Remaining Need = (6, 0, 0)
- Available = (5, 3, 2)
- Remaining Need <=Available = False
For Process P4
- Remaining Need = (2, 1, 1)
- Available = (5, 3, 2)
- Remaining Need <=Available = True
Process P4 Get Executed and Release Its Allocated Instances (2,1,1).
Available Instance = Available (5, 3, 2) + Release (2,1,1)
= (5+3+2) + (2+1+1)
= (7, 4, 3)
Step 4.1 result is updated in the following Banker Table
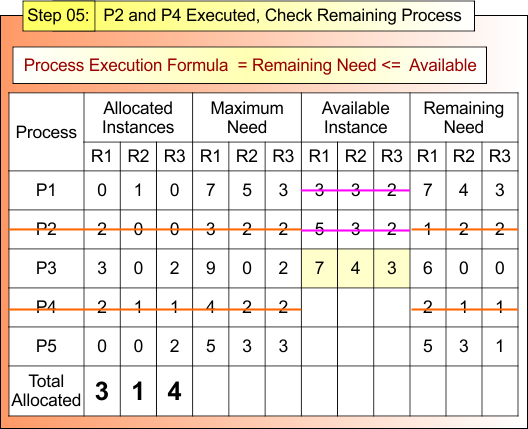
Safe Sequence P2 → P4
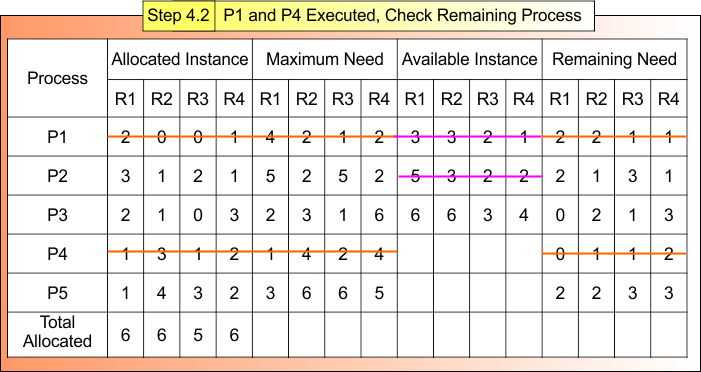
Step 4.2: P2 and P4 Executed, Check Remaining Process
After Step 4.1
- Process P2 and P4, Terminated
- Available Instances (7,4,3)
Now,
For Process P5
- Remaining Need = (5, 3, 1)
- Available = (7, 4, 3)
- Remaining Need <= Available = True
Process P5 Get Executed and Release Its Allocated Instances (0,0,2).
Available Instance = Available (7, 4, 3) + Release (0,0,2)
= (7+4+3) + (0+0+2)
= (7, 4, 5)
Step 4.2 result is updated in the following Banker Table
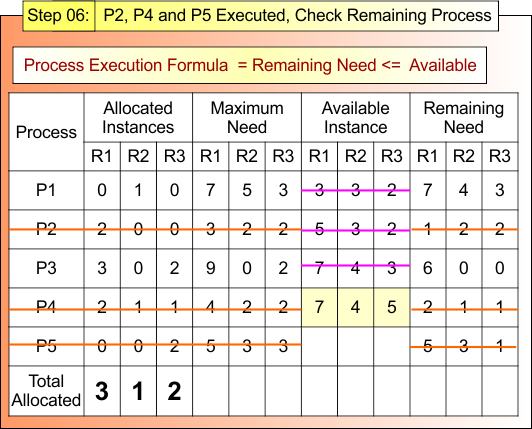
Safe Sequence P2 → P4 → P5
Step 4.3: P2, P4 and P5 Executed, Check Remaining Process
After Step 4.2
- Process PP2, P4 and P5 are Terminated
- Available Instances (7,4,5)
Now,
For Process P1
- Remaining Need = (7, 4, 3)
- Available = (7, 4, 5)
- Remaining Need <= Available = True
Process P1 Get Executed and Release Its Allocated Instances (0,1,0).
Available Instance = Available (7, 4, 5) + Release (0,1,0)
= (7+4+5) + (0+1+0)
= (7, 5, 5)
Step 4.3 result is updated in the following Banker Table
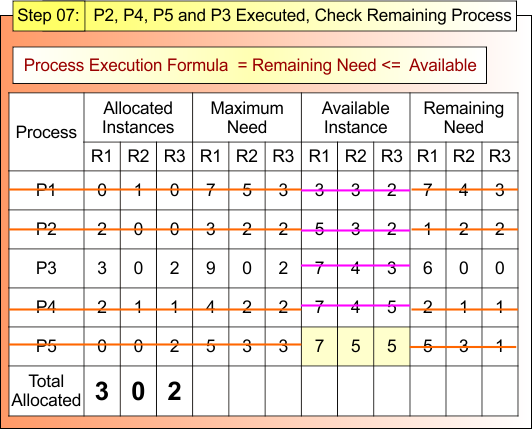
Safe Sequence: P2 → P4 → P5 → P1
Step 4.4 : P2, P4, P5 and P3 Executed, Check Remaining Process
After Step 4.3
- Process P2, P4, P5 and P3 are Terminated
- Available Instances (7,5,5)
Now,
For Process P3
- Remaining Need = (6, 0, 0)
- Available = (7, 5, 5)
- Remaining Need <= Available = True
Process P3 Get Executed and Release Its Allocated Instances (3,0,2).
Available Instance = Available (7, 5, 5) + Release (3,0,2)
= (7+5+5) + (3+0+2)
= (10, 5, 7)
All Process (P1, P2, P3, P4 and P5) are Executed . Step 4.4 result is updated in the following Banker Table
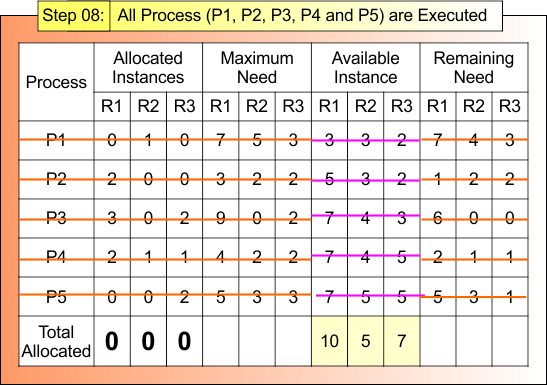
Safe Sequence: P2 → P4 → P5 → P1 → P3
If all processes are executed, then
- A safe sequence must exist
- Total allocated resources will be zero
- Total Instances of each resource = Available resources
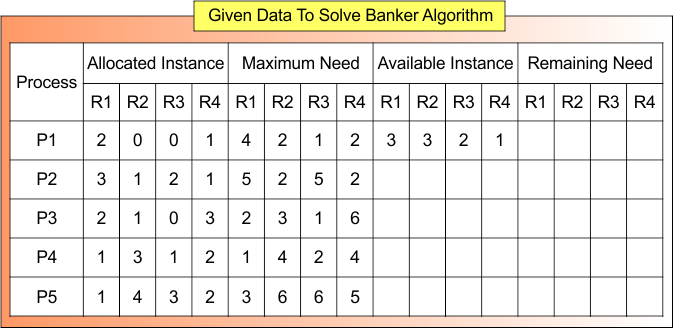
Example 02: Banker Algorithm
Given values of the Banker’s Algorithm are
- Allocated instance
- Maximum Need
- Available Instance
We have to find
- Total Instance
- Total Allocated Instance
- Remaining Need
- Safe Sequence
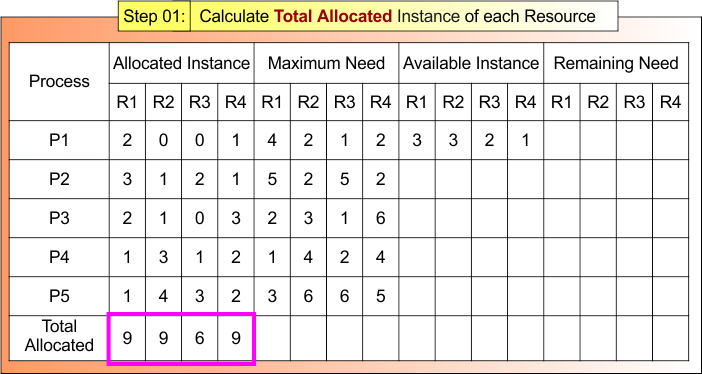
Step 01 – Calculate the Total Allocated Instance of each Resource
According to formula 01: Total Allocated Instance of Resource = Sum of Allocated Instances by all Processes
- Total Allocated to R1 = 2+3+2+1+1 = 9
- Total Allocated to R2 = 0+1+1+3+4 = 9
- Total Allocated to R3 = 0+2+0+1+3 = 6
- Total Allocated to R4 = 1+1+3+2+2 = 9
Step 01 result is updated in the following Banker Table
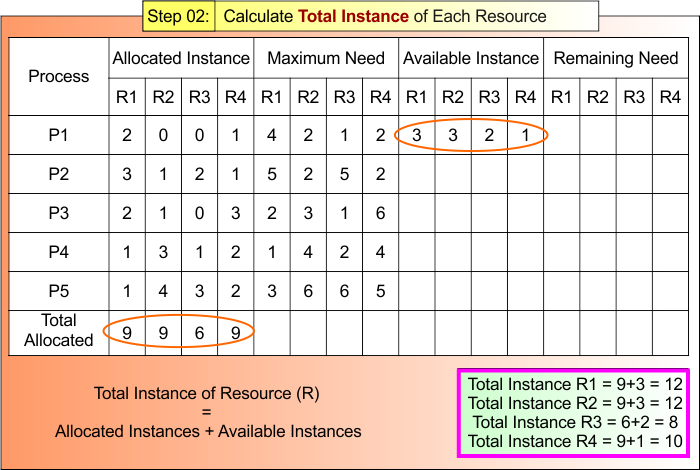
Step 02: Calculate Total Instances of Each Resource
According to formula 02:\
Total Instance of Resource (R) = Allocated Instances + Available Instances
- R1 Total Instances = 9 – 3 = 12
- R2 Total Instances = 9 + 3 = 12
- R3 Total Instances = 6 + 2 = 8
- R3 Total Instances = 9 + 1= 10
Step 02 result is updated in the following Banker Table
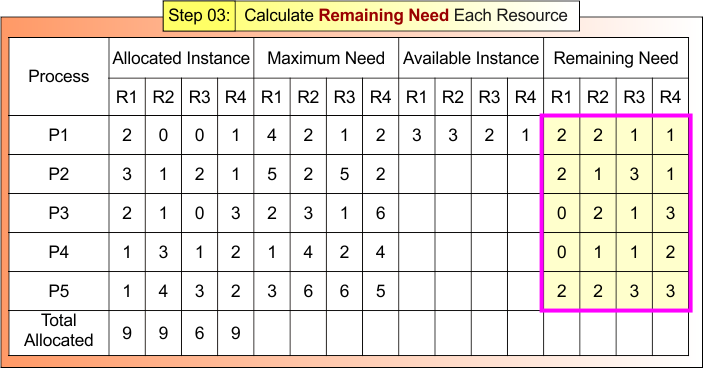
Step 03: Calculate Remaining Need for Each Resource
According to Formula 03
Remaining Need = Maximum Need – Allocated Instances
- Remaining Need R1 = Maximum Need R1 – Allocated Instances R1
- Remaining Need R2 = Maximum Need R2 – Allocated Instances R2
- Remaining Need R3 = Maximum Need R3 – Allocated Instances R3
- Remaining Need R4 = Maximum Need R4 – Allocated Instances R4
Step 03 result is updated in the following Banker Table
Step 04: Check Process Execution One by One
Now we have the following information
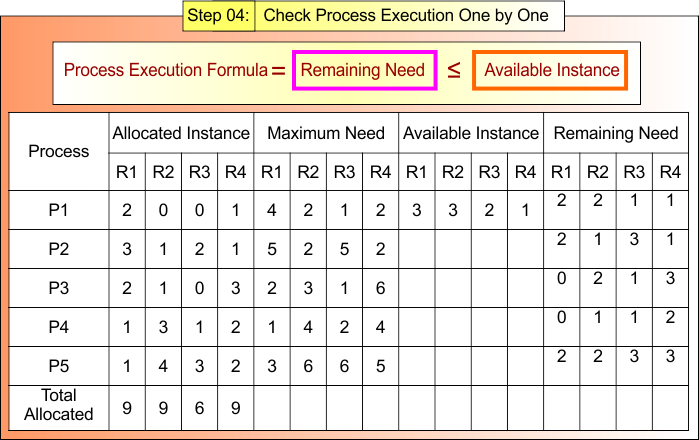
Check Process Execution One by One by using formula 04
Process Execution Formula = Remaining Need ≤ Available Instance
Step 4.1: Check First Process Execution
For Process P1
- Remaining Need = (2, 2, 1,1)
- Available = (3, 3, 2,1)
- Remaining Need ≤ Available = True
Process P1 Get Executed and Release Its Allocated Instances (2,0,0,1).
According to formula 05
Available Instance = Available (3, 3, 2,1) + Release (2,0,0,1)
= (3+3+2+1) + (2+0+0+1)
= (5, 3, 2,2)
Step 4.1 result is updated in the following Banker Table
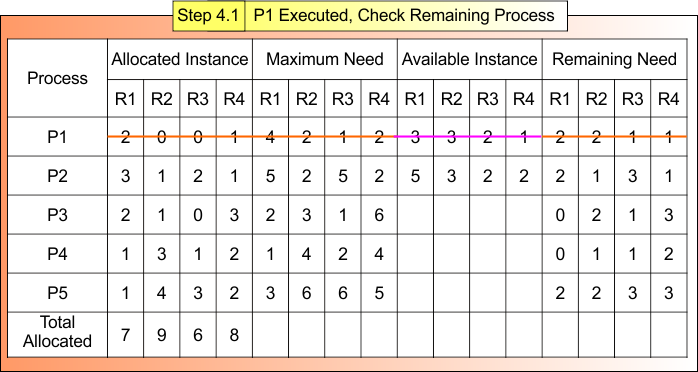
Safe Sequence Starts with Process P1
| Note: Formulas 04 and 05 are repeated until all processes are executed or check for their execution |
Step 4.2: P1 Executed, Check Remaining Process
After Step 4.1
- Process P1 is Terminated
- Available Instances (5,3,2,2)
Now,
For Process P3
- Remaining Need = (0, 2, 1, 3)
- Available = (5, 3, 2, 2)
- Remaining Need <=Available = False
For Process P4
- Remaining Need = (0, 1, 1, 2)
- Available = (5, 3, 2, 2)
- Remaining Need <=Available = True
Process P4 Get Executed and Release Its Allocated Instances (1,3,1,2).
Available Instance = Available (5, 3, 2) + Release (2,1,1)
= (5, 3, 2, 2) + (1,3,1,2)
= (6, 6, 3, 4)
Step 4.2 result is updated in the following Banker Table
Safe Sequence P1 → P4
Step 4.3: P1 and P4 Executed, Check Remaining Process
After Step 4.2
- Process P1 and P4, Terminated
- Available Instances (6,6,3,4)
Now,
For Process P5
- Remaining Need = (2, 2, 3,3)
- Available = (6,6,3,4)
- Remaining Need <= Available = True
Process P5 Get Executed and Release Its Allocated Instances (1,4,3,2).
Available Instance = Available (6,6,3,4) + Release (1,4,3,2)
= (6,6,3,4) + (1,4,3,2)
= (7, 10, 6, 6)
Step 4.3 result is updated in the following Banker Table
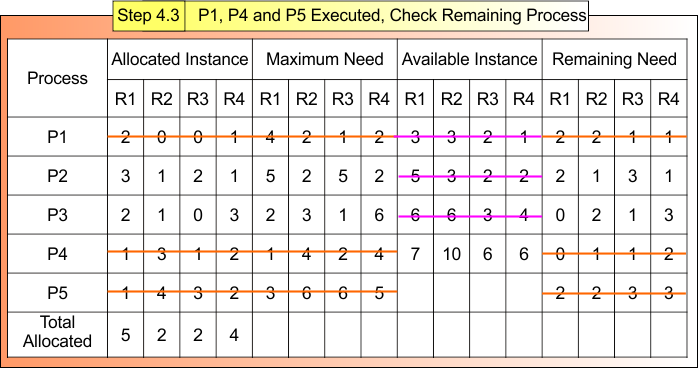
Safe Sequence P1 → P4 → P5
Step 4.4: P1, P4 and P5 Executed, Check Remaining Process
After Step 4.3
- Process P1, P4 and P5 are Terminated
- Available Instances (7,10,6,6)
Now,
For Process P2
- Remaining Need = (2, 1, 3,1)
- Available = (7,10,6,6)
- Remaining Need <= Available = True
Process P2 Get Executed and Release Its Allocated Instances (3, 1, 2,1).
Available Instance = Available (7,10,6,6) + Release (3, 1, 2,1)
= (7,10,6,6) + (3, 1, 2,1)
= (10, 11, 8,7)
Step 4.4 result is updated in the following Banker Table
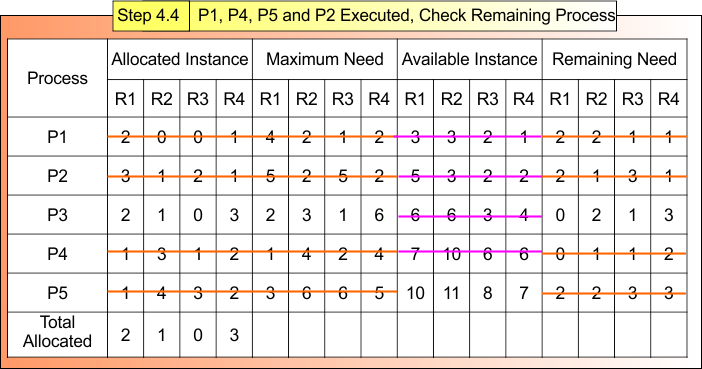
Safe Sequence: P1 → P4 → P5 → P2
Step 4.5 : P1, P4, P5 and P2 Executed, Check Remaining Process
After Step 4.4
- Process P1, P4, P5 and P2 are Terminated
- Available Instances (10,11,8,7)
Now,
For Process P3
- Remaining Need = (0, 2, 1, 3)
- Available = (10,11,8,7)
- Remaining Need <= Available = True
Process P3 Get Executed and Release Its Allocated Instances (2,1,0,3).
Available Instance = Available (10,11,8,7) + Release (2,1,0,3)
= (10,11,8,7) + (2,1,0,3)
= (12, 12, 8, 10)
All Process (P1, P2, P3, P4 and P5) are Executed . Step 4.5 result is updated in the following Banker Table
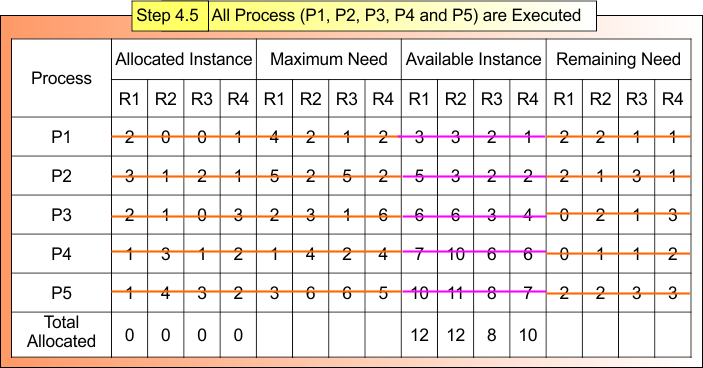
Safe Sequence: P1 → P4 → P5 → P2 → P3
If all processes are executed, then
- At least one safe sequence must exist (more than one safe sequence are possible)
- Total allocated resources will be zero
- Total Instances of each resource = Available resources
Example 03: Banker Algorithm
Given values of the Banker’s Algorithm are
- Allocated instance
- Maximum Need
- Available Instance
- Total Allocated Instance
- Remaining Need
Find system is in a safe state or an unsafe state.
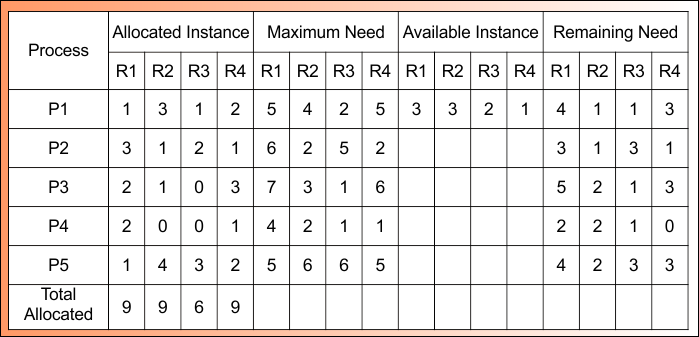
Check Process Execution One by One by using formula 04
Process Execution Formula = Remaining Need ≤ Available Instance
Process P1, P2, P3, and P5 cannot be executed. Only Process P4 can execute
For Process P4
- Remaining Need = (2, 0, 0,1)
- Available = (3, 3, 2,1)
- Remaining Need ≤ Available = True
Process P4 Get Executed and Release Its Allocated Instances (2,0,0,1).
According to formula 05
Available Instance = Available (3, 3, 2,1) + Release (2,0,0,1)
= (3+3+2+1) + (2+0+0+1)
= (5, 3, 2,2)
Step 4.1 result is updated in the following Banker Table
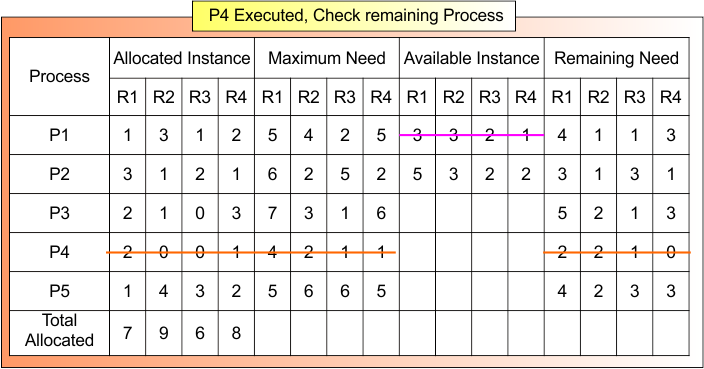
After P4 is completed, Available Instance = (5, 3, 2,2). following formula does not fulfill the conditions for Remaining all process (i.e. P1, P2, P3, P5).
- Remaining Need ≤ Available Instance
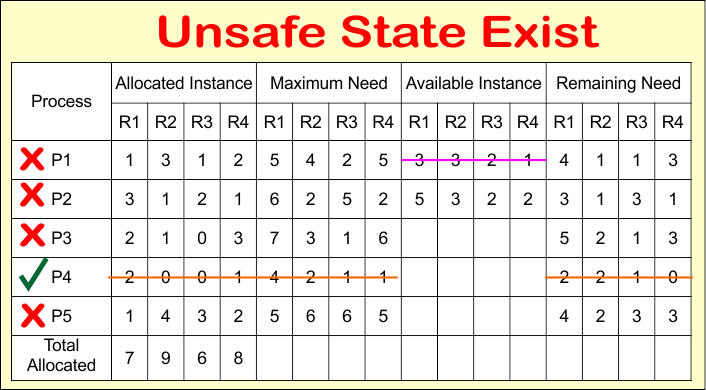
So, safe sequence does not found. It is called an unsafe state of the system
Advantages of Banker’s Algorithm
Here are the most important advantages of banker’s algorithms are given below
-
Avoids Deadlock: Only grants resource requests if the system will remain in a safe state.
-
Ensures Safe Execution: Guarantees that all processes can complete without entering deadlock.
-
Efficient Resource Management: Allocates resources only when it’s safe, avoiding waste and overuse.
-
Simulates Before Allocation: Uses a “what-if” approach to test safety before actually giving resources.
-
Supports Multiple Resource Types: Works well even when different types of resources have multiple instances.
-
Educational Value: A classic algorithm for teaching deadlock avoidance in operating systems.
-
Fair Allocation: Prevents starvation by checking system safety for all processes equally.
Disadvantages of Banker’s Algorithm
Here are the disadvantages of the Banker’s Algorithm
-
Requires Prior Knowledge of Maximum Resource Need: Each process must declare in advance how many resources it may need, not always possible in real-world applications.
-
High Computational Overhead: The system must perform safety checks every time a resource is requested, which increases CPU usage and slows down performance.
-
Not Scalable for Large Systems: In systems with many processes and resource types, the calculations become complex and inefficient.
-
Rigid and Inflexible: The algorithm is strict and doesn’t adapt well to dynamic environments where processes and needs change over time.
-
Assumes Honest Behavior: It assumes that processes will never ask for more than their declared maximum, which may not always be true.
-
Rarely Used in Practice: Due to its complexity and unrealistic assumptions, it is not used in real-world operating systems.













